Д.т.н. Джаббаров И.И., Джаббарова А.И., Гадиева С.С.,

Кулиева У.Р., д.т.н. Сафарли И.С.

Сумгаитский Государственный Университет, Азербайджан

ДВИЖЕНИЕ ЖИДКОСТИ В ТРЕХ ЗОНАЛЬНООДНОРОДНЫХ СРЕДАХ СО СЛАБОПРОНИЦАЕМЫХ КРОВЛЯМИ ПРИ ДЕЙСТВИИ В ЖИДКОЙ ИЗ ЗОН ПО ОДНОЙ СКВАЖИНЕ С ПОСТОЯННЫМ ДЕБИТОМ

В статье рассматривается неустановивщееся движение жидкости, подчиняющееся линейному закону фильтрации к совершенным скважином, распрележенным в бесконечном по простиранию пласте со слабопроницаемой кровлей. При решение задач был использован метод разделения переменных и интегральное преобразование Лапласа.

K₃

M₃

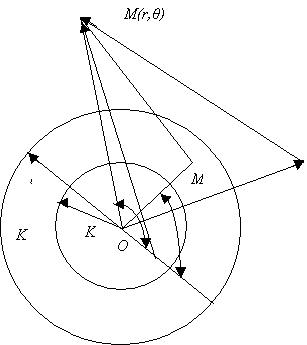
Предполагается, что разра-батываемый достаточно большой по построению пласт, разделен от вышележащего неразрабатывае-мого соседнего пласта, в котором поддерживается постоянного дав-ления через слабопроницаемую перемычку и в нем имеются две зоны в виде круга (зона I) и кольца (зона II), границами (рис.1), коэффициенты проницаемости и пъезопроводности зон I и II имеют различные постоянные значения, чем таковые остальной части пласта (зона III).

Схематическое изображение трех занольно-однородного нефтяного пласта действующий в при каждое с постоянный дебитами.

Скважины, пущенные в эксплуатацию с постоянными дебитами расположены в произ-вольных точках соответствующих зон пласта.

Эту задачу математически можно сформулировать следующим образом: найти решение следующей системы дифференциальных уравнений в частных производных, в которой учтены непроницаемость подошвы и слабопроницаемость кровля пласта

(1)

где – номера зон.

При следующих начальных и граничных условиях:

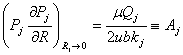(2)

при (3)

при (4)

при (5)

– цилиндрические координаты, – координаты точек в которых помещена скважины; –коэффициенты проницаемости и пъезопроводности -ой зоны; –коэффициент проницаемости перемычки; –коэффициент вязкости жидкости.

Для решения рассматриваемой задачи применяем интегральное преобразование Лапласа

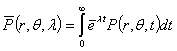(6)

Которое сводит задачи интегрирований (1) при условиях (2)-(5) к интегрированию следующих уравнений, учитывающих начальное условие (5).

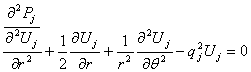(7)

где .

Решение рассматриваемой задачи будем искать в следующим виде

,

(8)

,

.

Неизвестные коэффициенты в (8) можно определить из граничных условий (2)-(5), предварительно применим к ним преобразования Лапласа. Для этого, используя формулу

(9)

где

Если , а если , то в (9) можно меняться местами и .

Сопоставлением коэффициентов при соответствующих тригонометрических функциях, найдем:

,

,

,

,

,

,

,

,

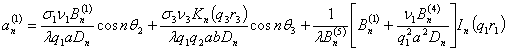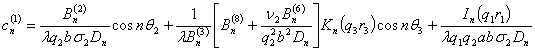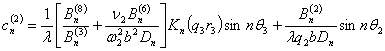где ,

,

,

,

,

,

,

,

Учитывая найденные значения коэффициентов в (8), после некоторых преобразований будем иметь

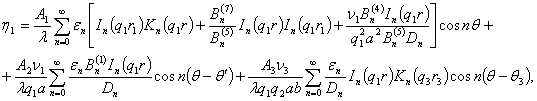
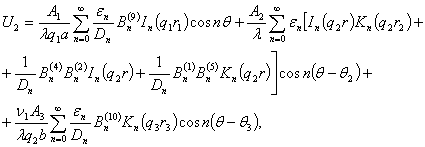(10)

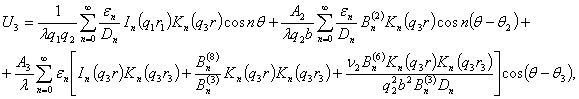
где .

Для больших значений временны, которые соответствуют малым значениям параметром преобразования Лапласа, т.е. и цилиндрические функции, входящие в (10), заменяя первыми членами их разложения в ряд при малых значениях аргумента (кроме функций с нулевыми индексами), получим:

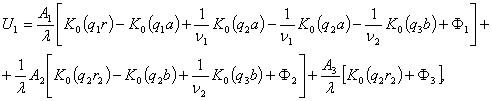
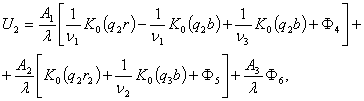(11)

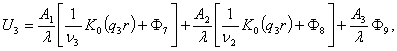
где ,

,

,

,

,

,

,

,

.

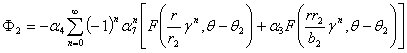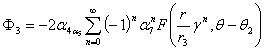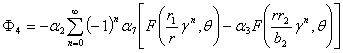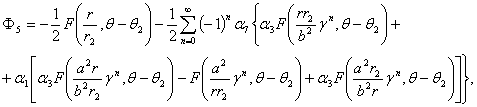
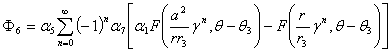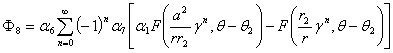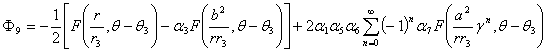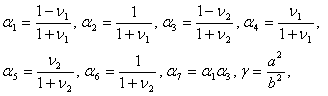
Переходя к оригиналом в (II), будем иметь

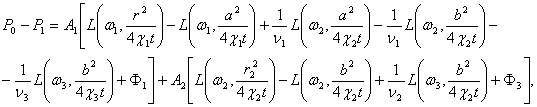
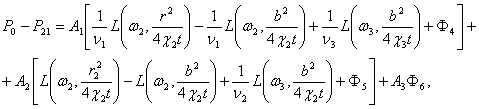(12)

,

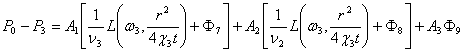где 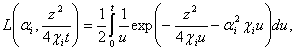при ,

где при больших значений времени с высокой точностью имеет место следующее соотношение

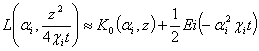
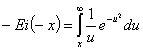– интегральная показательная функция, табулирования.

Полученные формулы удобны для проведения гидродинамических расчетов.

Литература

1. Чугунов В.Д. К определению давления в неоднородных пластах. Изв. Казанского филиала АН СССР, сер. физ.-мат. и тех. наук, №3, 1959.

2. Гусейнов Г.П., Велиев М.Н. Движение упругой жидкости в упругом кусочно- однородном пласте. Труды АН НИИ, вып. 18, 1987.

3. Велиев М.Н., Джаббаров И.И. Движение несжимаемой жидкости в кусочно-однородном пласте со слабопроницаемой кровлей. Изв. АН Аз.ССР, сер. физ.-тех. наук, №3, 1974.

4. Лаврентьев М.А., Шабат В.В. Методы теория функции комплексного переменного. М., Изд-во Физ.мат, 1958.