д.т.н.Джаббаров И.И., Алиева Х.Г., д.т.н.Сафарли И.С., Рзаев М.Т.

Сумгаитский Государственный Университет, Азербайджан

ВЗАИМОДЕЙСТВИЕ В ДВУХ УПРУГИХ СЛАБОПРОНИЦАЕМЫХ ПЕРЕМЫЧКОЙ ПЛАСТАХ

В статье рассмотрены вопросы движения жидкости в двух упругих пласта: кровля и слабопроницаемой подошвы

Ключевые слова. Перемычка, кровля, подошва, проницаемость, пьезопроводность.

В настоящей статье рассматривается движение жидкости в двух упругих пластах, кровля и подошвы слабопроницаемы. Пласты считаются достаточно большими по построению, и каждый состоит из двух зон. Для каждой зоны пласта имеются коэффициенты проницаемости и пьезопроводности соответственно и . Рассматривается случай, когда в каждой пластине имеются две зоны, при переходе через зоны. при которых проницаемость и пьезопроводность изменяется скачком (рис. 1).

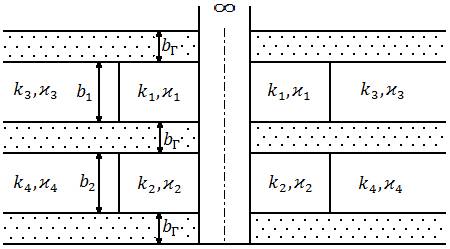
Рис. 1

В начальный момент времени давление во всем пласте считается постоянным и равным , и скважины, работающие с заданными дебитами – и расположены в первых зонах пласта. Требуется определить давление в любой момент времени в произвольной точке пласта.

Математически рассматриваемая задача формируется следующим образом: найти решение следующей системы дифференциальных уравнений в частных производных, в которой учтены слабопроницаемость кровли и подошвы пласта.

(1)

При следующих начальных и граничных условиях

при (2)

при (3)

при (4)

при (5)

(6)

где , , ,

цилиндрические координаты; – усредненные значения функций давления по мощности пласта; – дебиты скважины; – время, – мощность пласта; – коэффициенты проницаемости пласта; – коэффициенты проницаемости перемычки пласта; – коэффициенты пьезопроводности пласта.

Для решении рассматриваемой задачи воспользуемся интегральным преобразованием Лапласа

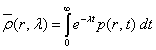
(7)

где параметр преобразования.

Так же как в работе решения задачи для перепадов давления в изображении преобразования Лапласа ищем в виде:

(8)

где ,

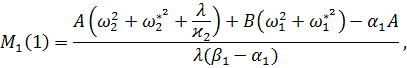
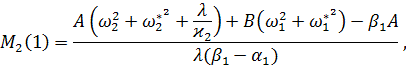
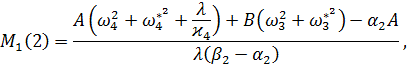
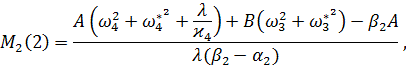
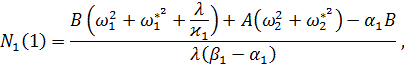
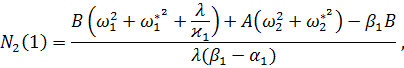
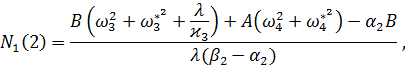
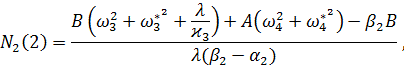
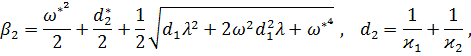
(9)

где .

Отметим, что найденные коэффициенты в (7) оригиналы функций изображений является очень громоздкими и проведение по ним расчетов почти невозможно, поэтому здесь их не будем приводить.

Наиболее практическое и теоретические значение представляет формулы, получение для больших и малых значений времени.

Для малых значений можно принять

(10)

Теперь используя выполнения (10) в изображений давления в зоне (8), где расположена скважина (в зоне с параметрами и , ).

(11)

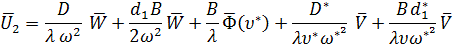
где

Оригинал функций- изображений (11) будем иметь вид:

(12)

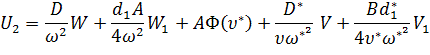
где

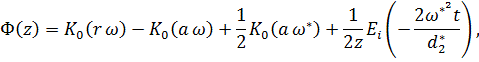
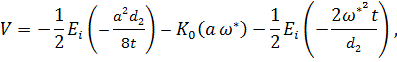
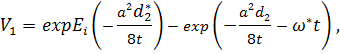
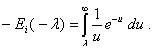
Для больших значений , которые соответствуют малым значениям времени в оригинале

(13)

Если учесть (13) в (8), получаем

(14)

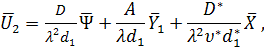
где

,

.

Оригиналы функций- изображений (14) будут иметь вид:

(15)

где

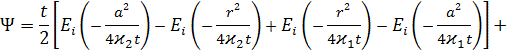
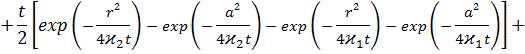
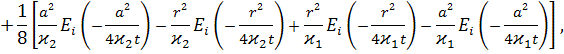
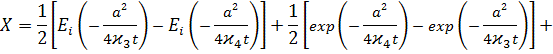
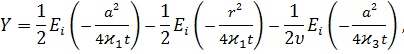
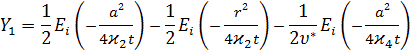
Если процесс не зависит от времени, т.е. процесс является стационарным, для функции давления получим:

(16)

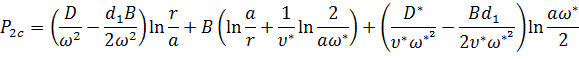
Полученные формулы удобны при гидродинамических расчетах.

Литература

1. Гусейнзаде М. А., Колосовская А. К.– Упругий режим в однопластовых и многопластовых системах. Изд. – “недр”, М., 1972.

2. Джаббаров И., И., Алиева Х. Г. – Неустановившееся движение жидкостей в двух пластах имеющиеся слабопроницаемую перемычку SDU Elmi xəbərlər, cild 2, 2002, №3.

3. Лаврентьев М.,А., Шабат В. В. – Методы теории функции комплексного переменного. Изв-во, Физ.- мат., 1958