К.т.н. Шаров В.В., аспирант Антонов К.А.

Казанский государственный энергетический университет, Россия

Системы контроля сопротивления изоляции роторных электрических машин в условиях эксплуатации.

Проект направлен на совершенствование методов контроля технического состояния основных функциональных параметров электрических машин связанных с надежностью в процессе эксплуатации. В настоящее время контроль сопротивления изоляции электрических машин роторных типов осуществляется, как правило, путем вывода их из работы, для того что бы осуществить контроль сопротивления изоляции. В условиях эксплуатации имеется возможность определять ее величину через температуру статорных обмоток на основе соответствующих уравнений взаимосвязи. Исходя из этого методика определения величины сопротивления изоляции в условиях эксплуатации является актуальны.

Данный проект предлагается для контроля сопротивления изоляции электрооборудования без вывода его из эксплуатации. Схема экспериментальной установки представлена на рис.1

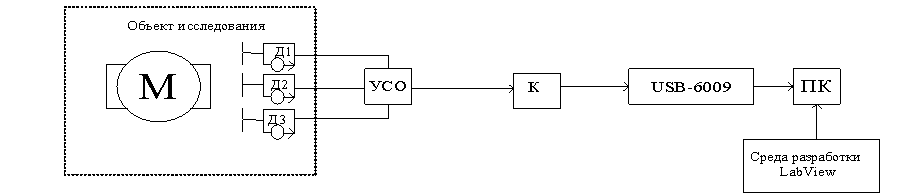
Рис. 1. Схема экспериментальной установки

Практика показывает, что основными факторами, влияющими на срок службы изоляции электрических машин (ЭМ), являются: температура, влага, воздействие электрического поля, механические усилия, агрессивные среды, запыленность и т.п. Из перечисленных факторов во многих случаях доминирует температура и, как следствие, тепловое старение изоляции.

Обмотки ЭМ являются одним из наиболее важных элементов их конструкции, поскольку повреждения изоляции обмоток обычно приводят к тяжелым последствиям и длительным простоям ЭМ в ремонте. Известно, что основным показателем работоспособности ЭМ, является активное сопротивление изоляции обмоток и при его снижении ниже определенного уровня приводит к возрастанию токов утечки и в конечном итоге к пробою изоляции. При изменении температуры изоляции в сторону повышения ускоряются реакции, вызывающие ее старение. Принято считать, что зависимость срока службы изоляции L от температуры θ, °С[1].

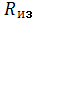Следует иметь в виду, что при изменении температуры изменяется и величина сопротивления изоляции: она уменьшается в 2 раза при повышении температуры на каждые Δθ °С. Таким образом, зная величину сопротивления изоляции при температуре , можно определить величину сопротивления изоляции при температуре θ по формуле:

. (1)

Стандарты на электрические машины оценивают тепловое состояние машины не по температуре ее частей, а по превышению их температуры над температурой охлаждающей среды, которая для нормальных условий эксплуатации принята равной 40°С.

Исходя из полного тока через диэлектрик, имеющего потери релаксационные и сквозной проводимости, получим

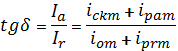. (2)

где все токи имеют амплитудные значения: - ток сквозной проводимости, - безынерционный ток смещения, и - активная и реактивная составляющие релаксационного тока поляризации.

Подставив в уравнение значения токов, выраженных через параметры изоляции, получим

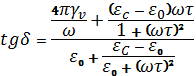. (3)

где - удельная объемная электропроводность диэлектрика; , – статическая (при постоянном токе) и динамическая (при высоких частотах) диэлектрические проницаемости диэлектрика; - постоянная времени релаксации диэлектрика.

При очень низких частотах основными являются потери энергии сквозной проводимости, и

. (4)

На постоянном токе , tgδ →0, и потери сквозной проводимости равны

, (5)

где S - площадь проводящей части обмотки; d - толщина изоляции.

Для диэлектриков с релаксационной поляризацией и малой величиной на высоких частотах основную роль играют релаксационные потери, поэтому слагаемым, содержащим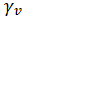 можно пренебречь, и тогда имеем

. (6)

С повышением частоты, т.е. с увеличением ωτ, tgδ вначале растет при малых значениях ωτ, а затем убывает, проходя через максимум. Таким образом, зависимость имеет две составляющие для диэлектриков с релаксационной поляризацией: а) потери на сквозную проводимость (кривая 1, рис. 2, а), которые убывают с ростом ωτ, б) дипольно-релаксационные потери (кривая 2, рис. 2, а), которые имеют максимум. Суммарная зависимость для показана на рис. 2, а (кривая 3) при фиксированной температуре. Время релаксации поляризации r уменьшается с ростом температуры по экспоненциальной зависимости

, (7)

где - постоянная времени; К - постоянная Больцмана; Т - температура;

- энергия активации релаксационных процессов.

При фиксированной температуре время релаксации поляризации диполей остается постоянным , следовательно, и частота тепловых колебаний диполей остается постоянной. Рассмотрим физический смысл дипольно-релаксационных потерь. При низких частотах электрического поля диполи имеют значительно выше частоту тепловых колебаний и поэтому никак не реагируют на низкие частоты поля. По мере увеличения частоты поля ω они начинают ориентироваться по полю. Но частоты поля и диполей существенно различаются, поэтому tgδ постепенно растет с увеличением ω. При частоте поля частота колебаний диполей совпадает с частотой поля, наступает резонанс частот, диполи полностью ориентируются по направлению поля, затрачивая максимум энергии, т.е. наступает максимум кривой 2 (рис. 2).

При дальнейшем увеличении частоты поля наступает дисбаланс частот: частота колебаний диполей при данной температуре остается постоянной, а частота поля увеличивается, поэтому диполи не успевают ориентироваться по полю и затрачивают меньше энергии, tgδ падает. При очень высоких значениях ω диполи не реагируют на изменение электрического поля и поэтому нет затрат энергии, tgδ→0.

С изменением температуры T изменится величина времени релаксации поляризации τ. С увеличением температуры τ уменьшится, при этом увеличится частота тепловых колебаний диполей. Теперь при температуре ; резонанс частот и максимум потерь энергии tgδ наступят при более высокой частоте электрического поля о, т.е. произойдет смещение максимума tgδ в область более высоких частот (вправо). Это наглядно показано на рис. 2, б. Чем больше отличается температура , тем значительнее будет сдвиг максимума вправо. При понижении температуры, т.е. максимум резонансных потерь энергии будет смещаться влево. Это произойдет потому, что с понижением температуры время релаксации поляризации τ увеличится, а частота тепловых колебаний диполей уменьшится, поэтому резонанс частот (колебаний диполей и внешнего электрического поля) наступит при более низкой частоте , так как .

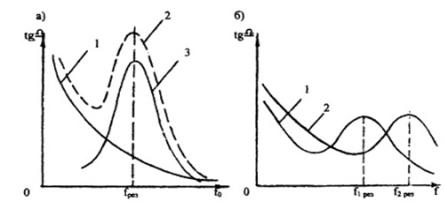
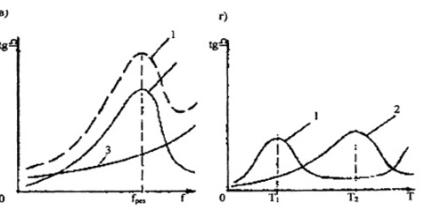
Рис.2. Зависимость от температуры при фиксированной частоте для диэлектриков с релаксационной поляризацией

Зависимость от температуры при фиксированной частоте для диэлектриков с релаксационной поляризацией показана на рис. 2, в:

кривая 1 - от потерь энергии на сквозную проводимость; по мере увеличения температуры растет, так как увеличивается ток сквозной проводимости за счет снижения сопротивления диэлектриков;

кривая 2 - от потерь энергии на релаксационные потери энергии. В этом случае также наступает максимум по тем же причинам, которые были рассмотрены выше;

кривая 3 - суммарная зависимость от температуры с учетом потерь энергии на сквозную проводимость и релаксационные потери.

Для случая зависимости от температуры для двух фиксированных частот также наблюдается смещение максимума в область более высоких температур (см. рис. 2, г), если частота электрического поля ω фиксирована, то изменение температуры приводит к изменению времени релаксации поляризации и, соответственно, частоты колебаний диполей. При достижении частоты колебаний диполей величины частоты электрического поля наступает резонанс частот и наблюдается максимум потерь энергии.

Температурно-частотные зависимости отражают физико-химические свойства диэлектрика, его структуру. Внешние воздействия на диэлектрик эксплуатационных факторов (температуры, влажности, механических напряжений, электрического поля) вызывает структурные изменения диэлектрика, что должно отразиться на зависимостях [2].

Литература:

1. Кузнецов Н.Л. Надежность электрических машин. – М.: Издательский дом МЭИ, 2006. – 432с.

2. Ваксер Н.М. Оценка состояния изоляции генераторов. – СПб.: Издательство СПбГТУ, 2001. – 84с.