К.ф.-м.н. Ележанова Ш.К.
Атырауский государственный университет
им. Х.Досмухамедова, Казахстан
ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ
РАСЩЕПЛЕНИЯ ПРИ РЕШЕНИИ ЗАДАЧ
ПЕРЕНОСА И ДИФФУЗИИ ВЕЩЕСТВА
Развитие
вычислительных машин и численных методов открыли большие перспективы
использования конечно элементного анализа, использование методов конечных
разностей, методы расщепления и т.д. при исследовании проблем переноса и
диффузии субстанции в атмосфере. Известно, что математические модели таких
задач приводится к неоднородным дифференциальным уравнениям в частных
производных второго порядка, удовлетворяющие однородным граничным условиям. Приведения
сложных задач к более простым возможна в тех случаях, когда исходный
положительно полуопределенный оператор представляется в виде суммы положительно
полуопределенных простейших операторов. Такие методы называется методами
расщепления. Первоначальное развитие методы расщепления нестационарных задач
получили в работах Дугласа, Писсмана, Рэчфорда, а затем были развиты в
исследованиях К. А. Багриновского и С.К. Годунова, Н.Н. Яненко, А.А Самарского, Г.И. Марчука [12, 36, 38] и др. В
настоящем времени методы расщепления стал мощным математическим аппаратом
решения весьма сложных нестационарных задач математической физики. Надо
отметить, что теория методов расщепления особенно полно разработана для случая,
когда исходный оператор представлен в виде суммы двух более простых.
Рассмотрим
эволюционную задачу
![]()
![]() в
в ![]() при
при ![]() (1.1)
(1.1)
где оператор ![]() представим в виде
представим в виде
![]() (1.2)
(1.2)
при условии, что ![]() ,
, ![]() (1.3)
(1.3)
Предположим, что решение задачи (1.1) обладает
необходимой гладкостью. Переходим к рассмотрению методов двухкомпонентного
расщепления, предполагая, что задача (1.1) уже редуцирована к разностному виду
и, следовательно, операторы ![]() ,
, ![]() и
и ![]() являются матрицами.
Пусть
являются матрицами.
Пусть ![]()
![]() . Рассмотрим аппроксимации этих матриц на интервале
. Рассмотрим аппроксимации этих матриц на интервале ![]() в форме
в форме ![]()
![]() предполагая, что
элементы матриц
предполагая, что
элементы матриц ![]() ,
, ![]() имеют достаточную
гладкость. Выпишем разностную систему уравнений, предположенную Н.Н.Яненко и
состоящую из последовательного решения простейших схем Кранка-Николсона:
имеют достаточную
гладкость. Выпишем разностную систему уравнений, предположенную Н.Н.Яненко и
состоящую из последовательного решения простейших схем Кранка-Николсона:
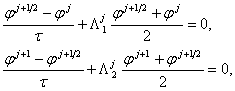 (1.4.)
(1.4.)
Система разностных уравнений (1.4.) после исключения
вспомогательной функции ![]() может быть приведена к одному уравнению
может быть приведена к одному уравнению
![]() (1.5.)
(1.5.)
где ![]() (1.6.)
(1.6.)
Разложим оператор ![]() по степеням
по степеням ![]() , предполагая, что
, предполагая, что ![]() . В результате несложных преобразований получим
. В результате несложных преобразований получим
![]() (1.7.)
(1.7.)
Если операторы ![]() коммутируют, т.е.
коммутируют, т.е. ![]() , разложение (1.7.) можно записать в виде
, разложение (1.7.) можно записать в виде
![]() (1.8.)
(1.8.)
Таким образом, если ![]()
![]() , то при достаточной гладкости элементов матриц и решения
, то при достаточной гладкости элементов матриц и решения ![]() задачи (1.1.)-(1.3.) разностная схема (1.4.)
абсолютно устойчива (это следует из справедливого, согласно лемме Келлога,
неравенства
задачи (1.1.)-(1.3.) разностная схема (1.4.)
абсолютно устойчива (это следует из справедливого, согласно лемме Келлога,
неравенства ![]() ) и аппроксимирует исходное уравнение (1.1.) со вторым
порядком по
) и аппроксимирует исходное уравнение (1.1.) со вторым
порядком по ![]() в случае, если
в случае, если ![]() и
и ![]() коммутативны, и с первым порядком, если они
не коммутативны. Теперь будем аппроксимировать операторы
коммутативны, и с первым порядком, если они
не коммутативны. Теперь будем аппроксимировать операторы ![]() и
и ![]() не на интервале
не на интервале ![]() , как это было в (1.4.), а на интервале
, как это было в (1.4.), а на интервале ![]() , положив
, положив ![]() .
.
Рассмотрим следующие две системы разностных уравнений:
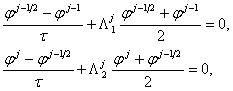 (1.9.)
(1.9.)
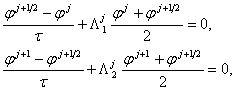 (1.10.)
(1.10.)
Цикл вычислений состоит именно в поочередном
применении разностных схем (1.9.), (1.10.). Аналогично предыдущему, можно
показать, что на полном цикле вычислений с помощью (1.9.) и (1.10.) будем иметь
![]() (1.11.)
(1.11.)
где 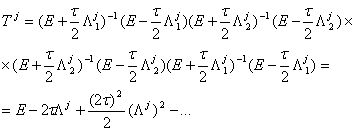 (1.12.)
(1.12.)
Если оператор ![]() сравнить с оператором шага схемы
Кранка-Николсона
сравнить с оператором шага схемы
Кранка-Николсона
![]() (1.13.)
(1.13.)
то можно установить, что с точностью до величины ![]() оператор шага
оператор шага ![]() для двуциклической схемы расщепления
совпадает с оператором шага схемы Кранка-Николсона, примененной к удвоенному
интервалу по времени, независимо от того, коммутативны операторы
для двуциклической схемы расщепления
совпадает с оператором шага схемы Кранка-Николсона, примененной к удвоенному
интервалу по времени, независимо от того, коммутативны операторы ![]() или нет. Таким образом, этот прием
существенно снижает ограничение о коммутативности операторов.
или нет. Таким образом, этот прием
существенно снижает ограничение о коммутативности операторов.
Переходим к обсуждению вопроса о счетной устойчивости
метода. Рассмотрим неоднородную задачу и нахождение ее решения с помощью
двуциклического полного расщепления. С этой целью рассмотрим систему разностных
уравнений вида (1.9.), (1.10.), записанных в более удобной форме:
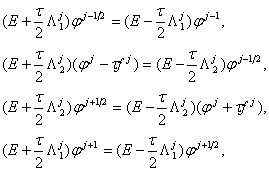 (1.14.)
(1.14.)
где ![]() . Разрешая эти уравнения относительно
. Разрешая эти уравнения относительно ![]() , получим
, получим
![]() (1.15.)
(1.15.)
где
![]() (1.16.)
(1.16.)
![]()
![]() (1.17.)
(1.17.)
С помощью разложения по степеням малого параметра ![]() приведем (1.17.) к виду
приведем (1.17.) к виду ![]() (1.18.)
(1.18.)
затем преобразуем к виду
![]() ,
(1.19.)
,
(1.19.)
и исключим ![]() . Для этого воспользуемся разложением решения в ряд Тейлора в
окрестности точки
. Для этого воспользуемся разложением решения в ряд Тейлора в
окрестности точки ![]() . С точностью до
. С точностью до ![]() имеем
имеем
![]() (1.20.)
(1.20.)
Производную ![]() исключим с помощью равенства
исключим с помощью равенства
![]() (1.21.)
(1.21.)
Подставив (1.21.) в (1.20.), получим ![]() откуда
откуда
![]() (1.22.)
(1.22.)
Подставляя
теперь (1.22.) в (1.21.) находим ![]() (1.23.)
(1.23.)
Очевидно, что уравнение (1.23.) аппроксимирует
исходное уравнение (1.1.) на интервале ![]() со вторым порядком
точности по
со вторым порядком
точности по ![]() . Таким образом, найдена разностная аппроксимация
неоднородного эволюционного уравнения второго порядка с помощью двуциклического
метода.
. Таким образом, найдена разностная аппроксимация
неоднородного эволюционного уравнения второго порядка с помощью двуциклического
метода.
Устойчивость метода доказывается в энергетической
норме элементарно. В самом деле, оценим ![]() из (1.15.) по норме:
из (1.15.) по норме:
![]() (1.24.)
(1.24.)
Учитывая, что ![]() , а значит,
, а значит, ![]() , имеем
, имеем
![]() (1.25.)
(1.25.)
С помощью рекуррентного соотношения (1.15.) получим
![]() (1.26.)
(1.26.)
где ![]() . Из соотношения (1.26.) следует счетная устойчивость схемы
на любом конечном временном интервале. Систему уравнений (1.14.) можно записать
также в следующей эквивалентной форме:
. Из соотношения (1.26.) следует счетная устойчивость схемы
на любом конечном временном интервале. Систему уравнений (1.14.) можно записать
также в следующей эквивалентной форме:
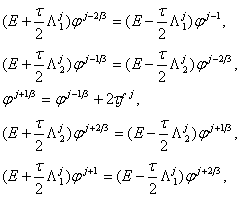 (1.27.)
(1.27.)
Исключив неизвестные с дробными индексами, приходим к
разрешенному уравнению ![]() (1.28.), которое совпадает с (1.15.). В
некоторых случаях запись уравнений в форме (1.27.) более предпочтительна, чем в
форме (1.14.). Итак, если матрицы
(1.28.), которое совпадает с (1.15.). В
некоторых случаях запись уравнений в форме (1.27.) более предпочтительна, чем в
форме (1.14.). Итак, если матрицы ![]() ,
, ![]() , то при достаточной
гладкости решения
, то при достаточной
гладкости решения ![]() , функции
, функции ![]() и элементов матриц
и элементов матриц ![]() ,
, ![]() , система разностных
уравнений (1.14.) абсолютно устойчива на интервале
, система разностных
уравнений (1.14.) абсолютно устойчива на интервале ![]() и аппроксимирует исходное уравнение со вторым
порядком по
и аппроксимирует исходное уравнение со вторым
порядком по ![]() .
.
Литература:
1
Марчук
Г.И. Математическое моделирование в проблеме окружающей среды. –М.: Наука,
1982. –320 с.
2
Пененко
В.В., Алоян А.Е. Модели и методы для охраны окружающей среды. –Н.: Наука, 1985.
–274 с.
3
Ковеня
В.М., Яненко Н.Н. Метод расщепления в задачах газовой динамики. –Новосибирск:
Наука, 1981. –С. 95-99.
4
Марчук
Г.И. Численные методы. –М.: Наука, 1988. –214 с.
5
Мардонов
Б.М., Муликов Р.Р, Кушкенбаев М.У., Ележанова Ш.К. (Мухамбетова Ш.К.) Исследование
процессов распространения и трансформации загрязняющихся веществ в нижнем слое
атмосферы и почвенной среде. Монография. –Атырау: Атырауский институт нефти и
газа, 2005. –160 с.