Математика/4. Прикладная математика
К.ф.-м.н. Зинченко А.Б., Битюцкий М.С.
Южный федеральный университет. Россия
Параметрическое описание некоторых классов ТП-игр
с одноточечным С-ядром
Для кооперативной
игры с трансферабельной полезностью (ТП-игры) ![]() , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() , предложено много концепций решения. Наиболее популярным,
простым и интуитивным решением-множеством является С-ядро
, предложено много концепций решения. Наиболее популярным,
простым и интуитивным решением-множеством является С-ядро ![]() . Если игроков устраивает принцип справедливости, реализуемый
этим решением, то возникает проблема
выбора единственного вектора индивидуальных выигрышей
. Если игроков устраивает принцип справедливости, реализуемый
этим решением, то возникает проблема
выбора единственного вектора индивидуальных выигрышей ![]() (исхода игры).
Задача не тривиальная, т.к.
(исхода игры).
Задача не тривиальная, т.к. ![]() -ядро может быть относительно большим и даже совпадать с множеством
всех дележей. Следовательно, представляет интерес
описание классов игр с одноточечным С-ядром
-ядро может быть относительно большим и даже совпадать с множеством
всех дележей. Следовательно, представляет интерес
описание классов игр с одноточечным С-ядром ![]() и соответствующих
дележей
и соответствующих
дележей ![]() .
.
Инвариантность С-ядра
относительно (0,1)-нормализации позволяет ограничиться рассмотрением класса
(0,1)-нормализованных сбалансированных игр с ![]() участниками
участниками ![]() . Обозначим через
. Обозначим через ![]() подмножество игр,
удовлетворяющих условиям
подмножество игр,
удовлетворяющих условиям ![]() ,
,![]() . Знание экстремальных игр (вершин многогранника
. Знание экстремальных игр (вершин многогранника ![]() ) полезно для описания поведения других, отличных от С-ядра,
решений. Было замечено, что геометрическая экстремальность часто соответствует
экстремальному социальному поведению некоторых агентов.
) полезно для описания поведения других, отличных от С-ядра,
решений. Было замечено, что геометрическая экстремальность часто соответствует
экстремальному социальному поведению некоторых агентов.
В
доказательствах утверждений используется
проекция
![]() (1)
(1)
множества ![]() на
на ![]() . Если
. Если ![]() , то соответствующее
, то соответствующее ![]() определяется (1).
Обратно, каждому
определяется (1).
Обратно, каждому ![]() соответствует игра
соответствует игра ![]() , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для параметрического
описания ![]() будем использовать условие
Бондаревой-Шепли [1]-[2]. Пусть
будем использовать условие
Бондаревой-Шепли [1]-[2]. Пусть ![]() . Рассмотрим
множество экстремальных точек
. Рассмотрим
множество экстремальных точек ![]() многогранника
многогранника ![]() , заданного системой
, заданного системой ![]() .
Набор
.
Набор ![]() коалиций
коалиций ![]() является минимальным сбалансированным множеством
(м.с.м.), если существует такая точка
является минимальным сбалансированным множеством
(м.с.м.), если существует такая точка ![]() , что
, что ![]() для
для ![]() , и
, и ![]() для
для ![]() . Вектор
. Вектор ![]() , где
, где ![]() , называется весом
м.с.м. Семейство всех м.с.м. обозначим через
, называется весом
м.с.м. Семейство всех м.с.м. обозначим через ![]() . Игра
. Игра ![]() сбалансирована, т.е.
сбалансирована, т.е. ![]() , тогда и только тогда, когда она удовлетворяет условию
, тогда и только тогда, когда она удовлетворяет условию
![]() ,
, ![]() . Для (0,1)-нормализованных игр это условие принимает вид
. Для (0,1)-нормализованных игр это условие принимает вид
![]() ,
, ![]() .
(2)
.
(2)
Минимальное сбалансированное множество ![]() , соответствующее невырожденной крайней точке
, соответствующее невырожденной крайней точке ![]() , назовем невырожденным. Обозначим через
, назовем невырожденным. Обозначим через ![]() подмножество невырожденных м.с.м. Для любого
подмножество невырожденных м.с.м. Для любого ![]() справедливо
справедливо ![]() . Сбалансированная игра
. Сбалансированная игра ![]() имеет одноточечное
С-ядро тогда и только тогда, когда, существует м.с.м.
имеет одноточечное
С-ядро тогда и только тогда, когда, существует м.с.м. ![]() , для которого (2) выполняется как равенство [1].
, для которого (2) выполняется как равенство [1].
Известно , что многогранник ![]() имеет 5 вершин, среди
которых не вырождены две вершины, соответствующие м.с.м.
имеет 5 вершин, среди
которых не вырождены две вершины, соответствующие м.с.м. ![]() , и
, и ![]() с весами (1,1,1) и
(1/2,1/2,1/2). Условие сбалансированности произвольной игры трех лиц имеет вид
с весами (1,1,1) и
(1/2,1/2,1/2). Условие сбалансированности произвольной игры трех лиц имеет вид
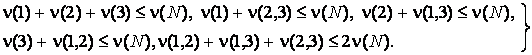 (3)
(3)
Невырожденному
м.с.м. ![]() соответствует первое
неравенство из (3). Заменив его равенством, получаем систему, определяющую
несущественную игру, в которой С-ядро совпадает с одноточечным множеством
дележей
соответствует первое
неравенство из (3). Заменив его равенством, получаем систему, определяющую
несущественную игру, в которой С-ядро совпадает с одноточечным множеством
дележей ![]() . Эта игра не имеет
(0,1)-формы.
. Эта игра не имеет
(0,1)-формы.
Подставив в (3) значения ![]() ,
, ![]() , и
, и ![]() , получаем условие сбалансированности (0,1)-нормализованной
игры 3 лиц
, получаем условие сбалансированности (0,1)-нормализованной
игры 3 лиц
![]() ,
, ![]() .
.
Минимальное сбалансированное множество ![]() соответствует последнему
неравенству системы (3). Заменив его равенством, получаем, что
соответствует последнему
неравенству системы (3). Заменив его равенством, получаем, что ![]() тогда и только тогда,
когда выполняется условие
тогда и только тогда,
когда выполняется условие
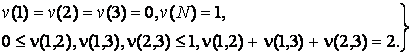
Используя взаимно однозначное соответствие между ![]() и
и
![]() ,
,
достаточно исследовать структуру ![]() . Многогранник
. Многогранник ![]() имеет три вершины (экстремальные точки)
имеет три вершины (экстремальные точки) ![]() ,
, ![]() и
и ![]() , т.е.
, т.е.
![]() .
.
Каждой вершине ![]() соответствует простая
невыпуклая игра
соответствует простая
невыпуклая игра ![]() большого босса с агентом
большого босса с агентом ![]() в качестве босса. Согласно
дележам
в качестве босса. Согласно
дележам ![]() ,
, ![]() и
и ![]() , всю распределяемую сумму
, всю распределяемую сумму ![]() получает босс. Два остальных
агента, не являющиеся нулевыми игроками, получают нулевой выигрыш. Значения
Шепли
получает босс. Два остальных
агента, не являющиеся нулевыми игроками, получают нулевой выигрыш. Значения
Шепли ![]() ,
, ![]() ,
, ![]() являются интуитивно
более справедливыми, однако большая часть
являются интуитивно
более справедливыми, однако большая часть ![]() достается боссу. В
таблицах 1 и 2 приведены некоторые из
достается боссу. В
таблицах 1 и 2 приведены некоторые из ![]() , а также единственные элементы С-ядер и значения Шепли соответствующих
им игр
, а также единственные элементы С-ядер и значения Шепли соответствующих
им игр ![]() .
.
Таблица 1
Игры,
принадлежащие ребру многогранника ![]() (
(![]() )
)
|
(b1, b2) |
|
доминирование игроков |
|
|
|
( |
|
|
|
|
|
( |
|
|
|
|
|
( |
|
|
|
|
|
( |
|
|
|
|
|
( |
|
|
|
|
Утверждение 1. Только экстремальные игры ![]() ,
, ![]() , многогранника
, многогранника ![]() имеют вето-игрока, но для многогранников
имеют вето-игрока, но для многогранников ![]() ,
,![]() , это не верно.
, это не верно.
Доказательство. Игра ![]() имеет вето-игрока
имеет вето-игрока ![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]() ,
,![]() . Положив
. Положив ![]() и подставив в (3)
значение n(2,3) =0, получаем систему
и подставив в (3)
значение n(2,3) =0, получаем систему
![]() ,
, ![]() ,
,
имеющую единственное решение ![]() , соответствующее
, соответствующее ![]() . Аналогично, для
. Аналогично, для ![]() и
и ![]() получаем единственные игры
получаем единственные игры
![]() , соответствующие
, соответствующие ![]() . Рассмотрим игру
. Рассмотрим игру ![]() лиц, в которой
лиц, в которой ![]() ,
, ![]() ,
, ![]() ,
, ![]() для
для ![]() ,
, ![]() в остальных
случаях. С-ядро этой игры – одноточечное
в остальных
случаях. С-ядро этой игры – одноточечное
![]() , значит,
, значит, ![]() . Агент 1 является вето-игроком, но
. Агент 1 является вето-игроком, но ![]() , т.к.
, т.к. ![]() , где
, где ![]() ,
, ![]() для
для ![]() ,
, ![]() в остальных случаях.
Очевидно, что
в остальных случаях.
Очевидно, что ![]() . •
. •
Утверждение 2. Все игры из ![]() не имеют нулевых
игроков.
не имеют нулевых
игроков.
Доказательство.
Игрок ![]() является нулевым в
является нулевым в ![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]() ,
, ![]() . Если
. Если ![]() , то, учитывая
, то, учитывая ![]() получаем
получаем ![]() . Из уравнения
. Из уравнения ![]() следует, что
следует, что ![]() . Но это противоречит
условию
. Но это противоречит
условию ![]() . Аналогично для
. Аналогично для ![]() . •
. •
Утверждение 3. Если игра ![]() принадлежит ребру
многогранника
принадлежит ребру
многогранника ![]() , т.е.
, т.е. ![]() для некоторого
для некоторого![]() , то при дележе
, то при дележе ![]() выигрыш, по крайней мере, одного ненулевого
игрока равен нулю.
выигрыш, по крайней мере, одного ненулевого
игрока равен нулю.
Доказательство.
Согласно утверждению
2, любая игра ![]() не имеет ненулевых
игроков. Без ограничения общности, положим,
не имеет ненулевых
игроков. Без ограничения общности, положим,
![]() и рассмотрим
и рассмотрим
![]() ,
,
где
![]() ,
, ![]() . Подставив игру
. Подставив игру
![]() , соответствующую
, соответствующую ![]() , в систему,
определяющую С-ядро
(0,1)-нормализованной игры 3 лиц, получаем систему
, в систему,
определяющую С-ядро
(0,1)-нормализованной игры 3 лиц, получаем систему
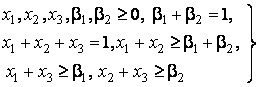 ®
® 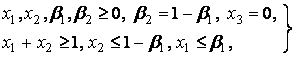
разрешимость
которой вытекает из сбалансированности игры ![]() . Следовательно,
. Следовательно, ![]() , где
, где ![]() удовлетворяют предыдущей системе. •
удовлетворяют предыдущей системе. •
Утверждение 4. Многогранник ![]() не пересекается с
многогранником выпуклых игр трех лиц. Однако существуют игры
не пересекается с
многогранником выпуклых игр трех лиц. Однако существуют игры![]() , в которых значение Шепли совпадает с единственным элементом
, в которых значение Шепли совпадает с единственным элементом
![]() С-ядра.
С-ядра.
Доказательство. Игра ![]() выпукла тогда и только
тогда, когда
выпукла тогда и только
тогда, когда
![]() ,
, ![]() .
.
Для (0,1)-нормализованной игры трех лиц условие выпуклости имеет вид
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Складывая три последних неравенства, получаем ![]() , что противоречит уравнению
, что противоречит уравнению ![]() . Для доказательства второй части утверждения достаточно
рассмотреть симметричную игру
. Для доказательства второй части утверждения достаточно
рассмотреть симметричную игру ![]() , соответствующую вектору
, соответствующую вектору ![]() (см.таблицу 2). •
(см.таблицу 2). •
Таблица 2
Внутренние
элементы многогранника ![]()
|
(b1, b2, b3) |
|
доминирование игроков |
|
|
|
( |
|
|
|
|
|
( |
|
|
|
|
|
( |
|
|
|
|
|
( |
|
|
|
|
Перенумеруем элементы семейства ![]() в произвольном порядке
в произвольном порядке
![]() . Предположим, что первое неравенство системы (3) соответствует
м.с.м.
. Предположим, что первое неравенство системы (3) соответствует
м.с.м. ![]() , второе неравенство - м.с.м.
, второе неравенство - м.с.м. ![]() и т.д. Обозначим через
и т.д. Обозначим через
![]() многогранник,
определенный системой, полученной из (2) заменой
многогранник,
определенный системой, полученной из (2) заменой ![]() -го неравенства
уравнением. В следующей теореме описана структура
-го неравенства
уравнением. В следующей теореме описана структура ![]() для
для ![]() .
.
Утверждение 4. Пусть ![]() . Тогда:
. Тогда:
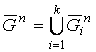 , где
, где ![]() ; множество
; множество ![]() не выпуклое
не выпуклое
Доказательство. a) Если ![]() , то
, то ![]() и при увеличении
и при увеличении ![]() значение
значение ![]() возрастает. Возьмем
возрастает. Возьмем ![]() . Тогда существует такое м.с.м.
. Тогда существует такое м.с.м. ![]() , что
, что ![]() удовлетворяет
удовлетворяет ![]() -му неравенству из (2) как равенству, т.е.
-му неравенству из (2) как равенству, т.е. ![]() . Значит,
. Значит, 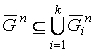 . Обратно, пусть
. Обратно, пусть ![]() для некоторого
для некоторого ![]() . Тогда
. Тогда ![]() удовлетворяет как
равенству, по крайней мере, одному неравенству системы (2), соответствующему
м.с.м. из
удовлетворяет как
равенству, по крайней мере, одному неравенству системы (2), соответствующему
м.с.м. из ![]() . Согласно [1],
игра
. Согласно [1],
игра ![]() имеет одноточечное
С-ядро. Значит,
имеет одноточечное
С-ядро. Значит, ![]() . Следовательно,
. Следовательно, 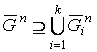 . Рассмотрим две
простых игры
. Рассмотрим две
простых игры ![]() и
и ![]() , определенные множествами выигрывающих коалиций
, определенные множествами выигрывающих коалиций ![]() и
и ![]() . Из
. Из ![]() и
и ![]() вытекает, что
вытекает, что ![]() . Возьмем
. Возьмем ![]() . Тогда
. Тогда ![]() ,
, ![]() ,
, ![]() ,
, ![]() для остальных
для остальных ![]() . Из
. Из ![]() следует, что
следует, что ![]() . •
. •
Утверждение 5. В классе ![]() С-ядро удовлетворяет
аксиоме симметричности.
С-ядро удовлетворяет
аксиоме симметричности.
Доказательство. Известно, что С-ядро
сбалансированной игры ![]() содержит симметричное
ядро [3], которое удовлетворяет аксиоме симметричности. Из предположения об
одноточечности С-ядра следует его совпадение с симметричным ядром для всех игр
из
содержит симметричное
ядро [3], которое удовлетворяет аксиоме симметричности. Из предположения об
одноточечности С-ядра следует его совпадение с симметричным ядром для всех игр
из ![]() . š
. š
Литература:
1. Бондарева О.Н. Некоторые применения методов
линейного программирования к теории кооперативных игр // Проблемы кибернетики.
1963. Вып. 10. С. 119-140.
2.
Shapley L. S.
On balanced sets and cores // Naval Research Logistics Quarterly. 1967. Vol.
14. P. 453-460.
3. Зинченко А.Б. Полусимметричные
ТП-игры // Известия высших учебных заведений.
Северо-Кавказский регион. Естественные науки.. 2012. № 5. С. 10-14.