Дубовик С.В.

Українська академія банківської справи Національного банку України

Маркетингова оцінка попиту на інвестиційні банківські послуги в розрізі їх порівняльної ефективності

Інвестиційні послуги банків, як об`єкт внутрішніх та/або зовнішніх маркетингових досліджень, на нашу думку, повинні аналізуватись в розрізі порівняльної ефективності по відношенню до альтернатив, які пропонуються банками на фінансовому ринку. До таких альтернатив, у першу чергу, належить вже існуючий («класичний») набір послуг, які пов`язані з проведенням банками кредитних та багатьох інших видів операцій, що мають за мету обслуговування проектів фінансового забезпечення підприємств.

В даному контексті поведінка корпоративних клієнтів – споживачів ІБП (в якості об`єкта дослідження оберемо послуги з організації IPO/SPO, або послуги андеррайтингу) та «класичних» банківських послуг (у нашому випадку – кредитне проектне фінансування) може бути з певним значенням ймовірності графічно описана за допомогою двомірного простору споживчих благ, вартість яких позначимо за та відповідно (рис. 1). В межах даного простору реалізується цільова функція споживання клієнта: , де K – спеціальний параметр, що характеризує рівень цільової функції. В нашому випадку параметр K відображає кількісні обмеження за конкретними інвестиційними проектами компанії-клієнта та відображається на площині у вигляді набору кривих байдужості (), які відповідають різним значенням K ().

В Україні серед переліку інвестиційних послуг саме андеррайтинг почав якісно та кількісно розвиватись і набув значної популярності серед корпоративних банківських клієнтів. Слід однак наголосити, що операції з андеррайтингу можуть проводити лише найбільші фінустанови та їх синдикати, оскільки обсяги випуску цінних паперів у більшості випадків становлять від сотень мільйонів до кількох мільярдів гривень [2].

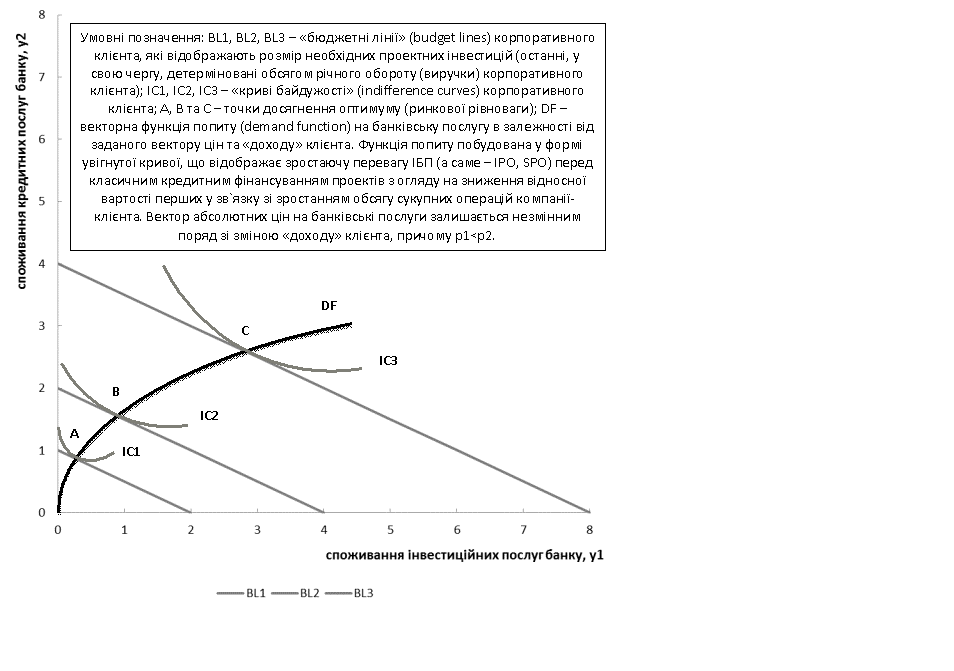
Рисунок 1 – Векторна функція попиту корпоративних клієнтів на банківські послуги (авторська розробка)

Найголовніші властивості цільової функції споживання банківського корпоративного клієнта можна звести до наступного переліку [3]:

1. Функція за своєю природою є зростаючою залежністю від усієї сукупності формуючих її аргументів, тобто зростання обсягу споживання будь-якого блага (банківської послуги) за незмінного рівня споживання всіх інших благ збільшує рівень даної функції. Тому крива байдужості, більш віддалена від початку координат, відповідає вищому значенню цільової функції споживання банківської послуги, а сам процес максимізації в межах виокремленої множини допустимих векторів слід інтерпретувати як алгоритм знаходження точки оптимуму, що знаходиться на максимальній відстані від початку координат площини.

2. Криві байдужості споживача банківської послуги не можуть перетинатися, тобто через певну точку простору «кредитні послуги – інвестиційні послуги» можна провести лише одну криву, яка відображає постійний рівень задоволення клієнта від споживання двох альтернатив. В протилежному випадку один і той же набір банківських послуг мав би одночасно відповідати різним рівням інвестиційних потреб компанії-клієнта, а відповідно і розміру її виручки протягом звітного періоду.

3. Криві байдужості споживача є випуклими, тобто мають від`ємний нахил до кожної осі координат, який поступово скорочується під час руху в додатному напрямку до кожної осі.

При побудові моделі поведінки споживачів на ринку банківських продуктів слід виходити з припущення щодо прагнення даних суб`єктів максимізувати ступінь задоволення власних потреб під час здійснення вибору між двома різними продуктами. Відповідно до цього, проста модель споживчої поведінки матиме наступний векторний вигляд:

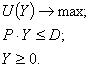(1)

де – попит з боку споживачів на конкретний банківський продукт, – ціна банківської послуги (продукту), D – обсяг проектного фінансування («дохід» компанії-споживача), що задовольняє бюджетному обмеженню: .

Для задачі нелінійного програмування можна застосувати функцію Лагранжа, котра для моделі двох банківських послуг (1) має вигляд [4]:

, (2)

де спеціальний множник Лагранжа () є оптимальною оцінкою «доходу» компанії-клієнта банку.

Множники Лагранжа, відповідаючи оптимальному рішенню споживача банківських послуг, є аналогією подвійних оцінок обмежень задачі лінійного програмування. Останні відображають величину зміни вільного члена обмеження, котрому відповідає множник Лагранжа, в дуже малій площині навколо точки оптимуму. Виходячи з положень теореми Куна-Таккера [1, 5], якщо зазначене обмеження можна розглядати в якості балансу банківської послуги (з одночасною максимізацією вигоди від її придбання), то множник Лагранжа у точці оптимуму відповідає оптимальній ціні послуги:

1. якщо знайдеться ринок, на якому послуга має меншу вартість, то її придбання збільшує економічну вигоду агента;

2. якщо знайдеться ринок, на якому послуга має більшу вартість, то відмова від її придбання збільшує економічну вигоду агента.

Знаходження часткової похідної функції через можна інтерпретувати як визначення граничної корисності банківської послуги, оскільки вона характеризує приріст цільової функції споживання при збільшенні користування даною послугою на окрему «малу одиницю».

Математичний вираз для знаходження оптимального рішення банківського клієнта з використанням теореми Куна-Таккера матиме наступний вигляд [4]:

; ; (3)

При цьому мають місце наступні вирази:

1. , якщо банківська послуга придбавається,

2. , якщо банківська послуга не придбавається,

3. .

Нерівність (3) демонструє ситуацію повного фінансування компанією інвестиційного проекту, що відображає здатність банківського клієнту адекватно оцінити можливості розширення власного бізнесу. Відповідно, справедливою є нерівність .

Із умов досягнення оптимуму (3) випливає наступне співвідношення:

, якщо . (4)

Така умова означає, що клієнт банку має підбирати для себе відповідну послугу таким чином, щоб співвідношення граничної корисності до вартості послуги залишалося однаковим для всіх послуг, які придбаваються клієнтом. Іншими словами, оптимальний набір передбачає пропорційність граничної корисності кожної з обраних послуг (у тому числі інвестиційної) їх вартості.

Література:

1. Исследование операций в экономике: Учебн. пособие для вузов / Под ред. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.

2. Метлушко О. Застосування андеррайтингу у банківській практиці / О. Метлушко // Світ фінансів. – № 3(20). – 2009. – С. 160-165.

3. Нуреев Р.М. Курс микроэкономики: Учебник для вузов / Р.М. Нуреев. – 2-е изд., изм. – М.: Норма, 2004. – 576 с.

4. Федосеев В.В. Экономико-математические методы и модели в маркетинге: Учеб. пособие для вузов / В.В. Федосеев, Н.Д. Эриашвили / Под ред. В.В. Федосеева. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА. – 2001. – 159 с.

5. Шелобаев С.И. Экономико-математические методы и модели: Учеб. пособие для вузов / С.И. Шелобаев – М.: ЮНИТИ-ДАНА, 2005.