Математика / 3. Теория вероятностей и математическая статистика

к.ф.-м. н. Калжанов М.У.

Костанайский государственный университет

имени А.Байтурсынова

Моделирование процесса размножения и гибели

Процессы размножения и гибели являются частным случаем марковских случайных процессов, которые тем не менее находят весьма широкое применение при исследовании дискретных систем со стохастическим характером функционирования.

В случае процесса размножения и гибели с дискретным временем вероятности переходов между состояниями

Здесь d_i - вероятность того, что на следующем шаге (в терминах биологической популяции) произойдет одна гибель, уменьшающая объем популяции до i-1 при условии, что на данном шаге объем популяции равен i. Аналогично, b_i - вероятность рождения на следующем шаге, приводящего к увеличению объема популяции до i+1; 1-d_i-b_i представляет собой вероятность того, что ни одно из этих событий не произойдет и на следующем шаге объем популяции не изменится

Матрица вероятностей переходов для общего процесса размножения и гибели имеет следующий вид:

Т=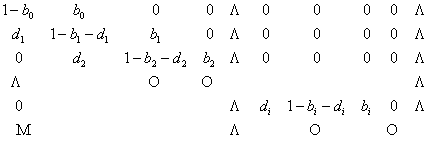

Далее будем рассматривать только непрерывные процессы размножения и гибели, в которых переходы из состояния E_i возможны только в соседние состояния E_i-1 (гибель) и E_i+1 (рождение). Обозначим через l_i интенсивность размножения; она описывает скорость, с которой происходит размножение в популяции объема i. Аналогично, через m_i обозначим интенсивность гибели, задающую скорость с которой происходит гибель в популяции объема i. Заметим, что введенные интенсивности размножения и гибели не зависят от времени, а зависят только от состояния E_i, следовательно, получаем непрерывную однородную цепь Маркова типа размножения и гибели. Эти специальные обозначения введены потому, что они непосредственно приводят к обозначениям, принятым в теории дискретных систем. В зависимости от ранее введенных обозначений имеем:

l_i= q_i,i+1 и m_i= q_i,i-1.

Требование о допустимости переходов только в ближайшие соседние состояния означает, что q_ii=-(m_i+ l_i). Таким образом, матрица интенсивностей переходов общего однородного процесса размножения и гибели принимает вид

.

Q =

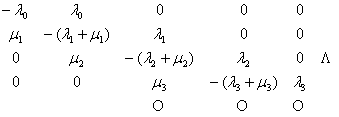
Более точное определение непрерывного процесса размножения и гибели состоит в следующем: некоторый процесс представляет собой процесс размножения и гибели, если он является однородной цепью Маркова с множеством состояний {E₀, E₁, E₂, …}, если рождение и гибель являются независимыми событиями (это вытекает непосредственно из марковского свойства) и если выполняют следующие условия:

1) Pr [точно 1 рождение в промежутке времени (t,t+Δt)| объем популяции равен i]= ;

2) Pr [точно 1 гибель в промежутке времени (t,t+Δt)| объем популяции равен i]= ;

3) Pr [точно 0 рождений в промежутке времени (t,t+Δt)| объем популяции равен i]= ;

4) Pr [точно 0 гибелей в промежутке времени (t,t+Δt)| объем популяции равен i]= .

Вероятность того, что непрерывный процесс размножения и гибели в момент времени t находится в состоянии E_i (объем популяции равен i) в виде

(1)

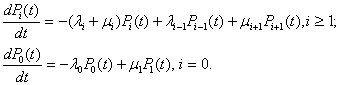
Для решения полученной системы дифференциальных уравнений в нестационарном случае, когда вероятности P_i(t), i=0,1,2,…, зависят от времени, необходимо задать распределение начальных вероятностей P_i(0), i=0,1,2,…, при t=0. Кроме того, должно удовлетворяться нормировочное условие.

Рассмотрим теперь простейший процесс чистого размножения, который определяется как процесс, для которого m_i = 0 при всех i. Кроме того, для еще большего упрощения задачи предположим, что l_i=l для всех i=0,1,2,... . Подставляя эти значения в уравнения (1) получим

(2)

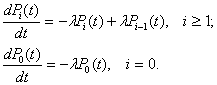
Предположим также, что процесс начинается в нулевой момент при нуле членов, то есть:

(3)

Отсюда для P₀(t) получаем решение

P₀(t)=e^-lt.

Подставляя это решение в уравнение (19) при i = 1, приходим к уравнению

.

Решение этого дифференциального уравнения, очевидно, имеет вид

P₁(t)= lte^-lt.

Далее по индукции в качестве решения уравнения (3) находим

.

Это знакомое распределение Пуассона.

Таким образом, процесс чистого размножения с постоянной интенсивностью l приводит к последовательности рождений, образующей пуассоновский процесс.

Литература:

1. Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1971 г.

2. Вентцель Е.С. Теория вероятностей. М.: Наука, 1964 г.