МОДЕЛИРОВАНИЕ КОМПОЗИТОВ
Хнаев О.А., Данилов А.М.
Пензенский государственный университет архитектуры и строительства
В материаловедении наибольшее распространение для описания функции отлика и прогнозирования свойств
материалов получили:
- регрессионные модели 
(зависимость отклика
от количественных факторов 
и ошибок 
наблюдения отклика)
- модели дисперсионного анализа ( изучается
зависимость отклика от качественных факторов и ошибок наблюдений отклика:
,
- дискретные
переменные, обычно целочисленные);
- методы ковариационного анализа (сочетание элементов регрессионного и
дисперсионного анализа; учитываются воздействия на отклик как количественных,
так и качественных факторов).
На практике чаще всего используются полиномиальные
модели:
– модель регрессионного анализа первого порядка:
;
– квадратичная модель:
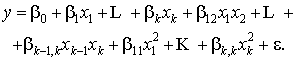
Адекватность модели проверяется по известному
-критерию Фишера.
Возможности практического
использования полученных моделей существенно определяются:
- априорным ранжированием факторов;
- выбором размахов (разности между максимальным
и минимальным натуральными значениями факторов), определяющих границы области варьирования факторов;
- выбором интервалов варьирования факторов в факторном пространстве (половина
размаха варьирования фактора 
; задает область 
действия для данного
плана);
- удачным выбором функции отклика (зависимость математического ожидания
отклика от факторов 
; параметры
модели 
априори неизвестны и
подлежат определению из эксперимента).
В полиномиальном уравнении
регрессии эффекты взаимодействия факторов (зависимости изменения эффекта
одного фактора от уровней других факторов) определяются параметрами при членах,
включающих произведения факторов (парные взаимодействия – 
, тройные – 
и т.д.).
Приведенный подход использовался при исследованиях для прогнозирования свойств эпоксидных
композитов на аппретированном наполнителе [4] (табл.1; на основе отходов
производства оптического стекла (ОПОС) и технического углерода (ТУ)).
Предварительное ранжирование факторов, выбор размахов и интервалов их
изменения, эффективный выбор функции отклика осуществлялись на основе
когнитивного моделирования [5], а также с учетом данных экспертных оценок. В качестве функций отклика
последовательно рассматривались предел прочности (МПа) при сжатии эпоксидного
связующего (ЭС) на основе отходов производства оптического стекла и технического
углерода соответственно. Были получены модели:
;
,
где x1, x2 –
кодированные значения объемной степени наполнения и расчётной толщины слоя
аппрета (ЭС на основе ОПОС или ТУ соответственно).
Для всех исследованных составов экстремальные значения
предела прочности при сжатии достигаются при промежуточных значениях
варьируемых факторов; областью наиболее интенсивных структурных трансформаций в
ЭС на основе ОПОС определяется неравенствами 
и 
.
Таблица 1.
|
ЭС, наполненное
аппретированным ОПОС |
|||
|
№ серии |
Объемная степень наполнения |
Расчётная толщина слоя, нм |
|
|
1 |
0,527 |
6,4 |
|
|
2 |
0,173 |
6,4 |
|
|
3 |
0,527 |
1,1 |
|
|
4 |
0,173 |
1,1 |
|
|
5 |
0,35 |
7,5 |
|
|
6 |
0,35 |
0 |
|
|
7 |
0,6 |
3,75 |
|
|
8 |
0,1 |
3,75 |
|
|
9 |
0,475 |
3,75 |
|
|
10 |
0,225 |
3,75 |
|
|
ЭС, наполненное техническим углеродом и
модифицированное фторхлоруглеродными жидкостями (ФХУЖ) |
|||
|
№ серии |
Объемная степень наполнения |
Концентрация ФХУЖ, % |
|
|
11 |
0,221 |
2,56 |
|
|
12 |
0,08 |
2,56 |
|
|
13 |
0,221 |
0,44 |
|
|
14 |
0,08 |
0,44 |
|
|
15 |
0,15 |
3 |
|
|
16 |
0,15 |
0 |
|
|
17 |
0,25 |
1,5 |
|
|
18 |
0,05 |
1,5 |
|
|
19 |
0,2 |
1,5 |
|
|
20 |
0,1 |
1,5 |
|
Полученные зависимости являются двуэкстремальными (отражают структурные трансформации
в эпоксидном связующем). Для связующего на основе ТУ характерны несколько
меньшие по сравнению с составами, наполненными ОПОС, значения предела прочности
при сжатии. Управление прочностью ЭС на основе
тонкодисперсного ОПОС целесообразно аппретированием наполнителя (позволяет
повысить прочность на 7...12%). При малой дисперсности наполнителя
аппретирование поверхности устраняет недостаток наполнителя.