ЭКСПЕРИМЕНТАЛЬНЫЕ МОДЕЛИ КОМПОЗИТОВ

Пчелинцев И.А., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Установление эмпирической зависимости сводится к проведению по данным экспериментальным точкам некоторой кривой (не ломаной), которая проходила бы как можно ближе к истинной функциональной зависимости.

Значению аргумента соответствует истинное значение измеряемой величины , а в результате измерения вместо получим случайную величину . Так как ошибки измерения величины распределены по нормальному закону с математическим ожиданием, равным, и со средним квадратическим отклонением (характеризует ошибку измерения), то случайная величина будет распределена по нормальному закону:

, ().

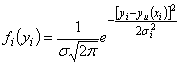Таким образом, в результате ряда измерений произошло следующее событие B: случайные величины () приняли совокупность значений . Тогда установление эмпирической зависимости сводится к подбору математических ожиданий случайных величин , равных , чтобы вероятность события B была максимальна (принцип максимального правдоподобия). Оказывается, если точность измерения при всех одинакова и равна s, то, для того чтобы совокупность наблюдённых значений была наивероятнейшей, нужно выбрать функцию так, чтобы сумма квадратов отклонений наблюдённых значений от была минимальной:

.

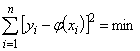Способ согласования кривой и экспериментальных точек, при котором выполняется это условие, носит название метода наименьших квадратов. Если из соображений, связанных с существом изучаемого явления или просто с внешним видом наблюдённой зависимости (расположения точек на плоскости), выбран общий вид функции , зависящий от нескольких числовых параметров , и требуется выбрать так, чтобы выполнялось условие

,

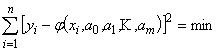то значения определятся из условий:

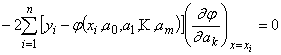
или

.

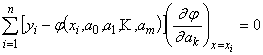Составление и решение этой системы упрощается в случае, когда функция линейна относительно параметров. Тогда справедливо:

;

...

.

; ; ...; .

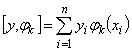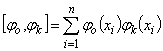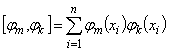В частном случае при сглаживании полиномом коэффициенты определятся из системы уравнений:

;

;

…

.

Рассмотренный подход использовался для установления связи между коэффициентами пластичности k_пл и структуры k_стр эпоксидных композитов (табл.1) . Из расположения экспериментальных точек на плоскости при определении аналитической зависимости ограничились линейной зависимостью

k_стр = a₀ + a₁ k_пл, (=k_пл, = k_стр).

Таблица 1.

kпл	0,08	0,43	0,47	0,51	0,52	0,6	0,7	0,9	0,93	1,4
kстр	16,1	13,2	14,8	14,2	13,8	14,2	7,8	14,5	15	5,4

Искомая зависимость определилась в виде ; возможность ограничиться линейной корреляционной связью между k_стр и k_пл следует из = – 0,68.

Так же определялась зависимость влияния содержания водорода H [вес. ч.] в бетоне на толщину [см] защиты при расчёте, исходя из допустимой дозы излучений синхроциклотрона X_д , допустимого потока X_п при кратности ослабления 10⁷ раз и плотности бетона 2350 кг/м³ (табл.2).

Таблица 2

H, вес. ч.	0,1	0,35	0,61	0,81	1,09
Xд, см	1005	991	983	980	975
Xп, см	1133	1095	1077	1069	1060

Здесь линейная интерпретация дает большую погрешность. Поэтому были определены параметры квадратичной зависимости X_д от H . В соответствии с предыдущим была получена следующая искомая аналитическая зависимость в виде:

.

Для получения аналитических зависимостей часто используются и методы математического планирования эксперимента (полно- и дробно-факторные планы эксперимента, позволяющие получить интерполяционные полиномы во всем рассматриваемом факторном пространстве или его локальной области при существенном сокращении числа опытов в эксперименте).

Литература

1. Будылина Е.А., Гарькина И.А., Данилов А.М., Махонин А.С.Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. -2013. -№ 5. С. 42-45.
2. Будылина Е.А., Гарькина И.А., Данилов А.М., Пылайкин С.П. Подходы к многокритериальности сложных систем / Молодой ученый. -2013. -№6. С. 40-43.
3. Будылина Е.А., Гарькина И.А., Данилов А.М., Сухов Я.И. Некоторые подходы к анализу и синтезу сложных систем / «Молодой ученый. - №10(57), 2013. – с.105-107.