Мустафаев А. П.

к.ф.-м.н., доцент ИПКПР АО

Утеджанова Б. К.

К.п.н., доцент Казахского экономического университета им. Т. Рыскулова

г. Алматы, Казахстан

ОТ ПРОСТОГО - К СЛОЖНОМУ

ЮНЕСКО провозгласило XXI столетие - веком компьютеризации, что актуализировало роль математики. Особенно велико значение математики в развитии современной физики, астрономии, химии. Значительное место занимает математика в экономике, биологии, медицине.

В особенности она связана с разработкой эффективных математических методов, алгоритмов с применением компьютера.

Даже юристы и историки берут на свое вооружение «Математические методы». Кроме прикладного значения математических методов, изучение конкретных теоретических основ Высшей математики - развивает логику, абстрактное мышление учащихся и молодежи.

А также математические знания, приобретенные школьниками при изучении элементарной математики понадобятся при изучении и понимании разделов Высшей математики и специальные курсы фундаментальной математики.

Например, в программе средней школы часто встречаются задания следующего вида:

1. Вычислить:

а) +++++ +

б) +++ +

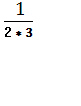2. Упростиь выражение:

а)++ +

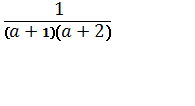б)++ +

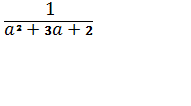3. Решить уравнение:

а) + + … +

б) ++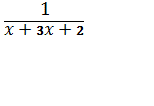 + =0

4. Найти первообразную функции:

а) f(x) =

б) Вычислить интеграл:

В первых заданиях ученики решают, приводя дроби к общему знаменателю, а после прохождения темы: «Разложение рациональной дроби на простые дроби», ученики поймут, что используя эту методику, заданную дробь можно представить в виде:

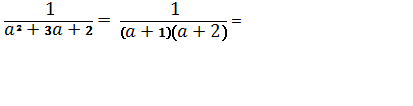
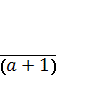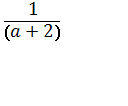= - , - , то получим:

++ +- =

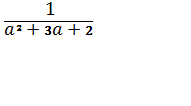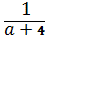Все это дает ученикам быстро решить уравнения в той или иной форме, найти первообразную от рациональных функций и повышает интерес к математике.

Рассмотрим некоторые задания из теории комплексного переменного и операционного исчисления, которые необходимо использовать теорию разложения рациональных дробей на простейшие.

1) Разложить функцию

f(z)=

в ряд Лорана.

Для этого, необходимо представить функцию f(z) в виде:

f(z)= + .

Далее проводятся необходимые исследования.

2) Вычислить интеграл: C:+=

.

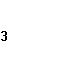
C

3) Найти оригинал функции:

F(p)=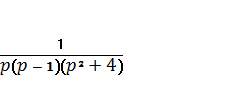

4) Решить задачу Коши:

+x=f(t)

x(0)= , если f(t) =µ(t) - 2 µ(t-1) + µ(t-2),

применяя преобразования Лапласса, с учетом начальных условий, уравнение примет вид:

+1)X(p) =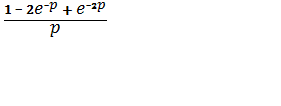 , отсюда X(p) = - ,

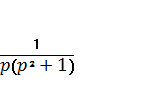где

=.

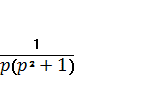Отсюда видим связь и важность простейших тем элементарной математики со сложными разделами высшей математики, поэтому учителя предметники начальных классов должны знать, не только теорию математики на уровне 9-го класса, но и практическое применение и прикладные аспекты. Учителя старших классов обязаны знать на уровне программы высшей математики.

Литература:

1.Груденев Я.И. Совершенствование методики работы учителя математики: Кн. Для учителя.- М.: Просвещение, 2000.-224с.

2.Углубленное изучение алгебры и анализа. Пособие для учителей. Сост.: С.И. Шварцбурд, О.а. Боковнев. М., «Просвещение», 1997.