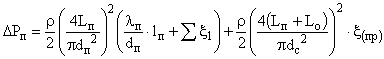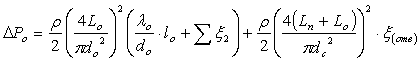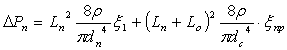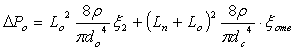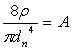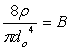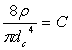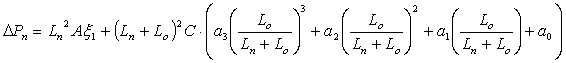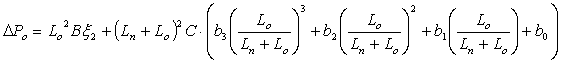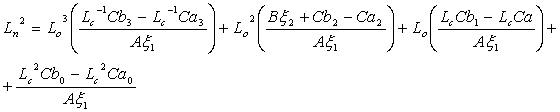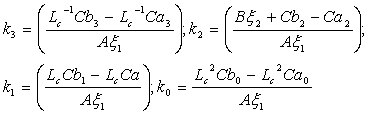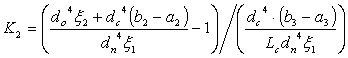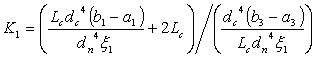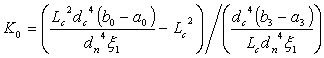Д.т.н. Азаров Валерий Николаевич,

к.т.н. Боровков Дмитрий Павлович

Волгоградский государственный архитектурно-строительный университет,

Россия

к.т.н. Чичиров Константин Олегович

Пензенский государственный университет архитектуры и строительства, Россия

проведения прямого и обратного аэродинамического расчета систем аспирации СУШИЛЬНОГО ОБОРУДОВАНИЯ ПРЕДПРИЯТИЙ СТРОИТЕЛЬНОЙ ИНДУСТРИИ с закруткой потока в воздуховодах

В процессе эксплуатации систем аспирации в горизонтальных и наклонных воздуховодах в ряде случаев возникают пылевые отложения. При этом происходит уменьшение живого сечения аспирационного потока и повышение аэродинамического сопротивления аспирационной сети, что со временем может привести к разрегулировке и прекращению работы системы аспирации. Перспективным методом предотвращения образования пылевых отложений в воздуховодах систем аспирации является закрутка аспирационного потока [1].

Закрученный газовый поток характеризуется повышенной способностью приводить в движение и переносить твердые пылевидные частицы, что позволяет улучшить условия перемещения пылевидных материалов и предотвратить образование пылевых отложений в воздуховодах систем аспирации без внесения существенных изменений в аспирационную сеть и применения сложного и дорогостоящего оборудования. Однако внедрение систем аспирации с закрученными потоками в производство строительных материалов на настоящий момент сдерживается отсутствием необходимых технических решений, а также методов проектирования и расчета.

При проведении обратного аэродинамического расчета неразветвленных аспирационных и вентиляционных сетей, как правило, используется метод характеристик, суть которого состоит в решении системы уравнений состоящей из уравнения характеризующего изменение потерь давления проходящего по воздуховоду газового (воздушного) потока в зависимости от объема проходящего газа и уравнения характеризующего напорную характеристику тягодутьевого устройства. При составлении уравнений используются общепринятые зависимости, характеризующие аэродинамическое сопротивление различных элементов вентиляционных сетей и технические характеристики тягодутьевых устройств, поэтому применение метода характеристик для неразветвленных сетей не представляет затруднений.

Иначе обстоит ситуация с обратным аэродинамическим расчетом разветвленной сети. Основным затруднением при этом является сложности связанные с определение коэффициентов местного сопротивления тройников на проход и ответвление, в виду того, что их значения зависят от соотношения расходов в параллельных участках сети, определение которых как раз и является целью обратного аэродинамического расчета.

Согласно стандартной методике [2], коэффициенты местного сопротивления тройника на проход и ответвление x_пр и x_отв определяются на основании представленных в табличной форме экспериментальных данных, как функция от разности диаметров прохода и ствола; разности диаметров ответвления и ствола; угла между проходом и ответвлением и соотношения расходов ответвления и ствола. Очевидно, что при обратном расчете изменяется только соотношение расходов, а конструктивные характеристики тройника постоянны, поэтому представляется рациональным в целях автоматизации расчета охарактеризовать к.м.с. тройников одномерными регрессионными зависимостями вида для различных сочетаний конструктивных факторов. Практика показывает что данные, предлагаемые стандартной методикой для определения к.м.с. проходов и ответвлений для всех представленных сочетаний конструктивных факторов адекватно апроксимируются полиномами третьей степени вида b₃*x³+b₂*x²+b₁*x+b₀ [3].

Соответствующие зависимости, характеризующие потери давления на параллельных участках имеют вид:

		(1)
		(2)
где:	Lп, dп, lп, Уо1 – соответственно расход, диаметр, коэффициент аэродинамического сопротивления и сумма к.м.с. на участке присоединенном к «проходу» тройника, а Lо, dо, lп, Уо2 – соответственно тоже для участка присоединенного к «ответвлению»; dс – диаметр ствола; опр, оотв – соответственно к.м.с. прохода и ответвления тройника.

В виду того, что значение коэффициента аэродинамического сопротивления участка λ практически не изменяется при изменении расхода газа в процессе обратного аэродинамического расчета оно принимается постоянной величиной, и вычисляется для соответствующего участка исходя из условия равенства расходов прохода и ответвления (L_п =L_о).

Первые члены уравнений (1) и (2) выражаются в виде произведения динамического давления на сумму коэффициентов местных сопротивлений и приведенного коэффициента местного сопротивления по длине участка :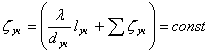

		(3)
		(4)
где:	о1, о2 – суммарные коэффициенты местных сопротивлений участков присоединенных соответственно к притоку и ответвлению.

Из (3) и (4) следует, что в условиях обратного аэродинамического расчета, при котором переменными являются только величины расходы газа в ветвях сети L_п и L_о и коэффициент местного сопротивления тройника на проход и ответвление о_пр, о_отв. Пусть:

Тогда:			(5)
			(6)

При подстановке полиномиальных зависимостей, характеризующих ζ_пр, ζ_отв в (5) и (6) имеем:

		(7)
		(8)
где:	ai и bi – соответствующие коэффициенты уравнений регрессии, характеризующих коэффициенты местного сопротивления тройника на проход и ответвление.

Поскольку суммарный расход (расход в стволе) задается на стадии предшествующей обратному расчету величина L_с = L_п + L_о является постоянной, заменяя суммарный расход параллельных участов расходом ствола, и раскрывая скобки, имеем:

		(9)
		(10)
где:	Lс – расход газа в «стволе»

Приравняв зависимости (9) и (10), характеризующие аэродинамическое сопротивление параллельных участков, выразив расход прохода через расход ответвления, и сгруппировав члены уравнения по степеням расхода L_о получим уравнение:

(11)

Так как сумма расходов прохода и ответвления составляет постоянную величину (расход ствола) и задана на начальном этапе расчета, расход прохода может быть выражен как разность расхода ствола и расхода ответвления. При этом имеем:

(Lс-Lо)^2=k3Lo^3+k2Lo^2+k1Lo+k0		(12)
где:

Или:

k3Lo^3+(k2-1)Lo^2+(k1+2 Lс) Lo+(k0- Lс^2) =0

(13)

Для удобства решения полученного уравнения оно путем почленного деления постоянных коэффициентов на k₃, приводится к виду:

Lo^3+K2Lo^2+K1 Lo+K0 =0, где	(14)
	(15)
	(16)
	(17)

Оценка полученного уравнения (14) с учетом величины его коэффициентов, определяемых по формулам (15), (16), (17) показывает, что во всех случаях уравнение имеет два комплексно-сопряженных и один действительный корень, очевидно являющийся искомым значением расхода в ответвлении L_о. Значение L_п при этом определяется как разность расхода ствола и полученного расхода в ответвлении.

Выводы:

1. Внедрение систем аспирации с закрученными потоками, позволяющими предотвратить образование пылевых отложений в воздуховодах в настоящий момент сдерживается отсутствием методов прямого и обратного аэродинамического расчета.

2. Применение зависимостей характеризующих соотношение коэффициентов аэродинамического сопротивления осевого и закрученного потоков в зависимости от осредненной интенсивности закрутки потока позволяет использовать метод характеристик для проведения прямого и обратного аэродинамического расчета аспирационных сетей.

3. Использование полиномов третьей степени позволяющее адекватно аппроксимировать значения коэффициентов местного сопротивления тройников-закручивателей сводит обратный аэродинамический расчет параллельных участков к решению уравнения третьей степени.

Литература:

1. Применение закрученных потоков в системах аспирации строительной отрасли / В.Н.Азаров, Д.П. Боровков // Объединенный научный журнал. – 2003. – №5 (63). – С. 102 - 104.

2. Внутренние санитарно-технические устройства. В 3ч. Ч. 3. Вентиляция и кондиционирование воздуха / Богословский В.Н., Пирумов А.И., Посохин В.Н. и др.; Под ред. Павлова Н.Н. и Шиллера Ю.И. – 4-е изд., перераб. и доп. – М.: Стройиздат, 1992. – (Справочник проектировщика). – 392 с.: ил.

3. Об обратном аэродинамическом расчёте разветвлённых систем аспирации [Текст] / В. Н. Азаров, А. О. Юдочкина, Д. П. Боровков// Объединённый научный журнал. – 2006. - №14. – С.40-43.