1. Постановка задачи
нейронного управления
Одной из ключевых
проблем современного развития транспортной инфраструктуры России является
проблема управления транспортными системами на всех этапах их жизненного цикла (проектирование,
производство, эксплуатация). Проблема управления транспортными системами, в
свою очередь, сводится к решению задач управления техническими
(организационно-техническими) системами и технологическими процессами [1].
Рассмотрим
технологический процесс (ТП), состоящий из 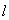 взаимодействующих
технологических модулей (ТМ). ТМ имеют общую, известную заранее структуру и
отличаются только переходами от j-го входа к i-ому
выходу ТП. Полагаем, что каждый ТМ выполняет определенную функцию сложного ТП,
и описывается последовательным соединением линейной дифференциальной системы
(линеаризованной на интервале дискретизации (наблюдения) нелинейной системы
обыкновенных дифференциальных уравнений) объекта и нелинейного безынерционного
преобразователя (НБП) – однослойного персептрона (искусственного нейрона).
Такие ТМ образуют класс абсолютно устойчивых нелинейных систем [2].
взаимодействующих
технологических модулей (ТМ). ТМ имеют общую, известную заранее структуру и
отличаются только переходами от j-го входа к i-ому
выходу ТП. Полагаем, что каждый ТМ выполняет определенную функцию сложного ТП,
и описывается последовательным соединением линейной дифференциальной системы
(линеаризованной на интервале дискретизации (наблюдения) нелинейной системы
обыкновенных дифференциальных уравнений) объекта и нелинейного безынерционного
преобразователя (НБП) – однослойного персептрона (искусственного нейрона).
Такие ТМ образуют класс абсолютно устойчивых нелинейных систем [2].
Уравнения 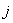 -го ТМ (
-го ТМ (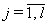 ) имеют вид
) имеют вид
Индекс 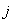 для краткости записей
переменных и параметров системы уравнений (1) – (3) опускаем. В дальнейшем
полагаем, что система (1) должна удовлетворять требованиям существования и
единственности решения;
для краткости записей
переменных и параметров системы уравнений (1) – (3) опускаем. В дальнейшем
полагаем, что система (1) должна удовлетворять требованиям существования и
единственности решения; 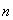 - вектор неконтролируемых возмущений
- вектор неконтролируемых возмущений 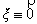 .
.
В формулах (1) – (3) обозначено: 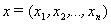 –
– 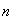 -мерный вектор состояния
-мерный вектор состояния 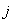 -го ТМ,
-го ТМ, 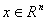 ;
;
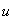 – управление
– управление 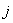 -ым ТМ (измеряемый скалярный вход системы (1)),
-ым ТМ (измеряемый скалярный вход системы (1)), 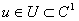 ;
;
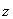 – наблюдение
– наблюдение 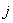 -ым ТМ (измеряемый скалярный выход системы (1)),
-ым ТМ (измеряемый скалярный выход системы (1)),  ;
;
 – постоянная
параметрически неопределенная матрица Якоби размерности
– постоянная
параметрически неопределенная матрица Якоби размерности 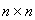 ;
;
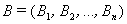 – постоянный вектор
настраиваемых параметров НБП размерности
– постоянный вектор
настраиваемых параметров НБП размерности  ;
;
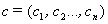 – вектор-столбец задаваемых параметров наблюдения (регрессии)
размерности
– вектор-столбец задаваемых параметров наблюдения (регрессии)
размерности 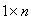 ;
;
 – скалярный
параметрический регулятор;
– скалярный
параметрический регулятор;
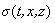 – скалярная функция
активации (ФА) однослойного персептрона, получаемая нелинейным преобразованием
– скалярная функция
активации (ФА) однослойного персептрона, получаемая нелинейным преобразованием 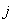 -ого управления
-ого управления  и
и 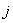 -ого наблюдения
-ого наблюдения 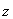 .
.
Структура однослойной нейронной сети,
параметрически адаптированной под  -ый ТМ, представлена на Рисунке 1.
-ый ТМ, представлена на Рисунке 1.
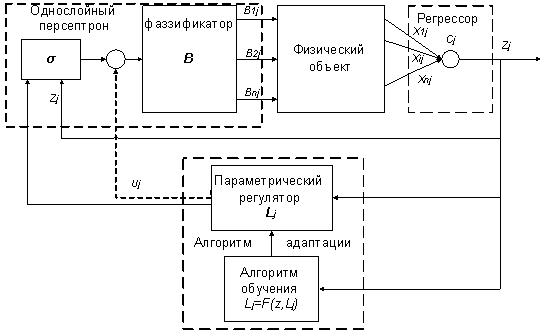
Рис. 1. – Структура
однослойной нейронной сети, параметрически адаптированной под 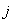 -ый ТМ.
-ый ТМ.
На Рис. 1 сплошными линиями обозначена
структура однослойной НС с нелинейностью в «прямой цепи». Предлагаемая
структура отличается от традиционной схемы адаптивного регулятора (АР) наличием
НБП и положительной жесткой обратной связи по скалярному выходу 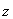 . Данная структура НС добавлена пунктирной линией и
сумматором – «цепью внутренней обратной связи» по скалярному входу
. Данная структура НС добавлена пунктирной линией и
сумматором – «цепью внутренней обратной связи» по скалярному входу 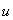 [2].
[2].
2. Свойства функции активации
ФА определяет архитектуру НС. Однозначных
рекомендаций по выбору ФА в настоящее время не существует. В режиме обучения of-line наиболее эффективен алгоритм обратного распространения ошибки сигнала
и следующие ФА: гиперболическая тангенциальная, линейная и логическая
сигмоидальная функции активации [1].
В режиме on-line (оперативное обучение и управление), когда НС работает в реальном
времени и выполняет функции адаптивного регулятора, будем полагать, что ФА
удовлетворяет условиям [2]
|
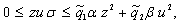
|
(4)
|
где  ,
,  ,
, 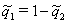 ,
, 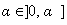 ,
, 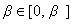 ;
;  – корректируемые на
интервалах наблюдения нечеткие коэффициенты, определяющие перераспределение
сигналов от входа к выходу и от выхода к входу (режим работы НС);
– корректируемые на
интервалах наблюдения нечеткие коэффициенты, определяющие перераспределение
сигналов от входа к выходу и от выхода к входу (режим работы НС); 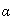 ,
,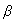 – весовые коэффициенты соответствующей физической
размерности (ед.) при переменных в правой части ограничений на
– весовые коэффициенты соответствующей физической
размерности (ед.) при переменных в правой части ограничений на 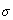 .
.
НБП 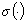 определяется правой
частью выражения (4)
определяется правой
частью выражения (4)
|
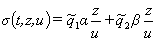 . .
|
(5)
|
Функция (5) имеет две особые точки z=0; u=0.
Предварительно будем считать их изолированными [3]. Так как наблюдение 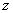 и уравнение
и уравнение 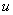 – скалярные функции, то
с учетом (3) НБП (5) можно представить в виде
– скалярные функции, то
с учетом (3) НБП (5) можно представить в виде
|
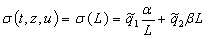 . .
|
(6)
|
Зависимость 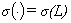 при фиксированных
при фиксированных  ,
, 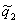 показана на Рисунке
2.
показана на Рисунке
2.
Исследуя свойства функции 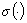 (формулы (5), (6)),
можно заметить, что функция
(формулы (5), (6)),
можно заметить, что функция 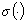 : 1). Знакоопределенная:
: 1). Знакоопределенная: 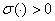 при
при 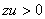 (
(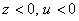 или
или 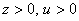 );
); 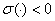 при
при 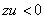 (
(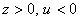 или
или 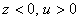 ) .
) .
2).
Имеет особую точку 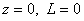 , в которой происходит разрыв первого рода
, в которой происходит разрыв первого рода
3). Имеет две точки экстремума:
точку максимума 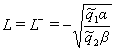 и точку минимума
и точку минимума 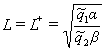 . В точках экстремума функция
. В точках экстремума функция 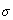 принимает значения:
принимает значения:
|
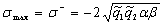 , ,
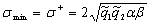 . .
|
|
4). Имеет
нечетно-симметрическую форму: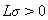 при
при 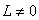 . Действительно, эта функция изменяет знак только при
условии
. Действительно, эта функция изменяет знак только при
условии 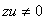 . При
. При 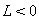 (
( ) функция
) функция 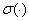 определяется в III квадранте Рис. 2 и отрицательна:
определяется в III квадранте Рис. 2 и отрицательна: 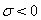 . При
. При 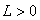 ФА вычисляется в I квадранте и положительна:
ФА вычисляется в I квадранте и положительна:  . Параметр
. Параметр  , так как
, так как 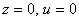 – особые точки.
– особые точки.
5). При 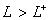 и
и  функция
функция 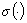 близка к линейной c коэффициентами наклона прямых
близка к линейной c коэффициентами наклона прямых 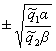 в первом и третьем квадранте Рисунка 2.
в первом и третьем квадранте Рисунка 2.
НБП 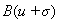 (формула (1)) для
(формула (1)) для 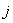 -го ТМ в теории НС и нечетких множеств называется однослойным
персептроном с ненулевым смещением или фаззификатором, вектор-строка
-го ТМ в теории НС и нечетких множеств называется однослойным
персептроном с ненулевым смещением или фаззификатором, вектор-строка 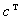 – регрессором или дефаззификатором [1].
– регрессором или дефаззификатором [1].
При адаптивном подходе считается, что
существует устойчивая внутренняя структура физического объекта [3], но
неизвестны его параметры (коэффициенты матрицы 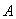 ). Относительно нелинейности указаны частичные свойства
характеристики
). Относительно нелинейности указаны частичные свойства
характеристики 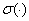 . Кроме того, неизвестен вектор
. Кроме того, неизвестен вектор 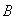 настраиваемых весовых
коэффициентов однослойного персептрона.
настраиваемых весовых
коэффициентов однослойного персептрона.
Требуется осуществить оперативное
управление 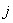 -ым ТМ с помощью адаптивного параметрического нейрорегулятора
-ым ТМ с помощью адаптивного параметрического нейрорегулятора
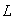 .
.
В
основу предлагаемого подхода положена параллель со схемой адаптивного
управления с самонастройкой: НС настраивает параметры управления, задающие
работу обычного контроллера, таким образом, чтобы выходной сигнал 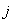 -го ТМ поддерживался как можно ближе к желаемому:
-го ТМ поддерживался как можно ближе к желаемому: 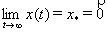 . Такое управление
. Такое управление 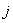 -ым ТМ называется стабилизирующим [3]. Задача синтеза
адаптивного параметрического нейрорегулятора решается в три этапа [2]:
исследуется выбранный класс нелинейных систем на устойчивость; синтезируется
стабилизирующее управление
-ым ТМ называется стабилизирующим [3]. Задача синтеза
адаптивного параметрического нейрорегулятора решается в три этапа [2]:
исследуется выбранный класс нелинейных систем на устойчивость; синтезируется
стабилизирующее управление 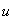 , обеспечивающее цель адаптации:
, обеспечивающее цель адаптации: 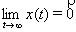 ; по условиям устойчивости инициализируются параметры НС.
; по условиям устойчивости инициализируются параметры НС.
3. Устойчивость
системы по Ляпунову
Устойчивость рассматривается как свойство
свободного движения системы (1) после начального отклонения ее, вызванного
какими-либо причинами. Невозмущенное движение 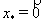 определяется нулевым
решением системы (1).
определяется нулевым
решением системы (1).
Аналитическое определение понятия
устойчивости по Ляпунову формулируется следующим образом [4].
Определение. Нулевое решение системы (1)
устойчиво, если при заданном сколь угодно малом 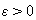 существует такое
существует такое  , зависящее от
, зависящее от 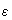 , что при начальных условиях
, что при начальных условиях  , для решения на интервале
, для решения на интервале 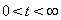 выполняется условие
выполняется условие 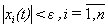 .
.
Если условия определения соблюдены и выполняется условие 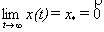 , то нулевое решение системы (1) асимптотически устойчиво.
, то нулевое решение системы (1) асимптотически устойчиво.
Зависимость 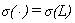 при фиксированных
при фиксированных 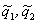 представлена на Рис. 2.
представлена на Рис. 2.
Теорема. Если для системы уравнений (1) - (3) существует положительная знакоопределенная
функция 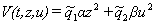 , то при НБП вида (6) производная
, то при НБП вида (6) производная 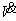 от этой функции является
тоже знакоопределенной, но противоположного знака, если одновременно выполняются
условия
от этой функции является
тоже знакоопределенной, но противоположного знака, если одновременно выполняются
условия
|
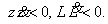 
|
(7)
|
При этом решение системы (1) асимптотически устойчиво: 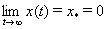 .
.
Доказательство. Выбираем в качестве функции Ляпунова правую часть
неравенства (4):  . С учетом уравнения регулятора (3) определим производную
функции Ляпунова
. С учетом уравнения регулятора (3) определим производную
функции Ляпунова
Анализ последнего выражения показывает, что 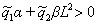 ,
,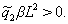 Тогда для отрицательной знакоопределенности
Тогда для отрицательной знакоопределенности 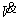 обязательно выполнение условий (7) теоремы. Условия
устойчивости (7) не зависят от конкретной нечетно-симметрической формы НБП
обязательно выполнение условий (7) теоремы. Условия
устойчивости (7) не зависят от конкретной нечетно-симметрической формы НБП 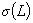 . Поэтому они одновременно являются условиями абсолютной
устойчивости системы (1) - (3) [4]. Вследствие того, что
. Поэтому они одновременно являются условиями абсолютной
устойчивости системы (1) - (3) [4]. Вследствие того, что 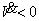 , функция Ляпунова будет монотонно убывающей функцией с нижним
пределом
, функция Ляпунова будет монотонно убывающей функцией с нижним
пределом 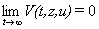 . Следовательно, имеет место достаточное условие
асимптотической устойчивости:
. Следовательно, имеет место достаточное условие
асимптотической устойчивости: 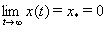 .
.
Поскольку точки 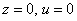 – особые точки, то
достаточное условие асимптотической устойчивости приближенно выполняется в
некоторой области, ограниченной вертикальными
– особые точки, то
достаточное условие асимптотической устойчивости приближенно выполняется в
некоторой области, ограниченной вертикальными 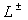 и горизонтальными
и горизонтальными 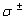 асимптотами функции
асимптотами функции 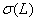 (Рисунок 2). Эта
область называется областью скользящих режимов [5]. При
(Рисунок 2). Эта
область называется областью скользящих режимов [5]. При 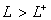 и
и 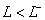 функция
функция 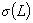 близка к линейной зависимости,
и, следовательно, параметрический регулятор
близка к линейной зависимости,
и, следовательно, параметрический регулятор 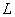 в этих областях
изменения аргумента является квазилинейным.
в этих областях
изменения аргумента является квазилинейным.
В области скользящих режимов необходимо обеспечить выполнение условий
(7) теоремы. Первое условие устойчивости в (7) на практике реализуется через
измерение выходной величины 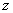 и её производной.
Второе условие в (7) теоремы выполняется через алгоритмически организованную процедуру
параметрического синтеза стабилизирующего управления методом скоростного градиента.
и её производной.
Второе условие в (7) теоремы выполняется через алгоритмически организованную процедуру
параметрического синтеза стабилизирующего управления методом скоростного градиента.
4. Параметрический синтез стабилизирующего управления методом скоростного
градиента
Подстройка НС под эталонную модель (желаемый выходной сигнал) 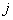 -го ТМ может осуществляться различными градиентными методами.
В качестве эффективного алгоритма обратного распространения в статье
предлагается использовать метод скоростного градиента (МСГ) [3].
-го ТМ может осуществляться различными градиентными методами.
В качестве эффективного алгоритма обратного распространения в статье
предлагается использовать метод скоростного градиента (МСГ) [3].
Формулировка задачи синтеза
стабилизирующего управления по МСГ сводится к следующему.
Состояние 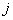 -го ТМ –
-го ТМ – 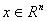 , управление
, управление 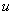 – скалярное,
наблюдается скалярная величина
– скалярное,
наблюдается скалярная величина 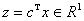 . Эволюцию
. Эволюцию 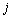 -го ТМ описывает дифференциальная система (
-го ТМ описывает дифференциальная система ( ), где измеряемая кусочно-дифференцируемая функция
), где измеряемая кусочно-дифференцируемая функция 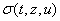 является аддитивной
добавкой к скалярному управлению
является аддитивной
добавкой к скалярному управлению  и подчинена
ограничению вида (4),
и подчинена
ограничению вида (4),  – постоянный
– постоянный 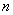 - вектор
настраиваемых входных параметров. Управление линейно зависит от наблюдаемой
величины:
- вектор
настраиваемых входных параметров. Управление линейно зависит от наблюдаемой
величины: 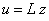 .
.
Матрица 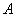 и вектор
и вектор 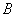 заранее неизвестны.
Вектор
заранее неизвестны.
Вектор 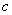 , учитывающий «вклады» переменных состояния
, учитывающий «вклады» переменных состояния  в наблюдение
в наблюдение  , задается.
, задается.
Требуется синтезировать параметрический
регулятор 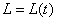 .
.
Цель управления – выполнение условия  – соответствует
минимизации в пределе локального функционала
– соответствует
минимизации в пределе локального функционала 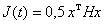 , где
, где 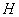 – положительно
определенная, симметрическая матрица размерности
– положительно
определенная, симметрическая матрица размерности 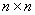 .
.
Для синтеза нелинейного параметрического
регулятора применим схему МСГ в дифференциальной форме [6].
|
Для этого определим полную производную
от локального функционала
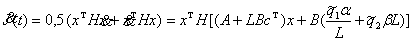
|
|
и вычислим градиент по параметру 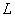
|
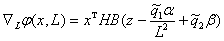 . .
|
|
По схеме МСГ синтезируемый в
дифференциальной форме нелинейный скалярный регулятор имеет вид
|
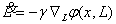 . .
|
(8)
|
Для системы (1), (2), (3) при ограничениях
на ФА типа (4) алгоритм адаптации (обучения) 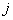 -го ТМ записывается в виде
-го ТМ записывается в виде
|

|
(9)
|
где 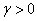 – положительное
число, определяющее скорость убывания градиента по параметру
– положительное
число, определяющее скорость убывания градиента по параметру 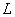 .
.
По постановке задачи процедура управления
должна зависеть только от наблюдаемой величины 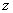 (Рисунок 1). Поэтому
в (9) потребуем соблюдения равенства
(Рисунок 1). Поэтому
в (9) потребуем соблюдения равенства
|
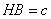 . .
|
(10)
|
Тогда с учетом того, что 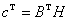 , в окончательном виде получим алгоритм адаптации
, в окончательном виде получим алгоритм адаптации 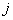 -го ТМ
-го ТМ
|
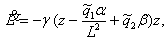
|
(11)
|
где 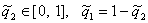 – параметры, определяющие режим работы НС.
– параметры, определяющие режим работы НС.
5. Инициализация начальных условий
Реализация условия устойчивости нулевого
решения уравнений  -го ТМ (условие б) теоремы 1 [2]) для достижения цели
адаптации
-го ТМ (условие б) теоремы 1 [2]) для достижения цели
адаптации  сводится к
инициализации начальных условий алгоритма адаптации (11).
сводится к
инициализации начальных условий алгоритма адаптации (11).
Воспользуемся равенством (10). Матрицу 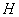 в локальном функционале
в локальном функционале
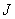 и в формуле (9)
рекомендуется выбирать таким образом, чтобы выполнялось неравенство [3, с. 331]
и в формуле (9)
рекомендуется выбирать таким образом, чтобы выполнялось неравенство [3, с. 331]
|
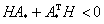
|
(12)
|
где 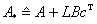 – задаваемая при
некотором
– задаваемая при
некотором 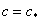 , желаемая гурвицева матрица замкнутой регулятором
, желаемая гурвицева матрица замкнутой регулятором  системы (1), (2),
(3). Матрица
системы (1), (2),
(3). Матрица 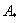 может быть
предварительно идентифицирована (эмулирована в НС) по экспериментальным данным
входo-выходных характеристик замкнутого линейным
регулятором физического объекта.
может быть
предварительно идентифицирована (эмулирована в НС) по экспериментальным данным
входo-выходных характеристик замкнутого линейным
регулятором физического объекта.
Неравенство (12) соответствует второй
лемме Ляпунова об устойчивости движения и указывает класс технических систем,
который алгоритмом адаптации приводится к цели. Этот класс полностью определяется
через параметры алгоритма.
Инициализация начальных условий алгоритма
адаптации (1) сводится к следующему.
1). Используя пакет Mat Lab Toolbox LMI, методом линейного программирования решаем систему
матричных неравенств Ляпунова (12) и определяем матрицу  .
.
2). Задаваясь весами 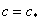 выходных сигналов
выходных сигналов  , из формулы (10) вычисляем параметры вектора
, из формулы (10) вычисляем параметры вектора  НБП:
НБП: 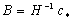 .
.
3). Применяя условие устойчивости б)
теоремы 1 [2], определяем начальное условие 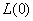 алгоритма адаптации
(11) (
алгоритма адаптации
(11) (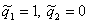 ):
):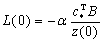 .
.
В последующем начальные условия алгоритма
адаптации (11) уточняются в реальном времени с шагом, равным периоду дискретизации
(интервалу наблюдения) выходного сигнала 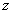 .
.
Альтернативный путь предварительной
инициализации параметров НС по алгоритму обратного распространения –
использование пакета Neural
Toolbox среды Mat Lab [7].
Дальнейшее оперативное обучение и
управление 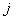 - ым ТМ производится по алгоритму адаптации (11) (
- ым ТМ производится по алгоритму адаптации (11) (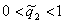 ). При
). При 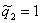 процесс обучения НС
заканчивается. НС работает как обычный
АР.
процесс обучения НС
заканчивается. НС работает как обычный
АР.
Заключение
Таким образом, в статье на основе организации
параметрического управления по методу скоростного градиента разработан
эффективный алгоритм адаптации, позволяющий:
1) ускорить сходимость нейро-нечеткого
управления за счет обучения нейронной сети в реальном времени;
2) применить гибридные сети, в которых
искусственные нейронные сети связываются со структурами адаптивного управления
на основе традиционных технологий;
3) осуществить предварительное обучение и
применить эффективные процедуры инициализации параметров нейронной сети.
Для практической реализации алгоритма
адаптации на базе однослойной нейронной сети достаточно знаний о порядке
дифференциальных уравнений, описывающих физический объект с устойчивой
структурой взаимосвязей между ее элементами.
В отличие от традиционного адаптивного подхода, когда область
устойчивых решений линейной части системы (1) определяется условием 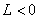 , при организации нейроподобных структур областью допустимых
значений параметра
, при организации нейроподобных структур областью допустимых
значений параметра 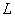 регулятора является
все множество действительных чисел
регулятора является
все множество действительных чисел 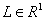 .
.
Литература:
1. Крылов
А.А., Сизых В.Н., Чумак А.Г. Методика структурно-параметрического синтеза
нейросетевой модели продольного движения воздушного транспортного средства //
Журнал «Современные технологии. Системный анализ. Моделирование». – Иркутск:
Изд-во ИрГУПС, 2011. № 1(29). – С. 129-134.
2. Мухопад Ю.Ф., Пашков
Н.Н., Сизых В.Н. Адаптивный подход к нейронному управлению одним классом
абсолютно устойчивых систем. – М.: Изд-во РАЕ, 2011, №8. Ч. 1. – С. 139-147.
3. Срагович В.Г. Адаптивное
управление. – М.: Наука, 1981. – 384 с.
4. Попов Е.П. Теория
нелинейных систем автоматического регулирования и управления. – М.: Наука,
1988. – 256 с.
5. Уткин В.И. Скользящие
режимы и их применение в системах с переменной структурой. М.: Наука, 1974. –
272 с.
6. Фрадков А.Л. Схема
скоростного градиента и ее применение в задачах адаптивного управления. // А и
Т, 1979, № 9. – С. 90-101.
7. Терехов В.А., Ефимов Д.В., Тюкин И.Ю.
Нейросетевые системы управления // Нейроконтроллеры и их применение / Под ред.
А.И. Галушкина. – М.: ИПРЖР, 2002. – 480 с.
![]() взаимодействующих
технологических модулей (ТМ). ТМ имеют общую, известную заранее структуру и
отличаются только переходами от j-го входа к i-ому
выходу ТП. Полагаем, что каждый ТМ выполняет определенную функцию сложного ТП,
и описывается последовательным соединением линейной дифференциальной системы
(линеаризованной на интервале дискретизации (наблюдения) нелинейной системы
обыкновенных дифференциальных уравнений) объекта и нелинейного безынерционного
преобразователя (НБП) – однослойного персептрона (искусственного нейрона).
Такие ТМ образуют класс абсолютно устойчивых нелинейных систем [2].
взаимодействующих
технологических модулей (ТМ). ТМ имеют общую, известную заранее структуру и
отличаются только переходами от j-го входа к i-ому
выходу ТП. Полагаем, что каждый ТМ выполняет определенную функцию сложного ТП,
и описывается последовательным соединением линейной дифференциальной системы
(линеаризованной на интервале дискретизации (наблюдения) нелинейной системы
обыкновенных дифференциальных уравнений) объекта и нелинейного безынерционного
преобразователя (НБП) – однослойного персептрона (искусственного нейрона).
Такие ТМ образуют класс абсолютно устойчивых нелинейных систем [2].![]() -го ТМ (
-го ТМ (![]() ) имеют вид
) имеют вид![]() для краткости записей
переменных и параметров системы уравнений (1) – (3) опускаем. В дальнейшем
полагаем, что система (1) должна удовлетворять требованиям существования и
единственности решения;
для краткости записей
переменных и параметров системы уравнений (1) – (3) опускаем. В дальнейшем
полагаем, что система (1) должна удовлетворять требованиям существования и
единственности решения; ![]() - вектор неконтролируемых возмущений
- вектор неконтролируемых возмущений ![]() .
.![]() –
– ![]() -мерный вектор состояния
-мерный вектор состояния ![]() -го ТМ,
-го ТМ, ![]() ;
;![]() – управление
– управление ![]() -ым ТМ (измеряемый скалярный вход системы (1)),
-ым ТМ (измеряемый скалярный вход системы (1)), ![]() ;
;![]() – наблюдение
– наблюдение ![]() -ым ТМ (измеряемый скалярный выход системы (1)),
-ым ТМ (измеряемый скалярный выход системы (1)), ![]() ;
;![]() – постоянная
параметрически неопределенная матрица Якоби размерности
– постоянная
параметрически неопределенная матрица Якоби размерности ![]() ;
;![]() – постоянный вектор
настраиваемых параметров НБП размерности
– постоянный вектор
настраиваемых параметров НБП размерности ![]() ;
;![]() – вектор-столбец задаваемых параметров наблюдения (регрессии)
размерности
– вектор-столбец задаваемых параметров наблюдения (регрессии)
размерности ![]() ;
;![]() – скалярный
параметрический регулятор;
– скалярный
параметрический регулятор; ![]() – скалярная функция
активации (ФА) однослойного персептрона, получаемая нелинейным преобразованием
– скалярная функция
активации (ФА) однослойного персептрона, получаемая нелинейным преобразованием ![]() -ого управления
-ого управления ![]() и
и ![]() -ого наблюдения
-ого наблюдения ![]() .
.![]() -ый ТМ, представлена на Рисунке 1.
-ый ТМ, представлена на Рисунке 1.
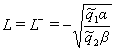
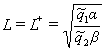
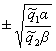 в первом и третьем квадранте Рисунка 2.
в первом и третьем квадранте Рисунка 2.