5. Технические науки

Іванов В. І., Скачков В. О., Мосейко Ю. В., Єгоров Ю. П.

Запорізька державна інженерна академія

ТЕРМОДИНАМІЧНІ ОСНОВИ МАТЕМАТИЧНОЇ МОДЕЛІ ДИФУЗІЙНОГО ПЕРЕНЕСЕННЯ МАСИ РЕЧОВИНИ

Розглядають відкриту термодинамічну систему, яка обмінюється із довкіллям масою речовини. Такий процесу обмежують відсутністю конвективної складової процесу перенесення маси у системі. При цьому об’єм системи під час дифузійного перенесення маси не змінюється, а змінюванням ентальпії у системі як результат змінювання концентрації маси можна нехтувати.

У такому разі рівняння другого закону термодинаміки набуває вигляду:

, (1)

де – хімічний потенціал -го компонента.

Процес, що розглядають, обмежують перенесенням одного компонента за .

Тоді із рівняння (1) одержують

. (2)

Маючи на указі, що , можна записати

, (3)

де – питомий потік маси.

Використовуючи відоме співвідношення із векторного аналізу, мають

, (4)

У рівнянні (4) виділяють дисипативний член, який відображує кількісну міру безповоротності процесу:

. (5)

З теореми про виробництво ентропії

, (6)

де – швидкість виробництва ентропії усередині системи за рахунок дисипативних ефектів безповоротних процесів перенесення маси речовини; – питомий потік дифузійного перенесення маси речовини, що спричинено дією сили ; – термодинамічна рушійна сила дифузійного перенесення маси речовини – визначають

, (7)

Враховуючи, що

, (8)

за одержують

. (9)

На підставі феноменологічного принципу лінійності потік маси речовини у системі подають співвідношенням

. (10)

де – кінетичний коефіцієнт перенесення маси речовини, , – коефіцієнт дифузії.

Таким чином, диференційне рівняння масопровідности за дифузійним перенесенням одного компонента у системі має вигляд:

. (11)

Під час розгляду двокомпонентної системи потенціал перенесення маси одного із компонентів визначають різницею хімічних потенціалів перенесення , тобто відносною величиною енергії, що необхідно для перенесення маси одного компонента до просторової області, яка зайнята іншим компонентом, котрий має свій хімічний потенціал.

У зв’язку з цим до формули (5) вносять відповідні змінювання:

. (12)

Оскільки згідно з рівнянням Гіббса-Дюгена за і

, (13)

де , – відносні концентрації першого та другого компонентів у системі з середньою щільністю , – за наявності однієї хімічної реакції градієнт потенціалу перенесення маси дорівнює:

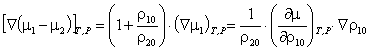. (14)

Маючи це на увазі, одержують

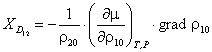. (15)

Тоді

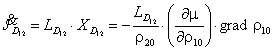. (16)

Вводять позначення 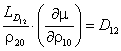та записують

, (17)

Тоді рівняння масопровідности під час дифузії першого компонента до просторової області, яка зайнята другим компонентом, набуває вигляду:

. (18)