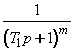СТРУКТУРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПРОЦЕССОВ ПРИГОТОВЛЕНИЯ ВОДОУГОЛЬНОГО ТОПЛИВА

 

Бондарь Татьяна Анатольевна

Восточноукраинский национальный

 университет им. Владимира Даля

Ключевые слова: Водоугольное топливо, диффузионная модель, плотность мелющих тел, измельчение, кинетика измельчения, матричная модель измельчения, движение потока.

 

Ввиду сложности процессов приготовления водоугольного топлива, проявляющейся в большом количестве информации, содержащейся в таких системах, и во взаимном влиянии параметров системы друг на друга, математические модели таких процессов удобно составлять по отдельным участкам, что значительно облегчает их реализацию на ЭВМ. Такой подход называется статической декомпозицией системы, при котором сложная система разбивается на ряд простых устройств, для каждого из которых составляются уравнения, связывающие входные и выходные параметры. В каждом конкретном случае полную модель процесса получают, комбинируя варианты отдельных участков. В зависимости от вида функции распределения все многообразие математических моделей потоков, возникающих в системах вентиляции и воздушного отопления, может быть представлено в виде некоторых типовых моделей, описанных ниже.

Модель идеального вытеснения. В соответствии с этой моделью, описывающей в первом приближении процесс в получения ВУТ, принимается поршневое течение потоков без перемешивания вдоль шаровой мельницы при равномерном распределении вязкости в направлении, перпендикулярном движению (табл. 1). Время пребывания в системе всех частиц одинаково и равно отношению объема системы к объемному расходу смеси.

Математическое описание модели имеет вид:

                                                                                                                              (1)

где: w- линейная скорость потока;

С – исследуемый параметр (в данном случае – кинематическая или динамическая вязкость водоугольного топлива);

τ – время;

x-  продольная координата.

 

Модель идеального перемешивания. Согласно этой модели принимается равномерное распределение  исследуемого параметра температуры во всем потоке.

Зависимость между вязкостью ВУТ на входе νвх и выходе ν вых имеет вид:

 

                                                             (2)

Функция отклика системы:

 

где: - - среднее время пребывания ВУТ в системе.

Модели идеального перемешивания следуют процессы, в условиях интенсивного перемешивания.

Диффузионная модель. Различают однопараметрическую и двухпараметрическую диффузионную модель.

Однопараметрическая диффузионная модель. В данном случае основой является модель вытеснения, осложненная обратным перемешиванием, следующим формальному закону диффузии. Параметром, характеризующим модель, служит коэффициент турбулентной диффузии или коэффициент продольного перемешивания DL. При составлении однопараметрической диффузионной модели принимаются следующие допущения:

- изменение вязкости ВУТ является непрерывной функцией координаты (расстояния);

- вязкость в данном сечении постоянна;

- объемная скорость потока и коэффициент продольного перемешивания не изменяются по длине и сечению потока.

При таких допущениях модель описывается уравнением:

                                                                            (3)

Уравнение (3) отличается от уравнения (2) введением дополнительного члена  учитывающего, турбулентную, диффузию или перемешивание. Величина определяется опытным путем.

Двух параметрическая диффузионная модель. В этой модели учитывается перемешивание потока в продольном и радиальном направлениях, причем модель характеризуется коэффициентами продольного DL и радиального DZ перемешивания. При этом принимается, что величины DL и DZ не изменяются по длине и сечению шаровой мельницы, а скорость постоянна.

При условии движения потока в водоугольной смеси с постоянной по длине и сечению скоростью уравнение двухпараметрической модели имеет вид:

                                                                             (4)

При опытном определении коэффициентов продольного и радиального перемешивания DL и DZ их обычно представля­ют в виде безразмерных комплексов - критериев Пекле , где L - определяющий линейный размер шаровой мельницы.

В этом случае уравнение диффузионной модели также приводится к безразмерному виду. С этой целью вводится безразмерная вязкость — безразмерная длина  и время , где V — объем мельницы; Vt — производительность системы.

Учитывая, что производительность мельницы принимается постоянной, уравнение (4) приводится к виду:

                                                                                                                                          (5)

Если , диффузионная модель переходит в модель идеального вытеснения; если , диффузионная модель переходит в модель идеального смешения. Для малых отклонений от потока идеального связь между дисперсией σ2 и  дается в виде уравнения:

,                                                                                   (6)

 

Зависимость коэффициента продольного перемешивания DL различных факторов (размера мельницы, скорости по­тока, физических свойств ВУТ и т. д.) устанавливается опытным путем при постановке опытов с использованием теории подобия.

Ниже приведены значения коэффициента продольного перемешивания, полученные для различных случаев.

Для однофазного потока в ламинарной области:

                                                                       (7)

В этом выражении:

 - критерий Шмидта;

 - критерий Рейнольдса;

DL - коэффициент молекулярной диффузии.

 

В турбулентной области молекулярной диффузией пренебрегают:

                                                                                                           (8)

где - коэффициент трения (для течения в трубопроводе) или параметр, характеризующий конфигурацию стенок, вдоль которых распространяется поток.

Для переходной области предложено эмпирическое уравнение:

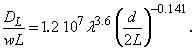                                                                                          (9)

Ячеечная модель. Основой модели является представление об идеальном перемешивании в пределах слоев, расположенных последовательно, и отсутствии перемешивания между ними. Параметром, характеризующим модель, служит число ячеек m.

Математическое описание ячеечной модели включает m линейных дифференциальных уравнений первого порядка

 

                                                                                                                  (10)

где: i =1, 2, . . ., m .

Связь между распределением по ν - кривой и числом ячеек m определяется из соотношения:

                                                                                                                 (11)

где:

Соотношение между числом ячеек и дисперсией σ2 дается виде: '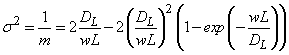                                                 (12)

или с достаточной для практических расчетов точностью при m > 10:

                                                                                                                                      (13)

При m = 1 ячеечная модель переходит в модель идеального смешения, а при  - в модель идеального вытеснения. Ячеечной модели соответствуют последовательно соединенные помещения с интенсивным перемешиванием или наличие различных зон в помещении.

Комбинированные модели. Не все реальные процессы удается описать с помощью рассмотренных выше моделей, в частности включающих циркуляционные потоки, а также процессы при наличии застойных зон. В таких случаях используются  комбинированные модели.

При построении комбинированной модели принимают, что рабочий объем мельницы из отдельных зон, соединенных последовательно или параллельно, в которых наблюдаются различные структуры потоков: зона поршневого потока (идеального вытеснения), зона потока с идеальным перемешиванием; зона с продольным  перемешиванием; зона застойная.

Помимо этого, могут наблюдаться следующие локальные потоки: байпасный, циркуляционный, проскальзывание и т. д.

Наличие указанных видов потоков устанавливается по опытным кривым зависимости выходной величины от входной. Следует иметь в виду, что увеличением количества зон можно описать процесс любой сложности, но математическое моде­лирование одновременно усложняется.

В таблице 1 приведены передаточные функции типовых идеальных моделей.

Таким образом, предложена классификация и математические модели для различных условий работы шаровых мельниц, критериальные выражения и передаточные функции процессов.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таблица 2

Передаточные функции типовых моделей

 

Тип модели

Передаточная функция

Примечание

Идеальное смешение

V- объем помещение;

Vt - производительность вентилятора

Идеальное вытеснение

exp(-pT)

T=L/w - транспортное запаздывание в помещении;

w – линейная скорость газа

m слоев в ряд идеального смешения равного объема

 

m слоев в ряд идеального смешения неравного объема

. . .

. . .

Идеальное вытеснение и смешение

 

 

Литература.

1.                 Б.Ф.Брагин, А.С.Коломиец Пульпы и суспензии (технологии, оборудование, расчёты)- К.:- ИС и О.- 1995.-464с.

2.                 А.С.Кондратьев, В.М.Овсянников, Е.П.Олофинский и др. Транспортирование водоугольных суспензий , гидродинамика и температурный режим. -М.:- Недра.- 1988.-213с.

3.                 Урьев Н.Б., Потанин А.А. Текучесть суспензий и порошков. –М.:- Химия, 1992 - 256 с.

4.                 Исследование гидромеханики суспензий в трубопроводном транспорте. Сборник научных трудов. – М.:-  ВНИИПИгидротрубопровод. – 1985. – 103с

5.                 Физико-химические основы регулирования структурно-реологических свойств и устойчивости, высококонцентрированных водоугольных суспензий в процессе трубопроводного гидротранспорта. Сборник научных трудов. – М.: - НПО «Гидротрубопровод». – 1989. -124 с.

6.                 Е.Е.Серго. Дробление, измельчение и грохочение полезных ископаемых. - М.: - Недра.-1985.-285с.

7.                 Г.С. Ходаков Физика измельчения. Монография. - М.- Наука. - 1972 -307 с.