Аспирант Калимулин И.Ф., к.т.н. Заболоцкий А.М.

Томский государственный университет систем управления
и радиоэлектроники

Методика получения широкополосной модели конденсатора

Для обеспечения электромагнитной совместимости (ЭМС) электронных блоков космических аппаратов (КА) выполняются комплексные испытания, которые описаны стандартами MIL-STD-461F и AIAA S-121-2009. Однако, такие испытания занимают много времени, являются дорогостоящими, и часто КА не проходит их с первого раза. Кроме этого, если в результате измерений было установлено, что параметры КА выходят за установленные рамки одного из пунктов стандарта, то разработчикам далеко не всегда очевидно, какие изменения необходимо внести в электрическую схему и в конструкцию печатной платы, чтобы повторные испытания на ЭМС прошли успешно [1].

Одним из решением данной проблемы является использование компьютерного моделирования как на ранних этапах проектирования электрической схемы и конструкции печатной платы, так и по завершению разработки бортовой аппаратуры КА. Однако, для выполнения компьютерного моделирования необходимы широкополосные математические модели электронных компонентов, описывающие их поведение не только в рабочем диапазоне частот, но и до 40 ГГц.

Данные математические модели получают из S-параметров, используя следующие подходы: аппроксимация рациональными функциями и синтез цепей [2, 3]; аналитический подход на основе конструкции [4, 5]; структурно-параметрическая оптимизация [6, 7]. Оптимизация и аналитический подход обычно совмещаются, чтобы получить модель за приемлемое время, однако поточное создание для разнородных компонентов требует большого количества ручной работы. В [2, 3] приведены примеры создания моделей корпуса компонента и внутрикристальной индуктивности. Однако, в приведённых работах не представлена в явном виде методика получения моделей для конденсаторов.

Цель работы – представить методику для получения широкополосных моделей конденсатора, используя аппроксимацию рациональной функцией.

Предлагаемая методика состоит из следующих этапов: 1) измерение коэффициента отражения S₁₁ компонента; 2) пересчёт S₁₁ в импеданс Z; 3) аппроксимация импеданса Z рациональной функцией методом vector fitting; 5) реализация элементарных дробей эквивалентными схемами, используя методы синтеза цепей; 6) формирование итоговой SPICE-модели; 7) верификация модели.

Рассмотрим процесс получение широкополосной модели конденсатора К10‑17а‑0.47 ±5% мкФ по предложенной методике. Измерение коэффициента отражения S₁₁ выполнено на векторном анализаторе цепей. Для выполнения измерений конденсатор напаивался на коаксиально-микрополосковый переход типа SMA.

После пересчёта S₁₁ в Z выполнена аппроксимация рациональной функцией методом vector fitting [8–10]. В результате получаем рациональную функцию:

,

(1)

где N – порядок аппроксимации, его выбор зависит от сложности функции S₁₁ и желаемой точности получаемой модели. Но при слишком большом порядке аппроксимации размер модели будет слишком большим, что увеличит время её расчёта. Для указанного конденсатора достаточно N=6. Первый член функции раскладывается на сумму дробей с комплексно-сопряжёнными полюсами вида:

(2)

Каждая такая сумма (2) реализовывается в виде параллельного контура _pi (R1_pi, R2_pi, L_pi, C_pi) (рис. 1). Для расчёта параметров контура воспользуемся формулами [11]. В результате, итоговая эквивалентная схема конденсатора будет состоять из 6 последовательно соединённых контуров.

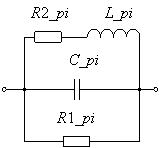
Рисунок 1 – Схема параллельного контура

Для верификации модели выполнено её схемотехническое моделирование в системе TALGAT [12]. Частотная зависимость импеданса Z, вычисленного по полученной модели, приведена на рис. 2. Модуль разности между измеренными и вычисленными результатами, представлен на рис. 3.

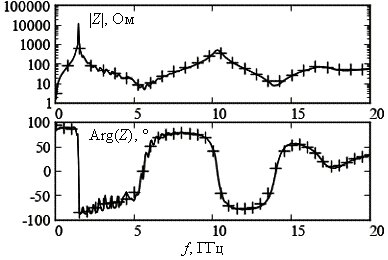
Рисунок 2 – Импеданс конденсатора: измерения (–), модель (+)

Рисунок 3 – Верификация модели конденсатора: модуль разности между результатами измерений и моделирования

Среднеквадратичное отклонение (RMS) составляет 5,25. Таким образом, можно сделать вывод, что полученная модель конденсатора является точной и ее можно использования при выполнении анализа ЭМС печатных плат.

Предложенная методика позволяет получать модели для конденсаторов, состоящие из RLC-элементов. На основе её получена широкополосная SPICE-модель резистора К10‑17а‑0.47 ±5% мкФ в виде эквивалентной схемы, с рабочим диапазоном до 20 ГГц. В дальнейшем планируется доработать методику получения широкополосных моделей для любых пассивных электронных компонентов.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 13-07-98017 р_сибирь_а.

Литература

1. Кечиев Л.Н., Васильевич Л.Н. Виртуальная сертификация радиоэлектронных средств по уровню помехоэмиссии как средство подготовки к лабораторным испытаниям по электромагнитной совместимости // Труды научно-исследовательского института радио. 2010. № 1. С. 57–70.

2. Kim Y.-J., Kwon O.-K., Lee C.-H. Equivalent circuit extraction from the measured S-parameters of electronic packages // ICVC’99. 6th International Conference on VLSI and CAD (Cat. No.99EX361). IEEE, 1999. P. 415–418.

3. Liang Y., Wang Y., Li L. Rational modeling of on-chip inductor by vector fitting // Analog Integrated Circuits and Signal Processing. 2010. Vol. 65. № 2 P. 253–258.

4. Kim M.-G., Lee B.H., Yun T.-Y. Equivalent-Circuit Model for High-Capacitance MLCC Based on Transmission-Line Theory // IEEE Transactions on Components, Packaging and Manufacturing Technology. 2012. Vol. 2. № 6. P. 1012–1020.

5. Калимулин И.Ф., Газизов Т.Р., Заболоцкий А.М. Импеданс низкочастотных пассивных компонентов бортовой аппаратуры в диапазоне до 20 ГГц // Приборы и техника эксперимента. 2012. № 2. P. 91–97.

6. Rahimi Pordanjani I. и др. A Method to Construct Equivalent Circuit Model From Frequency Responses With Guaranteed Passivity // IEEE Transactions on Power Delivery. 2011. Vol. 26. № 1. P. 400–409.

7. Калимулин И.Ф., Мелкозёров А.О. Оптимизация параметров математической модели резистора по критерию соответствия расчетного модуля коэффициента отражения измеренному в диапазоне до 20 ГГц // Доклады Томского государственного университета систем управления и радиоэлектроники. 2012. № 2(26). С. 66–70.

8. Gustavsen B., Semlyen A. Rational approximation of frequency domain responses by vector fitting // IEEE Transactions on Power Delivery. 1999. Vol. 14. № 3. P. 1052–1061.

9. Gustavsen B. Improving the pole relocating properties of vector fitting // Power Delivery, IEEE Transactions on. 2006. Vol. 21. № 3. P. 1587–1592.

10. Deschrijver D., Mrozowski M. Macromodeling of multiport systems using a fast implementation of the vector fitting method // Microwave and Wireless Components Letters, IEEE. 2008. Vol. 18. № 6. P. 383–385.

11. Balabanian N. Network Synthesis. Englewood Cliffs: Prentice-Hall, 1958.

12. Официальный сайт TALGAT System [Электронный ресурс]. – Режим доступа: http://talgat.org/, свободный (дата обращения 26.11.2013)