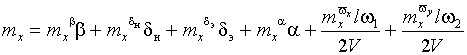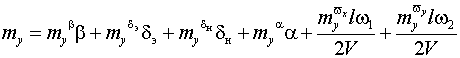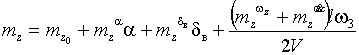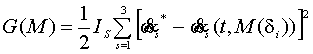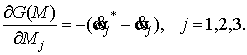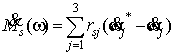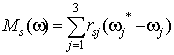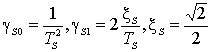Технические науки./9 Авиация и космонавтика.

Д.т.н. Сизых В.Н.

Иркутский Государственный университет путей сообщения. Россия

Диль В.Ф.

Иркутский филиал Московского Государственного технического университета гражданской авиации. Россия

МЕТОДИКА СИНТЕЗА АЛГОРИТМОВ УПРАВЛЕНИЯ ВРАЩАТЕЛЬНЫМ ДВИЖЕНИЕМ ЛЕТАТЕЛЬНОГО АППАРАТА НА ОСНОВЕ ПРИНЦИПА СИММЕТРИИ И КОНЦЕПЦИИ ОБРАТНЫХ ЗАДАЧ ДИНАМИКИ

Синтез законов управления ЛА нелинейной модели может быть практически реализован при опоре на ряд принципов: принцип инвариантности (сохранения энергии) диссипативных систем, принцип минимального вмешательства в процессы управления этими системами, принцип симметрии.

В основу теории, реализующей принцип симметрии движения, может быть положена одна из концепций обратных задач динамики (ОЗД), разработанная П.Д. Крутько: использование для нелинейных систем методов ОЗД в сочетании с минимизацией локальных функционалов энергии движения.

Решение обратной задачи динамики сводится к нахождению таких управляющих силы и моментов, под действием которых движение объекта осуществлялось бы по назначенной траектории.

При этом формирование нелинейных законов управления может быть равнозначно осуществлено по силовым или моментным характеристикам модели пространственного движения ЛА.

Сформулируем задачу синтеза нелинейной системы управления вращательным движением неманевренного ЛА методом обратных задач динамики. При этом осуществляется оптимизация управления вращательным движением по локальным функционалам, характеризующим энергию движения [5].

Основной математической модели (ММ) является модель ЛА, как абсолютно твердого тела, пространственное движение которого описано в инерциальной системе координат нелинейной дифференциальной системой уравнений [1]

, (1)

где х – n-мерный вектор фазовых координат; u – m-мерный вектор управляющих воздействий; – n-мерная векторная функция указанных аргументов.

Вращательное движение ЛА в связанной системе координат (СК) описывается динамическими уравнениями Эйлера [1], имеет вид

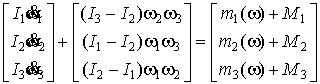, (2)

где , M_s – управляющий момент; m_s(ω) – суммарные моменты, характеризующие изменение кинетической энергии вращающихся частей авиадвигателя и влияние диссипативных сил, s =1..3.

Управляющий момент зависит от аэродинамической компоновки ЛА и положения органов управления.

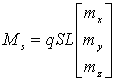, (3)

Где – диагональная матрица характеристических линейных размеров ЛА, m_i -безразмерные коэффициенты аэродинамических моментов, действующих вокруг осей связанной СК). Они выражаются следующим образом [1]:

,
,	(4)
,

где S – эффективная площадь крыла, – скоростной напор, V – воздушная скорость,

Алгоритмы управления вращательным движением ЛА наиболее просто синтезируются методом обратных задач динамики в сочетании с оптимизацией системы (2) по локальным функционалам, характеризующим энергию движения [5].

Основные этапы методики синтеза алгоритмов управления вращательным движением ЛА сводятся к следующему:

1. Динамические характеристики проектируемой системы назначаются с помощью эталонных моделей для каждой степени свободы по реакции на «скачок» рулей. Назначенные траектории определяют требуемый пространственный манёвр ЛА и характеризуются свойствами эталонных моделей вращательного движения.

2. Структура алгоритмов и их параметры выбираются из условия отслеживания с необходимой точностью фазовых траекторий эталонных моделей вращательного движения.

3. Степень близости угловых скоростей объекта и эталона оценивается с помощью квадратичных функционалов энергии ускорения. Процесс движения к экстремуму – минимуму организуются по схеме градиентного метода.

Утверждается [5], что такие алгоритмы управления обладают свойствами естественной адаптивности, позволяют осуществить декомпозицию нелинейной системы (2) по степеням свободы за счёт организации обратных связей с большими, но ограниченными коэффициентами усиления.

Применительно к задаче управления вращательным движением ЛА в статье предлагается алгоритм синтеза управления по ускорениям.

Сформулируем задачу синтеза управлений на примере стабилизации угловых скоростей на интервале времени , полагая t₀=0, момент времени нефиксированной величиной.

Пусть в текущий момент времени состояние управляемого объекта характеризуется значениями угловых скоростей

Требуется найти такие управляющие воздействия δ_i , при которых система (2) переходит из исходного состояния в новое состояние и находится в этом состоянии бесконечно долго. При этом необходимо, чтобы угловые скорости управляемого движения с требуемой точностью следовали за угловыми скоростями, определяемыми эталонной моделью:

,

(5)

где , установившееся движение устойчиво: при t→∞.

Степень приближения управляемого процесса к эталонной модели оценивается функционалом

,

(6)

который характеризует энергию ускорения вращательного движения в окрестности фазовых траекторий эталонной модели.

Наиболее просто сформулированная задача синтеза решается, если в качестве управляющих функций выбирать не отклонения рулей ЛА, а управляющие моменты . Тогда на первом этапе синтезируются законы управления моментами, а затем из формул (3), (4) через решение системы алгебраических уравнений будут определены искомые управляющие воздействия .

Законы управления по каждой степени свободы получаем, применяя схему простого градиентного метода

.

(7)

Компоненты градиента определяются из уравнения (2) и равны

Отсюда следует, что

,

или после интегрирования по времени обеих частей, получим:

,

(8)

где требуемые значения угловой скорости вычисляются из (5), структура матрицы определяется характером перекрестных связей по в (4)

.

Если R=R^Т>0 , то Ġ(M)<0 и замкнутая регулятором система (2) асимптотически устойчива по Ляпунову [5]: при t→∞.

Управляющие воздействия δ_i определяются из уравнений (3), (4), (8)

Углы атаки и скольжения определяются из кинематических соотношений поступательного движения ЛА (из траекторного контура управления) и характеризуют связь силовых и моментных характеристик ЛА в связанной СК. Для пилотажного контура величины углов α, β являются задающими воздействиями.

Структурная схема контура управления представлена на рисунке 1.

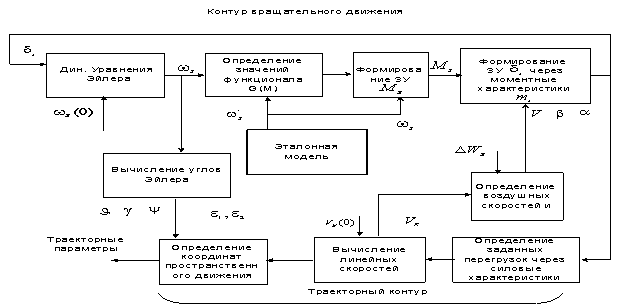
Рис. 1. – Структурная схема контура управления

В процессе исследования контура управления вращательным движением с подстройкой под эталонную модель, рассчитывались параметры эталонной модели (5) по формулам (9), в которых постоянные времени определялись путем имитационного моделирования на языке Паскаль по реакции нелинейной модели самолёта ИЛ-76М на "скачки" рулей высоты, направления и элеронов в 10 градусов.

(9)

Достоверность полученных результатов моделирования проверялась путём варьирования коэффициентов усиления в законах управления вращательным движением ЛА при решении задачи стабилизации угловых скоростей.

Проведенные исследования показали справедливость разработанных ранее теоретических положений: чем больше значения коэффициентов усиления в законах управления, тем выше близость угловых скоростей вращательного движения к угловым скоростям эталонной модели

( при ).

Результаты моделирования на алгоритмическом языке MathCAD для случая средних значений коэффициентов усиления представлены соответственно на Рисунках 2–4.

t,c

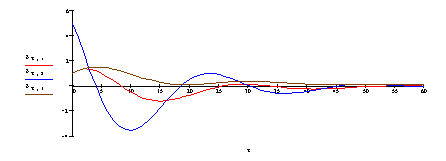
Рис. 2. – Отклонения рулей

t,c

М, Н*m

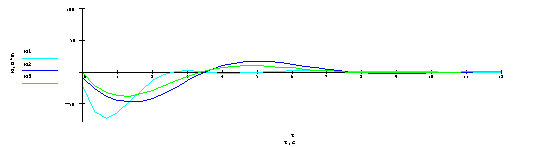
Рис. 3. – Изменение управляющих моментов

t,c

w, рад/с

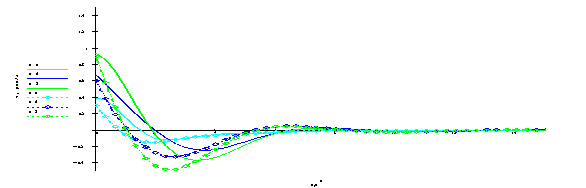
Рис. 4. – Подстройка угловых скоростей под эталон

Сравнительный анализ результатов моделирования показывает, что отработка рассогласования угловых скоростей вращательного движения ЛА в нелинейной САУ происходит за более короткое время и с меньшими амплитудами параметров, то есть интенсивнее, чем при использовании штатных законов управления САУ-1Т-2Б самолета среднего класса Ил-76. Эффективность управления при этом проявляется в более высоком качестве переходных процессов по высоте и по отклонению руля высоты.

Важно также отметить, что технологии решения обратных задач динамики являются основой для построения интегрированных систем управления мехатронных и робототехнических систем [6].

Литература

1. Красовский А.А. Системы автоматического управления полетом и их аналитическое конструирование. / А.А. Красовский. – М.: Наука, 1973. – 373 с.

2. Буков В.Н., Сизых В.Н. Метод и алгоритмы решения сингулярно-вырожденных задач аналитического конструирования регуляторов / В.Н. Буков, В.Н. Сизых // Изв. АН. Теория и системы управления. 2001, №5. – 43-61.

3. Пятницкий Е.С. Синтез иерархических систем управления механическими и электромеханическими объектами на принципе декомпозиции / Е.С. Пятницкий // Автоматика и телемеханика. 1989, № 1. – С. 14-32.

4. Машиностроение. Энциклопедия. Том I-4. Автоматическое управление. Теория. М.: Машиностроение, 2000. – 792 с.

5. Крутько П.Д. Обратные задачи динамики в теории автоматического управления. / П.Д. Крутько. – М.: Машиностроение, 2004. – 573 с.

6. Мехатроника: компоненты, методы, примеры. / Б. Хайманн, В. Герт, К. Попп, О. Репецкий/ Под ред. О.В. Репецкого. – Новосибирск: Изд-во СО РАН, 2010. – 602 с.