Математика/ 4

А.С. Кушкумбаева

«Магнитогорский государственный технический университет

им. Г. И. Носова» (ФГБОУ ВПО «МГТУ»), Россия

Визуализация решений первой краевой задачи для

консервативного автономного уравнения Дуффинга

с использованием методов теории ветвления

Для описания физических процессов в теории колебаний применяются математические модели. Осциллятор Дуффинга или осциллятор с кубической нелинейностью является одной из наиболее распространенных моделей теории колебаний. Осциллятор Дуффинга (англ. Duffingoscillator) — простейшая одномерная нелинейная система. Особенностью осциллятора Дуффинга является возможность получения хаотической динамики.

Уравнение осциллятора имеет вид:

Рассмотрим модель, описывающую консервативный автономный осциллятор Дуффинга, называемый также идеальным осциллятором:

Произведя замену переменных и выбрав следующие значения параметров: (где - малый параметр), будем рассматривать первую краевую задачу для уравнения Дуффинга:

(1)

(2)

которая получается из краевой задачи, с помощью фиксирования краевых условий:

В целях данной статьи были исследованы решения краевой задачи (1)-(2), в результате чего была получена зависимость числа различных решений от параметра , приведенная в таблице 1.

Таблица 1. Зависимость числа приближенных решений от параметра где

Число различных решений	0	3	2	5	4	7	6
	[0,)

Приведем графики найденных приближенных аналитических решений краевой задачи (1)-(2) при выбранных значениях:

1. методами нахождения решения в виде ряда с коэффициентами до 4-го порядка.

2. методами стрельбы.

Метод стрельбы (краевая задача) — численный метод, заключающийся в сведении краевой задачи к некоторой задаче Коши для той же системы дифференциальных уравнений.

3. методами квазилинеаризации с шагом h= 0,001 и точностью toch= 0,01.

Квазилинеаризация - совокупность приемов численного решения нелинейных задач путем сведения их к последовательности линейных задач. В основе аппарата квазилинеаризации лежит метод Ньютона и его обобщение на функциональные пространства, теория дифференциальных неравенств и метод динамическое программирования. Наиболее простым примером, иллюстрирующим приемы К., является использование метода Ньютона - Рафсона для отыскания корня r скалярной монотонно убывающей строго выпуклой функции . В этом случае на каждом шаге итеративного процесса исходная нелинейная функция аппроксимируется линейной , отыскивается корень , который служит следующим приближением, так что

Построенная последовательность обладает свойством монотонности ( х 0<х 1<х 2<...<r) и квадратичной сходимости Применение К. для решения уравнения Риккати (предполагается, что решение существует на отрезке [0, t0]) выглядит следующим образом.

Исходное уравнение заменяется эквивалентным

где минимум берется по функциям , заданным на . Данное уравнение обладает рядом свойств, присущих линейным уравнениям, и для его решения используется линейное дифференциальное уравнение

где - некоторая фиксированная функция. Опираясь на свойство (причем равенство имеет место при ), можно построить систему последовательных приближений

удовлетворяющих линейным уравнениямТо же самое рекуррентное соотношение может быть получено путем применения метода Ньютона - Канторовича к исходному нелинейному уравнению.

Использование схемы К. при решении краевой задачи для нелинейных дифференциальных уравнений второго порядка

приводит к следующей последовательности функций , удовлетворяющих линейным уравнениям

с линеаризованными краевыми условиями

Существование, единственность и квадратичная сходимость последовательности следуют из соответствующей выпуклости функций при достаточно малом интервале .

Метод К. находит применение при решении двухточечных и многоточечных краевых задач для линейных и нелинейных обыкновенных дифференциальных уравнений, краевых задач для эллиптических и параболических уравнений в частных производных, вариационных задач, дифференциально-разностных и функционально-дифференциальных уравнений и т. д. Как и всякая итеративная схема, метод К. удобен для реализации на ЭВМ, допускает различные модификации, позволяющие ускорить сходимость для более узких классов задач. Существуют разнообразные примеры его использования как эвристического способа решения ряда физических, технических и экономических задач.

1. При получаем 3 решения (см. таблицу 1):

(3)

(4)

Замечание. Знаки «+/-» для решений (3) для выбираются верхние, для - нижние. Для других подобных случаев знаки выбираются тем же образом.

Визуализация приближенных решений выбранными методами при заданном имеет вид, указанный на рисунке 1.

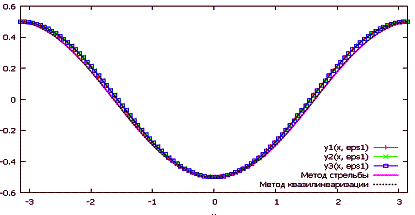
Рис. 1. Визуализация приближенных решений задачи (1)-(2) при выбранном методом нахождения решения в виде ряда (решения (3)-(4)); методами стрельбы и квазилинеаризации с шагом h= 0,001 и точностью toch= 0,01.

2. При получаем 5 решений:

(5)

(6)

(7)

Визуализация приближенных решений выбранными методами при заданном имеет вид, указанный на рисунке 2.

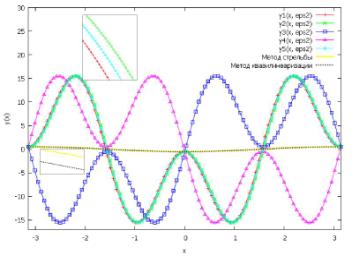
$C:\Users\C3E0~1\AppData\Local\Temp\FineReader11.00\media\image1.jpeg$

Рис. 2. Визуализация приближенных решений задачи (1)-(2) при выбранном методом нахождения решения в виде ряда (решения (5)-(7)); методами стрельбы и квазилинеаризации с шагом h= 0,001 и точностью toch= 0,01.

3. При получаем 7 решений:

(8)

(9)

(10)

(11)

Визуализация приближенных решений выбранными методами при заданном имеет вид, указанный на рисунке 3.

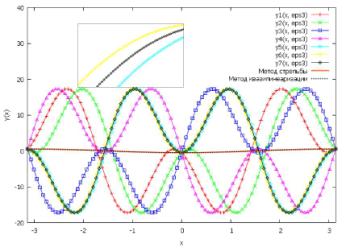
$C:\Users\C3E0~1\AppData\Local\Temp\FineReader11.00\media\image2.jpeg$

Рис. 3. Визуализация приближенных решений задачи (1)-(2) при выбранном методом нахождения решения в виде ряда (решения (8)-(11)); методами стрельбы и квазилинеаризации с шагом h= 0,001 и точностью toch= 0,01.

В целях данной статьи были исследованы графики полученных приближенных решений, и было установлено, что при , близких к , приближенное аналитическое решение методом разложения в ряд (при коэффициентах до 4-го порядка) будет близко к численным решениям, полученным методами стрельбы и квазилинеаризации. При,приближающихся к и более, видно, что выбранного числа членов ряда явно недостаточно для корректного приближения аналитического решения. Это также видно на рисунках 1-3 при выбранных , , .

Литература:

1. Дубровский В.В., Торшина О.А. Проблема решения задач на собственные значения для дифференциальных операторов со сложным вхождением спектрального параметра // Новые мат. методы. Электромагн. волны и электронные системы. 2002. №9. Т.7. С. 4-10.

2. Торшина О.А. Алгоритм вычисления регуляризованного следа оператора Лапласа – Бельтрами с потенциалом на проективной плоскости // Вестник МаГУ. Математика. 2003. В. 4. С. 183-215.

3. Торшина О.А. Следы дискретных операторов с частными производными // Альманах современной науки и образования. Научно-теоретический/ тематический журнал. Тамбов: Грамота, № 4 (59), 2012. С.238. С. 220-222.

4. Дубровский В.В., Торшина О.А. Формула первого регуляризованного следа для дифференциального оператора Лапласа – Бельтрами // Дифференциальные уравнения и их приложения. 2002. №1. С. 9-19.

5. Торшина О.А. Численный метод вычисления поправок теории возмущений // Альманах современной науки и образования. Научно-теоретический/ тематический журнал. Тамбов: Грамота, № 12, 2013. С. 168-170.