Сатыбалдиев О.С., Сахабаева
А.М.
Қ.И.Сәтбаев
атындағы ҚазҰЗТУ, Қазақстан
Экспоненциалдық
өсу заңдылықтарының математикалық формулалары
Популяция
санының өсуінің негізгі заңдылығын айқындау
үшін қарапайым мысалға жүгінелік. Айталық,
қандайда бір клеткалы организм қарапайым бөліну жолы
арқылы көбейсін және әрбір сағатта бөліну
процесі жүріп отырсын. Мұндай жағдайда бөліну
нәтижесіне сәйкес 4 сағат өткеннен кейін оның
саны 2; 8 сағаттан кейін 4; 12 сағаттан кейін 8; 16 сағаттан
кейін 16; 20 сағаттан кейін 32; 24 сағаттан кейін 64; 28
сағаттан кейін 128; 32 сағаттан кейін 256 және т.б.
|
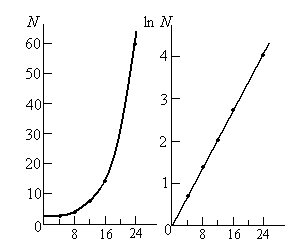
1-сурет. Әрбір төрт сағатта бөлінетін бір клеткалы
организмнің экспоненциалдық өсуі: а) Арифметикалық
шкала, б) Логарифмдік шкала |
Бұл
өсудің графигі 1,а-суретінде
кескінделген. Бұл экспоненциалдық заңдылықпен
кескінделген қисық деп аталады. Оған сәйкес келетін
теңдеу ![]() түрінде
жазылады. Мұндағы
түрінде
жазылады. Мұндағы ![]() мезгіліндегі
популяцияның саны;
мезгіліндегі
популяцияның саны; ![]() бастапқы
бастапқы ![]() уақытындағы популяция саны;
уақытындағы популяция саны; ![]() - натурал логарифмнің негізі;
- натурал логарифмнің негізі; ![]() - осы популяция санының көбею
қарқынының сипаттау көрсеткіші. Қандайда бір
мезгіл аралығында популяция санының экспопненциалдық
түрдегі өсу қарқыны сақталынуы үшін бір
ғана шарт қажет. Ол шарт:
- осы популяция санының көбею
қарқынының сипаттау көрсеткіші. Қандайда бір
мезгіл аралығында популяция санының экспопненциалдық
түрдегі өсу қарқыны сақталынуы үшін бір
ғана шарт қажет. Ол шарт: ![]() көрсеткішінің тұрақтылығы. Популяция
өсуінің лездік салыстырмалы жылдамдығын
көрсеткішінің тұрақтылығы. Популяция
өсуінің лездік салыстырмалы жылдамдығын ![]() болады. Бұл
жазу формасы популяция санының өсу жылдамдығының
оның санына пропорционал екендігін көрсетеді. Популяция санын
логарифмдік масштаб жағдайда кескіндесек, онда өсудің
экспоненциалдық графигі (1,б-сурет)
түзу сызық болады. Өсудің экспоненциалдық түрінің логарифмдік
формасының теңдеуі
болады. Бұл
жазу формасы популяция санының өсу жылдамдығының
оның санына пропорционал екендігін көрсетеді. Популяция санын
логарифмдік масштаб жағдайда кескіндесек, онда өсудің
экспоненциалдық графигі (1,б-сурет)
түзу сызық болады. Өсудің экспоненциалдық түрінің логарифмдік
формасының теңдеуі ![]() болады, яғни ол
бұрыштың коэффициенті
болады, яғни ол
бұрыштың коэффициенті ![]() -ге тең түзудің теңдеуі.
-ге тең түзудің теңдеуі. ![]() коэффициенті сол
түзудің өспен жасайтын көлбеу бұрышын сипаттайды.
коэффициенті сол
түзудің өспен жасайтын көлбеу бұрышын сипаттайды.
Кезкелген
организмдер тобының экспоненциалдық заң бойынша өсу
процесі табиғи сұрыптау теориясын құрудың негізгі
алғы шарты. Дарвиннің өзі әртүрлі организмдер
популяциясының өсу мүмкіндіктерінің
қарқынды екенін есептеген. Оның зерттеулері бойынша
пілдің бір қосағынан таралған ұрпақ 750
жылдан кейін 19 миллионға жетеді екен. Егер өте тез көбейетін
организмдерді қарастырсақ, олардың саны фантастикалық
болады. Мысалы, қандайда бір организм өте қолайлы ортада
әрбір 20 минут сайын көбейіп отырса, онда ол организмнен
туындаған организмдер 36 сағаттан кейін бүкіл жер шарын
қалыңдығы 30см болатын қабатпен жабады екен. Одан
кейінгі 2 сағаттың ішінде бұл қабаттың
қалыңдығы 2 метрге жетеді екен.
Жер
шарын мұндай қалыңдықта жабатын бактериялар мен
миллиондаған пілдер жоқ. Олай болса мынандай тұжырымға
келеміз: табиғатта экпоненциалдық өсу бар болса, онда белгілі
бір уақыт өткеннен кейін олардың саны кемиді немесе
қалыпты бір деңгейге келеді. Табиғатта болмайтын мұндай
процесстерге назар аударудың қаншалықты қажеті бар
деген сауалдың туатыны табиғи нәрсе. Бұл сауалға
мынандай жауап бар: экспоненциалдық түрдегі модель, ең
алдымен, популяция өсуіндегі потенциалдық мүмкіндіктерді сипаттау
үшін пайдаланылады. Өзінің экспоненциалдық формасын
белгілі бір уақыт аралығында сақтайтын популяцияның
саны мен осы уақыт аралығында өмір сүруші популяция
санының айырымы арқылы өлу қарқынын табуға
болады.
Жыртқыш
және жемтік популяцияларының сандарының ауытқуын
кескіндейтін математикалық модельдерді құралық. Егер
жыртқыштар болмаған жағдайда жемтіктің саны
экспоненциалдық түрде өседі және жемтіктің
өлімі жыртқыш пен жемтіктің кездесу жиілігіне пропорционал
деп ұйғарсақ, онда популяция санының лездік өзгеру
жылдамдығы ![]() төменгі
теңдеу арқылы өрнектеледі:
төменгі
теңдеу арқылы өрнектеледі: ![]()
Мұндағы ![]() - жемтік популяциясының өсуінің
салыстырмалы лездік жылдамдығы,
- жемтік популяциясының өсуінің
салыстырмалы лездік жылдамдығы, ![]() - жемтіктің өлімі мен жыртқыш санының
орналасу тығыздығын байланыстыратын тұрақты шама,
- жемтіктің өлімі мен жыртқыш санының
орналасу тығыздығын байланыстыратын тұрақты шама, ![]() мен
мен ![]() сәйкес
жыртқыш пен жемтіктің орналасу тығыздықтары. Бұл
модель бойынша жыртқыш популяциясының өсуінің лездік
жылдамдығы
сәйкес
жыртқыш пен жемтіктің орналасу тығыздықтары. Бұл
модель бойынша жыртқыш популяциясының өсуінің лездік
жылдамдығы ![]() туу мен
тұрақты өлімнің айырмасына тең, яғни
туу мен
тұрақты өлімнің айырмасына тең, яғни ![]() .
.
Мұндағы ![]() - жыртқыш популяциясының тууы мен
құрбандықтың орналасу тығыздығын байланыстыратын
тұрақты шама, ал
- жыртқыш популяциясының тууы мен
құрбандықтың орналасу тығыздығын байланыстыратын
тұрақты шама, ал ![]() -жыртқыштың салыстырмалы өлімі. Осы
келтірілген теңдеулерге сәйкес әрбір өзара әсер
етуші популяциялардың санының өсуі басқа
популяциялармен шектеледі, яғни жемтіктің өсу саны
жыртқыштардың санына тәуелді, ал жыртқыштардың
өсу саны жемтік санының жетіспеушілігіне тәуелді.
-жыртқыштың салыстырмалы өлімі. Осы
келтірілген теңдеулерге сәйкес әрбір өзара әсер
етуші популяциялардың санының өсуі басқа
популяциялармен шектеледі, яғни жемтіктің өсу саны
жыртқыштардың санына тәуелді, ал жыртқыштардың
өсу саны жемтік санының жетіспеушілігіне тәуелді.
|
|
2,
б-сурет |
Жоғарыдағы
теңдеулерден құрылған жүйенің шешімі екі
түрлі организмдердің сандарының тұрақты болу
шартын тұжырымдауға мүмкіндік береді. Егер
жыртқыштың тығыздығы ![]() санына тең
болса, онда жыртқыш популяциясының саны тұрақты болады.
Сонымен қатар, жыртқыш популяциясының санын
тұрақты етіп сақтау үшін жемтіктің тығыздығы
санына тең
болса, онда жыртқыш популяциясының саны тұрақты болады.
Сонымен қатар, жыртқыш популяциясының санын
тұрақты етіп сақтау үшін жемтіктің тығыздығы
![]() санына тең болу
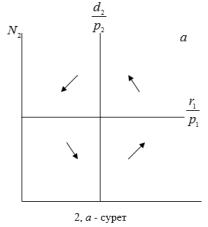
керек. Егер абсцисса өсіне жыртқыштың жиілік саны
санына тең болу
керек. Егер абсцисса өсіне жыртқыштың жиілік саны ![]() -ді, ал ордината өсіне жыртқыштың жиілік
саны
-ді, ал ордината өсіне жыртқыштың жиілік
саны ![]() -ні кескіндесек, онда жемтік пен жыртқыштың
тұрақты болу шарты өзара перпендикуляр болатын екі түзу
арқылы бейнеленеді (2, а-сурет)
-ні кескіндесек, онда жемтік пен жыртқыштың
тұрақты болу шарты өзара перпендикуляр болатын екі түзу
арқылы бейнеленеді (2, а-сурет)
Бұл
жағдайда жемтік пен жыртқыштың ең төменгі
тығыздық деңгейі әрқашан кемиді, ал ең
жоғары деңгейі әрқашан өседі деп
ұйғарылады. Олай болса, егер жыртқыш санының
тығыздығы ![]() -нен кем болса, онда жемтік санының
тығыздығы өседі, ал егер осы саннан үлкен болса, онда
жемтік санының тығыздығы кемиді. Изоклиндердің
қиылысу нүктесі жыртқыштар мен жемтіктердің
сандарының тұрақтылық шартына сәйкес келеді.
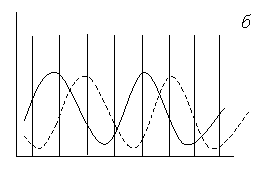
Жазықтықтағы бұл графиктің басқа
нүктелері жыртқыш пен құрбандықтың
регулярлық тербелісін бейнелей отырып, тұйық траекториялы қозғалысты
береді (2, б-сурет).
-нен кем болса, онда жемтік санының
тығыздығы өседі, ал егер осы саннан үлкен болса, онда
жемтік санының тығыздығы кемиді. Изоклиндердің
қиылысу нүктесі жыртқыштар мен жемтіктердің
сандарының тұрақтылық шартына сәйкес келеді.
Жазықтықтағы бұл графиктің басқа
нүктелері жыртқыш пен құрбандықтың
регулярлық тербелісін бейнелей отырып, тұйық траекториялы қозғалысты
береді (2, б-сурет).
Тербеліс
ауытқуының көлемі (құлашы) жыртқыш пен
жемтіктің бастапқыдағы тығыздық санымен
айқындалады. Оның саны изоклиннің қиылысу
нүктесін жақын болған
сайын векторлар арқылы құрылатын шеңберлер
соғұрлым кішірейеді, яғни тербеліс амплитудасы азая береді.
Пайдаланылған әдебиеттер
1. Абатуров Б.Д., Лопатин В.Н. Связь уровня
потребления пищи с размерами тела у растительноядных млекопитающих // Журн.
общ. биологии. 2010.- Т. 48. – № 6. – С. 763-770.
2. Вольтерра В. Математическая
теория борьбы за существование.- М.: Наука, 2014. – 286с.
3. Гиляров А.М. Динамика
численности пресноводных планктонных ракообразных.- М.: Наука. 2012. –
189с.