Пахомов А.А. Валентинов В.А.

Левина Н.В.

Идентификация модели рыночной цены с постоянным коэффициентом эластичности спроса

Identification of a model of market price with a constant coefficient of elasticity of demand

Аннотация.

Приводится доказательство необходимости и достаточности вида функции цены от спроса, имеющей постоянный коэффициент эластичности спроса и рассматривается метод ее идентификации.

Ключевые слова.

Рыночная цена, спрос, эластичность спроса, коэффициент эластичности.

Abstract.

Provides proof of the necessity and sufficiency of the form of the value function of the demand, which has a constant coefficient of elasticity of demand, and it is considered a method of identification.

Keywords.

The market price, demand, elasticity of demand elasticity coefficient.

Коэффициент эластичности спроса определяется по формуле:

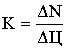(1)

где ΔN – процент изменения объема продаж, ΔЦ – процент изменения цены. При функции спроса с отрицательным коэффициентом эластичности спроса это означает, на сколько процентов увеличится объем продаж, при снижении цены на один процент.

Представим значение коэффициента эластичности спроса в формуле (1) в следующем виде:

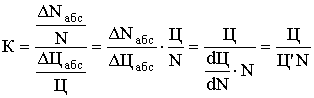(2)

при ΔN_абс → 0, ΔЦ _абс → 0 определяем вид функции Ц=f(N) при условии, что К=const при всех N

Из уравнения (2) имеем:

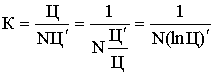(3)

Обозначим Ln Ц = υ, тогда из (3) имеем:

(4)

При условии что К=const, дифференцируя (4) имеем:

(5)

Решим дифференциальное уравнение (5). Обозначим: υ’ = z тогда из (5) получаем:

(6)

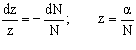где α = const

где β₁ = const

Так как υ = lnЦ получаем ; или положив β₁=lnβ получаем:

(7) То есть функция цены с постоянным коэффициентом эластичности спроса имеет вид, представленный формулой (7). Согласно формуле (2) значение коэффициента эластичности спроса будет в этом случае равно:

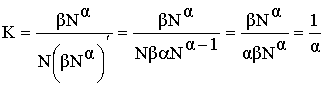, (8)

что является доказательством и достаточности вида функции цены от спроса (7), имеющей постоянный коэффициент эластичности спроса.

Если прологарифмировать обе части выражения (7), то получим:

(9)

lnЦ является линейной функцией от lnN, так как α и lnβ являются константами. Поэтому параметры α и ln β могут быть определены по статистике значений (ln Ц_i; ln N_i) по методу наименьших значений [1. с. 92-96].

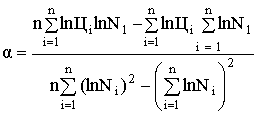(10)

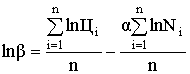(11)

В случае двух значений статистических данных (N₁ Ц₁); (N₂ Ц₂) значения α и β определяются из системы уравнений

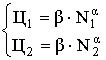(12)

откуда следует, что:

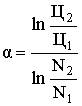(13)

Подставляя полученное по формуле (13) значение α в одно из уравнений системы (12) получим значение β.

Рассмотрим пример по данным, представленным в работе Пастухова Д.В. [2].

Таблица 1 - Данные об объемах продаж и цены для 2-й группы артикулов продукции ЗАО «Московская тонкосуконная фабрика

им. П. Алексеева»

Показатели	Наблюдения
	1	2	3	4
Объем продаж Ni, тыс.п.м.	150	45	44	32
Цена, дол/м Цi	6,52	6,96	7,17	7,62

Результаты расчетов приведены в таблице 2.

Таблица 2 - Расчет коэффициентов α и β в функции цены

№ наблюдения	ln Ni	lnЦi	lnNiּlnЦi	(lnNi)^2
1	5,011	1,875	9,396	25,1101
2	3,807	1,940	7,386	14,4932
3	3,784	1,970	7,454	14,3186
4	3,466	2,031	7,039	12,0131
	Σ=16,068	Σ=7,816	Σ=31,275	Σ=65,9350

Согласно формул (10) и (11) получаем:

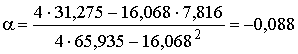
Таким образом, функция цены по данным статистики, представленной в таблице 1 имеет вид: Ц=10,044ּN^-0,088

Коэффициент эластичности спроса согласно формуле (8) равен:

То есть при снижении цены на продукцию на 1% объем продаж возрастает на 11,36%.

График функции Ц=10,044ּN^-0,088 представлен на рис. 1.

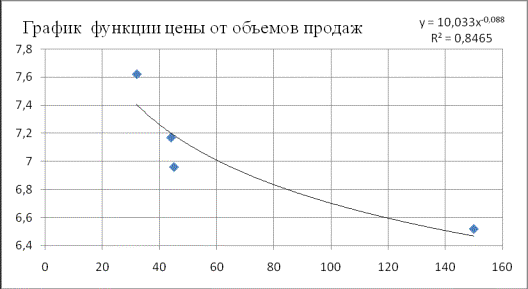
Рис. 1 - График степенной функции цены от объемов продаж вида Ц= α*N^β

На рис. 1 коэффициенты степенной функции находились с помощью графических средств Ехсе1, при этом значение коэффициента β имеет небольшое отличие от «ручных» расчетов, значение коэффициента α совпало с «ручным» расчетом. Коэффициент детерминации равен 0,84, следовательно, 84% исходных данных подчиняется степенной зависимости Ц=10,033ּN^-0,088 [4]

Применение данных видов функций цены от рыночного спроса достаточно полно приведено в работе [3].

Список литературы

1. Кади Дж. Количественные методы в экономике - М.: Прогресс. 1977 с.92-96.

2. Пастухов Д.В., Пахомов А.А. Оптимизация объема производства при маржинальной калькуляции себестоимости продукции с учетом коэффициента эластичности спроса. Сборник научных трудов аспирантов. -.: МГУТУ им. А.Н Косыгина. 2002. – Выпуск 4.

3. Пахомов А.А., Рой Т.Г., Сайдаева А.С. Организационно-экономический механизм формирования системы управления положительной динамикой эффективности работы предприятия. М. : Нестор – История 2014.

4. Валентинов В.А. Эконометрика. Учебное пособие. – М.: Дашков и К, 2010. - 436 с.

5. Вифлеемский А., Левина Н.В. Наукоемкие технологии и система образования. –М. Народное образование, 2004 №9. 6с.