ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ ГИДРОДИНАМИКИ МЕТОДОМ
КОНЕЧНЫХ РАЗНОСТЕЙ
С. Н. Шалтаков, С.
Ш. Кажикенова,
Для компьютерного моделирования течения расплавов
необходимо численное решение уравнений гидродинамики методом конечных
разностей.
Рассмотрим плоское течение. Пусть ![]() область евклидова
пространства
область евклидова
пространства ![]() , причем
, причем ![]() . Разобьем все пространство
. Разобьем все пространство
![]() на элементарные
ячейки, площадь которых:
на элементарные
ячейки, площадь которых: ![]() где
где ![]() шаг.
шаг.
Составим разностные отношения по ![]() :
:
![]()
![]() .
.
Сдвиг по ![]() определим как:
определим как: ![]() .
.
Векторы ![]() представляют собой
единичные векторы по осям
представляют собой
единичные векторы по осям ![]() . Согласно
работе [1] векторы скорости выражаются соотношениями:
. Согласно
работе [1] векторы скорости выражаются соотношениями:
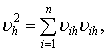
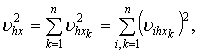
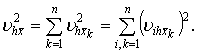
Тогда для произвольных функций ![]() , заданных на сетке,
получим следующие выражения:
, заданных на сетке,
получим следующие выражения:
![]()
![]()
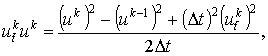
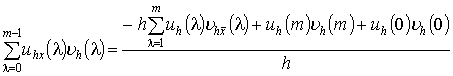 .
.
Здесь принято, что:
![]()
![]()
![]() .
.
Для демонстрации данного метода после соответствующих
преобразований перепишем уравнение гидродинамики в виде:
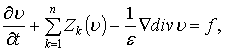 (1)
(1)
где: 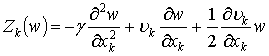 .Для простоты рассмотрим случай, когда
.Для простоты рассмотрим случай, когда ![]() . Для этого разобьем временной интервал
. Для этого разобьем временной интервал ![]() точками:
точками: 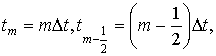
![]() Это позволит
рассмотреть слои
Это позволит
рассмотреть слои ![]() и
и ![]() . Обозначим индексы так, чтобы
. Обозначим индексы так, чтобы ![]() , а также
, а также ![]() указали на номер
слоя, на котором они вычисляются. Существуют различные аппроксимации
разностного оператора
указали на номер
слоя, на котором они вычисляются. Существуют различные аппроксимации
разностного оператора ![]() . Возьмем этот оператор в виде предложенного в работах [2], [3]:
. Возьмем этот оператор в виде предложенного в работах [2], [3]:
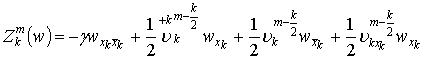 .
.
Тогда уравнение (1) можно представить следующей
разностной схемой:
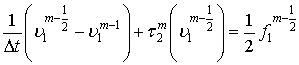 , (2)
, (2)
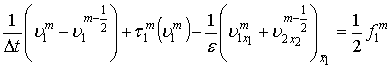 , (3)
, (3)
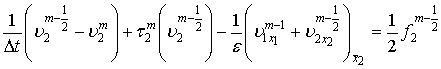 , (4)
, (4)
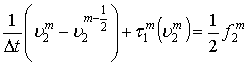 , (5)
, (5)
где ![]() Для полного
завершения построения разностной схемы к этим уравнениям следует добавить
начальные и граничные условия.
Для полного
завершения построения разностной схемы к этим уравнениям следует добавить
начальные и граничные условия.
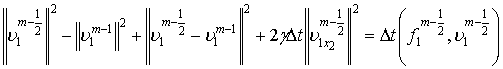 ,
,
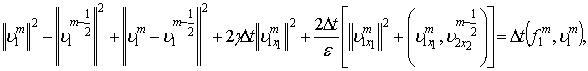
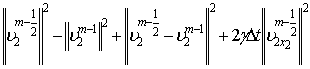
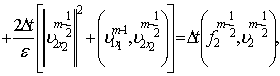
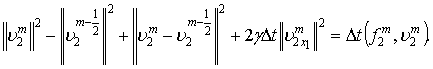 .
.
Таким образом, мы получаем уравнения (2) – (5), которые решаются по отдельности.
Это позволяет написать машинные программы для реализации численных конечно-разностных методов. Для
проверки корректности работы программы решена плоская задача Дирихле для
уравнения Пуассона, приведенного в работе
[4]. Согласно [4],
решение уравнения Пуассона приведено в таблице 1. Для контрольного
примера в таблице 2 приведем решение
задачи Дирихле уже с другими граничными условиями из тех же справочных
источников. Сравнивая решения первой и второй краевых задач Дирихле из
справочных источников, представленными в таблицах 1 и 2, с результатами
программы для решения краевых задач, представленными в таблицах 3 и 4, мы видим
удовлетворительное совпадение решений
при заданной точности ![]() Реализация этой
процедуры занимает 15 минут машинного времени. А при увеличении точности до
Реализация этой
процедуры занимает 15 минут машинного времени. А при увеличении точности до ![]() наши результаты,
представленные в таблице 5, фактически совпадают с результатами стандартных
справочных данных.
наши результаты,
представленные в таблице 5, фактически совпадают с результатами стандартных
справочных данных.
Таблица 1 – Решение первой краевой задачи Дирихле для
уравнения Пуассона из справочных
источников
|
Y |
X |
|||||
|
0.00 |
0.40 |
0.80 |
1.20 |
1.60 |
2.00 |
|
|
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
|
0.20 |
0.08 |
0.32 |
0.51 |
0.72 |
0.99 |
0.84 |
|
0.40 |
0.32 |
0.72 |
1.07 |
1.41 |
1.78 |
1.76 |
|
0.60 |
0.72 |
1.23 |
1.68 |
2.12 |
2.56 |
2.76 |
|
0.80 |
1.28 |
1.82 |
2.65 |
3.22 |
3.82 |
3.84 |
|
1.00 |
2.00 |
2.44 |
2.96 |
3.56 |
4.24 |
5.00 |
Таблица 2 – Решение второй краевой задачи Дирихле для
уравнения Пуассона из справочных источников
|
Y |
X |
|||||
|
0.00 |
0.40 |
0.80 |
1.20 |
1.60 |
2.00 |
|
|
0.00 |
1.00 |
1.40 |
1.80 |
2.20 |
2.60 |
3.00 |
|
0.20 |
2.00 |
1.05 |
0.95 |
1.08 |
1.44 |
2.96 |
|
0.40 |
2.00 |
1.02 |
0.60 |
0.59 |
0.93 |
2.84 |
|
0.60 |
4.00 |
1.36 |
0.78 |
0.63 |
0.93 |
2.64 |
|
0.80 |
5.00 |
2.78 |
2.12 |
1.81 |
1.64 |
2.36 |
|
1.00 |
6.00 |
5.84 |
5.36 |
4.56 |
3.44 |
2.00 |
Таблица 3 –
Решение первой краевой задачи Дирихле для уравнения Пуассона с заданной
точностью ![]()
|
Y |
X |
||||||||||
|
0.000 |
0.200 |
0.400 |
0.600 |
0.800 |
1.000 |
1.200 |
1.400 |
1.600 |
1.800 |
2.000 |
|
|
0.0 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
0.2 |
0.080 |
0.241 |
0.262 |
0.264 |
0.266 |
0.269 |
0.272 |
0.276 |
0.280 |
0.330 |
0.840 |
|
0.4 |
0.320 |
0.303 |
0.301 |
0.303 |
0.305 |
0.308 |
0.311 |
0.315 |
0.320 |
0.447 |
1.760 |
|
0.6 |
0.720 |
0.356 |
0.305 |
0.306 |
0.308 |
0.310 |
0.314 |
0.318 |
0.323 |
0.538 |
2.760 |
|
0.8 |
1.280 |
0.429 |
0.310 |
0.308 |
0.310 |
0.313 |
0.316 |
0.320 |
0.325 |
0.636 |
3.840 |
|
1.0 |
2.000 |
0.523 |
0.315 |
0.311 |
0.313 |
0.315 |
0.319 |
0.323 |
0.329 |
0.741 |
5.000 |
|
1.2 |
2.880 |
0.639 |
0.322 |
0.314 |
0.316 |
0.319 |
0.322 |
0.326 |
0.332 |
0.854 |
6.240 |
|
1.4 |
3.920 |
0.776 |
0.330 |
0.318 |
0.320 |
0.323 |
0.326 |
0.330 |
0.337 |
0.974 |
7.560 |
|
1.6 |
5.120 |
0.935 |
0.341 |
0.323 |
0.326 |
0.329 |
0.332 |
0.336 |
0.343 |
1.105 |
8.960 |
|
1.8 |
6.480 |
1.248 |
0.581 |
0.613 |
0.674 |
0.744 |
0.821 |
0.906 |
1.002 |
1.946 |
10.44 |
|
2.0 |
2.000 |
2.440 |
2.960 |
3.560 |
4.240 |
5.000 |
5.840 |
6.760 |
7.760 |
8.840 |
10.00 |
Таблица 4 – Решение второй краевой задачи Дирихле для
уравнения Пуассона с заданной точностью ![]()
|
Y |
X |
||||||||||
|
0.000 |
0.200 |
0.400 |
0.600 |
0.800 |
1.000 |
1.200 |
1.400 |
1.600 |
1.800 |
2.000 |
|
|
0.0 |
1.000 |
1.200 |
1.400 |
1.600 |
1.800 |
2.000 |
2.200 |
2.400 |
2.600 |
2.800 |
3.000 |
|
0.2 |
2.000 |
1.109 |
1.011 |
1.012 |
1.016 |
1.019 |
1.023 |
1.026 |
1.029 |
1.138 |
2.960 |
|
0.4 |
3.000 |
1.215 |
1.004 |
0.997 |
0.996 |
0.994 |
0.992 |
0.990 |
0.988 |
1.087 |
2.840 |
|
0.6 |
4.000 |
1.325 |
1.007 |
0.997 |
0.995 |
0.993 |
0.991 |
0.988 |
0.985 |
1.074 |
2.640 |
|
0.8 |
5.000 |
1.436 |
1.009 |
0.996 |
0.994 |
0.992 |
0.989 |
0.986 |
0.983 |
1.057 |
2.360 |
|
1.0 |
6.000 |
1.546 |
1.012 |
0.995 |
0.993 |
0.990 |
0.987 |
0.984 |
0.981 |
1.035 |
2.000 |
|
1.2 |
7.000 |
1.656 |
1.015 |
0.994 |
0.992 |
0.989 |
0.986 |
0.983 |
0.979 |
1.008 |
1.560 |
|
1.4 |
8.000 |
1.767 |
1.017 |
0.994 |
0.991 |
0.988 |
0.984 |
0.981 |
0.977 |
0.977 |
1.040 |
|
1.6 |
9.000 |
1.877 |
1.020 |
0.993 |
0.990 |
0.986 |
0.983 |
0.979 |
0.975 |
0.942 |
0.440 |
|
1.8 |
10.00 |
2.018 |
1.059 |
1.027 |
1.022 |
1.016 |
1.009 |
1.000 |
0.992 |
0.917 |
-0.24 |
|
2.0 |
6.000 |
5.960 |
5.840 |
5.640 |
5.360 |
5.000 |
4.560 |
4.040 |
3.440 |
2.760 |
2.000 |
Таблица 5 – Решение первой краевой задачи Дирихле для
уравнения Пуассона с заданной точностью ![]()
|
Y |
X |
|||||
|
0.000 |
0.400 |
0.800 |
1.200 |
1.600 |
2.000 |
|
|
0.00 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
0.20 |
0.080 |
0.301 |
0.508 |
0.750 |
1.001 |
0.800 |
|
0.40 |
0.320 |
0.730 |
1.055 |
1.430 |
1.851 |
1.710 |
|
0.60 |
0.720 |
1.221 |
1.666 |
2.101 |
2.590 |
2.732 |
|
0.80 |
1.280 |
1.790 |
2.599 |
3.202 |
3.798 |
3.884 |
|
1.00 |
2.000 |
2.490 |
2.981 |
3.549 |
4.290 |
5.001 |
Необходимо отметить, что увеличение точности приводит
к возрастанию затрат машинного времени, которое составляет 45 минут. Полученные
результаты показывают корректность составленной программы, а также корректность поставленных краевых задач для
уравнений гидродинамики, рассмотренных нами выше.