Хозіна Д

Силенко В.Є, ст..викладач к.ф.-м.н.

ДонНУЕТ ім. Михайла Туган-Барановського

 

ЗАСТОСУВАННЯ РІВНЯННЯ МОНО ДЛЯ ОПИСУ

ДИНАМІКИ ПОЯВИ ІННОВАЦІЙ

В еволюційній економіці математичні моделі процесів,розглядаються на припущені схожості процесів розвитку біологічних і соціально – економічних систем.

 У роботах [1-3] досліджується  можливість використання S - видних кривих (логістичної, Гомпертца, модифікованої експоненціальної тощо) і рівнянь типу Лоткі - Вольтерра.

Проблема використання логістичних S-видних кривих першого порядку для математичного моделювання полягає в тому, що вони за своїми властивос­тями симетричні відносно точки перегинання.

Логістичні криві добре описують висхідний характер еволюції, але не відбивають ефекту конкуренції на мікро - і мінірівні, а також визначають жорстко детермінований характер розпитку, який немов би не залежить від суб'єктивних чинників, які суперечать реаліям.

Розглянемо математичну модель, яка  описує не­симетричний S-видний характер розвитку соціально-економічних систем,з їхньою постійною питомою швидкістю, модель Мальтуса у поєднанні з рівнянням росту Моно.

 (1)

Де Ks — константа спорідненості субстрата до мікроорганізму, - максимальна швидкість росту біомаси, x- концентрація субстрата.

На рис. 1 показано типову криву, одержану із застосуванням поєднаної моделі Мальтуса-Моно .

 

 

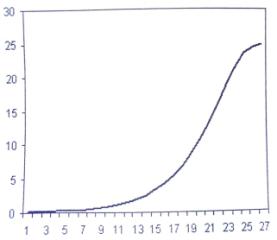
C:\Users\Даша\Desktop\14112010829.jpg

 

Інтерпретація  характеристик цієї  моделі  в соці­ально-економічному аспекті така: концентрація  x — кількість публікацій, присвячена певній проблемі;  S0 - обмежене початкове поле необроблених ідей, яке інтелектуально переробляється в науковий-технічний продукт (публі­кації, патенти) (кантіанська «річ у собі»);  - питома швидкість появи публі­кацій на початку розробки інноваційної проблеми; Ks — концентрація необ­роблених ідей в інформаційному полі, за якої питома швидкість появи публіка­цій змешується вдвічі (ідея починає себе вичерпувати).

Висновки.  S-видні ітераційні моделі Мальтуса-Моно можна застосовувати в тих випадках, коли обмеження на виробництво того чи іншою продукту викликаються обмеженим ресурсом, з якого виробляється продукт.  Наприклад, кількість наукових розробок за обмежених фінансових ресурсів, обсяг інноваційного товару за обмеженої купівельної спроможності населен­ня тощо.

 

 

Література

1.                      Бекбаєва З. Роль и функции средств информационной технологии в активизации самостоятельной учебно-познавательной деятельности учащихся.// Поиск, серия ест. наук. -2001. -№6, - с.113-119.

2.                      Кремер Н.Ш. Теория вероятностей  и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2006.-573 с.

3.                      Городецький В.В., Колісник Р.С.  Про одне узагальнення просторів типу S// Науковий вісник Чернівецького університету: Зб. наук. пр. Вип.134. Ма­тематика. – Чернівці: Рута, 2002. – С. 30-37.