Андрейченко А. Н., Секирин А. И.
Донецкий национальный технический
университет, г. Донецк Украина
Динамический анализ
слабоструктурированных ситуаций на базе триадной модели
Выживаемость
и успешное развитие организационных систем (организаций) в условиях неопределенности
будущего (социальной, экономической, политической, экологической
нестабильности, жесткой конкуренции) зависит от способности менеджмента
предвидеть возможные тенденции изменения ситуации и формировать соответствующие
стратегии развития организации. Ярким примером реализации такой идеологии
является сбалансированная система показателей (ССП), получившая широкую
известность в последнее десятилетие. ССП ориентирована на выявление
стратегических факторов - целей и показателей деятельности, принадлежащих
четырем группам: финансовой, клиентской, внутренних бизнес-процессов, обучения
и развития персонала, а также на установление причинно-следственных связей
между ними.
На
сегодняшний день, известен ряд формальных (математических) моделей и методов
описания и анализа развития слабоструктурированных проблемных ситуаций с учетом
человеческого фактора. В данной работе исследуется возможность применения
таких методов для конкретных задач.
Структура
триадной модели дана на рис. 1, где {![]() }
-множество внешних воздействий на операционный блок; {
}
-множество внешних воздействий на операционный блок; {![]() },
{
},
{![]() }
- множество индикаторов целей и приращений индикаторов целей, соответственно; {
}
- множество индикаторов целей и приращений индикаторов целей, соответственно; {![]() },{
},{![]() }
- множество показателей деятельности и их приращений,
}
- множество показателей деятельности и их приращений,
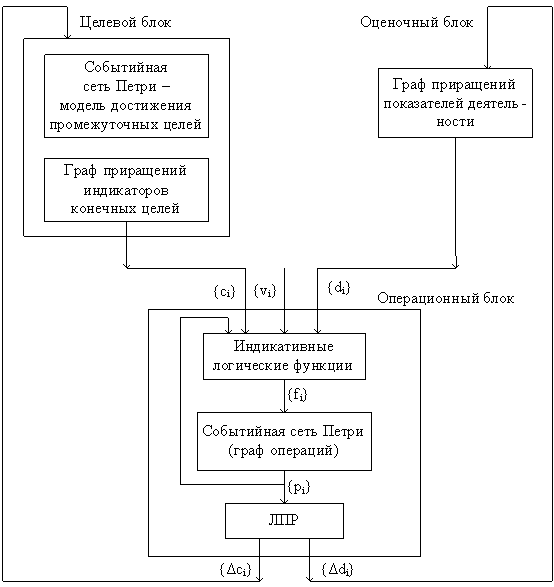
Рисунок 1.
Структура триадной модели
соответственно;
качественные переменные ![]() ,
, ![]() ,
а также их приращения
,
а также их приращения ![]() ,
, ![]() определены на количественной (балльной)
шкале; {
определены на количественной (балльной)
шкале; {![]() }
- множество операций процесса, реализуемого в организационной системе; {
}
- множество операций процесса, реализуемого в организационной системе; {![]() }
- множество событий, инициирующих переходы между операциями, описываются
индикативными логическими функциями; ЛПР - лицо, принимающее решение, которое
для операций процесса задает величину приращений (положительных или отрицательных)
индикаторов целей и показателей деятельности.
}
- множество событий, инициирующих переходы между операциями, описываются
индикативными логическими функциями; ЛПР - лицо, принимающее решение, которое
для операций процесса задает величину приращений (положительных или отрицательных)
индикаторов целей и показателей деятельности.
Событийную
сеть Петри (граф операций) определим как набор S = ![]() ,
где N=
,
где N= ![]() - сеть Петри; Р= {
- сеть Петри; Р= {![]() }
- множество позиций сети, которые в операционном блоке соответствуют операциям
процесса, а в целевом блоке - главной и
}
- множество позиций сети, которые в операционном блоке соответствуют операциям
процесса, а в целевом блоке - главной и
промежуточным целям; T={![]() }
– множество переходов между позициями;
}
– множество переходов между позициями; ![]() - множество дуг;
- множество дуг; ![]() - начальная маркировка сети; Ф={
- начальная маркировка сети; Ф={![]() }
- множество индикативных логических функций
(событий), которые выражаются формулами, составленными из термов вида (
}
- множество индикативных логических функций
(событий), которые выражаются формулами, составленными из термов вида (![]() #
#![]() ),
где х - числовая переменная,
),
где х - числовая переменная, ![]() (рис. 1);
(рис. 1); ![]() - константа; # - знак сравнения, #
- константа; # - знак сравнения, #![]() ,
с помощью логических связок AND(
,
с помощью логических связок AND(![]() ),
OR(v), NEG(
),
OR(v), NEG(![]() );
);
![]() :
T
:
T![]() Ф
Ф![]() -
функция "нагружения" переходов сети Петри функциями
-
функция "нагружения" переходов сети Петри функциями ![]() .
.
Пример событийной сети Петри (заимствован из работы [4] с некоторыми упрощениями) дан на рис. 2. Динамика событийной сети определяется срабатыванием ее переходов.
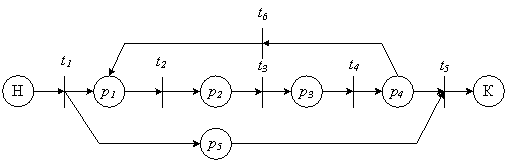
Рисунок 2. Пример событийной сети Петри: н. к - начальная и
конечная позиции; формулы событий (знак ![]() для простоты опущен):
для простоты опущен):
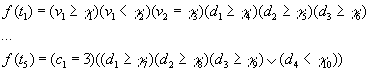
В сети, моделирующей операционный блок, ![]() =
1, если выполняется i-ая операция, и
=
1, если выполняется i-ая операция, и ![]() =
0, если нет. В сети целевого блока маркировка
=
0, если нет. В сети целевого блока маркировка![]() соответствует
уровню достижения цели (например, 1 - низкий, 2 - средний, 3 - высокий уровни).
Переход
соответствует
уровню достижения цели (например, 1 - низкий, 2 - средний, 3 - высокий уровни).
Переход ![]() срабатывает, если все его входные
позиции не пусты и наступает событие
срабатывает, если все его входные
позиции не пусты и наступает событие ![]() =
1. Сеть запускается из заданной начальной маркировки её позиций.
=
1. Сеть запускается из заданной начальной маркировки её позиций.
Граф приращений (ГП)
определим как набор ГП= ![]() ,
где A ={
,
где A ={![]() }
- множество позиций, сопоставленных приращениям факторов (индикаторов конечных
целей и показателей деятельности системы, т. е.
}
- множество позиций, сопоставленных приращениям факторов (индикаторов конечных
целей и показателей деятельности системы, т. е. ![]() {
{![]() });
В ={
});
В ={![]() }
- множество переходов,
}
- множество переходов, ![]() ;
Е
;
Е![]() -
множество дуг, связывающих позиции и переходы,
-
множество дуг, связывающих позиции и переходы, ![]() =
1 (символ позиции со звездочкой слева (справа) обозначает число дуг, исходящих
из позиции (входящих в позицию)); W = {
=
1 (символ позиции со звездочкой слева (справа) обозначает число дуг, исходящих
из позиции (входящих в позицию)); W = {![]() }
- множество весов дуг, ведущих в позиции графа,
}
- множество весов дуг, ведущих в позиции графа, ![]() ]-l,
1[;
]-l,
1[; ![]() :
:
![]() W
- функция "взвешивания" дуг.
W
- функция "взвешивания" дуг.
Рассмотрим правила функционирования графа приращений во времени.
Граф находится в равновесии в момент ![]() , если
, если ![]() =0. Пусть в некоторый момент
=0. Пусть в некоторый момент ![]() >
>![]() вектор
приращений
вектор
приращений ![]() изменится на
изменится на ![]() ,
для которого некоторые компоненты
,
для которого некоторые компоненты ![]() ,
и позиции
,
и позиции ![]() ,
на графе являются непосредственными предшественниками позиций
,
на графе являются непосредственными предшественниками позиций ![]() .
Тогда в момент
.
Тогда в момент ![]() ">
">![]() ' “обнуляем” все ненулевые компоненты (
' “обнуляем” все ненулевые компоненты (![]() ),
а в момент
),
а в момент ![]() '">
'">![]() "
выполняем присваивание
"
выполняем присваивание ![]() ,
т. е. в позиции-последователи вносим маркировки позиций-предшественников в
момент
,
т. е. в позиции-последователи вносим маркировки позиций-предшественников в
момент ![]() ',
умноженные на вес соответствующей дуги. Действия, отнесенные к одному моменту,
выполняются синхронно. Если в позицию-последователь ведет несколько дуг, то
вносимые данные алгебраически суммируются.
',
умноженные на вес соответствующей дуги. Действия, отнесенные к одному моменту,
выполняются синхронно. Если в позицию-последователь ведет несколько дуг, то
вносимые данные алгебраически суммируются.
Выводы.
На
сегодняшний день существует множество литературы посвящено ССП. Вместе с тем,
известен ряд работ, в которых обсуждаются формальные (математические) модели и
методы описания и анализа развития "слабоструктурированных проблемных
ситуаций" с учетом "человеческого фактора" [1...4]. В указанных
работах упор сделан на формальный аппарат нечетких когнитивных карт,
предложенных Коско, хотя эффективно применение и иных математических конструкций.
На основании этого аппарата разработана модель развития сложных организационных
систем в условиях неопределенности и слабой структурированности. Перечисленные
в статье методы целесообразно использовать для анализа слабоструктурированных
проблемных ситуаций в организационных системах.
Литература:
1. Юдицкий С. А.,
Мурадян И. А., Желтова Л. В. Анализ слабоструктурированных проблемных ситуаций
в организационных системах с применением нечетких когнитивных карт// Приборы и
системы. Управление, контроль, диагностика. 2007. № 7.
2. Кульба В.В., Кононов
Д.А., Косяченко С.А., Шубин А.Н. Методы формирования сценариев развития
социально-экономических систем. М.: Синтег, 2004.
3. Kosko В, Fuzzy Cognitive Maps// International Journal of Man-Machine Studies.
1986. № 24.
4. Юдицкий С.А., Желтова
Л.В., Мурадян И.А. Моделирование динамики развития конфигураций
организационных систем на основе сетей Петри и графов приращений // Проблемы
управления. 2007. № 6.