Камнева Д. Н., ст. гр. ЭКИ-07

Науч. руков.: Беличенко А. Ф., к.э.н.,доцент.

Донецкий национальный технический университет, Украина

Оптимизация объёмов производства

В ряде случаев для определения оптимальных размеров промышленных предприятий используют экономико-статистические (регрессионные) модели. Преимущество их состоит в том, что они позволяют оценить возможные варианты объёмов производства предприятий, по которым в настоящее время у экономиста-исследователя отсутствует необходимая информация.

При решении данной задачи наиболее часто используется удельная себестоимость, удельные транспортные расходы и удельные капиталовложения. При этом критерий для нахождения оптимального объёма производства имеет вид:

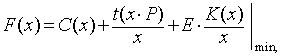(1)

где:

– функция, учитывающая зависимость себестоимости продукции от объёма производства предприятия;

– искомая мощность предприятия;

– плотность сырья в зоне расположения предприятия (количество сырья, приходящееся на квадратный километр площади);

– функция, учитывающая зависимость удельных транспортных расходов от мощности предприятиях и от плотности сырья ;

– нормативный коэффициент эффективности капитальных вложений в отрасли;

– функция, отражающая зависимость удельных капитальных вложений от объёма производствапредприятия.

Сначала определим характер зависимости – себестоимости единицы продукции. При этом эмпирическая линия регрессии весьма близка к гиперболе и описывается уравнением:

(2)

где: и – искомые параметры первого регрессионного уравнения. Для определения этих параметров необходимо с помощью МНК решить следующую систему нормальных уравнений:

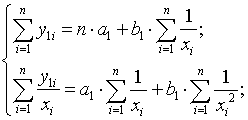(3)

где:

– количество анализируемых предприятий, выпускающих однородную продукцию и входящих в одну отрасль;

– годовой объём производства – го предприятия;

– себестоимость единицы продукции – го предприятия.

Переходим к определению статистической модели для расчёта показателей второго слагаемого критерия оптимальности (1) – удельных транспортных расходов :

(4)

где: и – искомые параметры линейного уравнения. Для определения искомых параметров и необходимо с помощью МНК решить следующую систему нормальных уравнений:

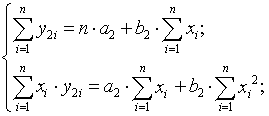(5)

где:

– количество анализируемых предприятий;

– годовой объём производства – го предприятия;

– удельные транспортные расходы – го предприятия.

В заключении определим статистическую модель для третьего слагаемого критерия оптимальности (1) – удельных капиталовложений:

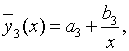(6)

где: и – искомые параметры второго гиперболического уравнения. Эти параметры находятся решением системы нормальных уравнений:

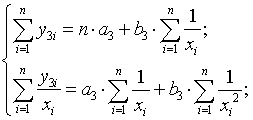(7)

Решим данную задачу для конкретных исходных данных, которые сведены в таблицу 1.

Таблица 1. Исходные данные

, m	, ден.ед.	, ден.ед.	, ден.ед.
11000	248,1	14,7	585,1
35000	160,5	23,8	305,8
55000	139,6	26,3	240,7
75000	122,4	29,7	217,9
135000	118,3	39,8	195,4

С учётом ранее приведённых выражений (1) – (7) и данных табл. 1, произведём расчёт показателя критерия оптимальности (табл. 2).

Таблица 2. Расчётные показатели критерия оптимальности

№ п/п	, m	, ден.ед.	, ден.ед.	, ден.ед.	, ден.ед.
1	11000	250,56	22,34	118,94	391,84
2	35000	153,05	26,90	58,88	238,83
3	55000	136,80	30,70	48,88	216,38
4	75000	129,22	34,5	44,20	207,9
5	100000	124,00	39,25	41,00	204,25
6	110000	122,58	41,15	40,12	203,85
7	120000	121,39	43,05	39,39	203,83
8	135000	119,95	45,90	38,50	204,35
9	150000	118,79	48,75	37,78	205,32
10	200000	116,18	58,25	36,18	210,61

Таким образом, оптимальный объём производства при исходных данных таблицы 1 и заданном критерии оптимальности (1) составляет m (при этом объёме суммарные затраты на производство минимальные и составляют 203.83 ден.ед.). Анализ в табл. 2 произведен при значении коэффициента .

Проведенный анализ позволяет говорить, что оптимизация производства является важнейшей задачей работы предприятия. Однако планированию оптимального объема производства должен предшествовать детальный анализ технико-экономических показателей работы предприятия, который позволит оптимизировать параметры производственного процесса.

Литература:

1. Экономическо-математические методы и модели: Учебн. Пособие /Холод Н.И., Жихар Я.Н. и др.; Под ред. А.В. Кузнецова. – Мн.: БГЭУ, 1999. – 413с.

2. Четыркин Е.М. Статистические методы прогнозирования. Изд. 2-е, перераб. и доп. – М.: Статистика, 1977. – 199с.