Педагогические науки/ 5.Современные методы преподавания

К.ф.-м.н. Толбатов Є.Ю.

Національний авіаційний університет, Україна.

Методика викладання чисельних методів з використанням інформаційного супроводження

Наведено методи рзв’язування нелінійних рівнянь

з однією змінною та систем налінійних рівняньв в

середовищі MathCad та з використанням широко

розповсюджених потужних електронних таблицях

Microsoft Ехсеl для Wiпdows.

Ключові слова. Вбудовані математичні функції, інформаційні технології, матриця Якобі, метод Ньютона, метод перерізуючих, метод дотичних, ітераційний процес, Microsoft Ехсеl для Wiпdows, MathCad.

Постановка проблеми. Обчислювальну техніку останніми роками широко застосовують у всіх сферах діяльності людини. Вона стала каталізатором науково-технічного прогресу. Нагальною є потреба в оволодінні знаннями і навичками використання цієї техніки. Саме тому до програм навчальних закладів введено курс “Основи інформатики та обчислювальної техніки”. Обчислювальні машини можна використовувати ефективно лише за умови глибокого знання чисельних методів математики [1,2]. Чисельні методи покликані озброїти фахівця сучасним інструментарієм розв’язання задач відповідної галузі. Тому викладання чисельних методів повинно здійснюватися з використанням інформаційного супроводження. В дійсний час в Україні відсутні навчальні посібники цього напрямку. В навчальному посібнику по чисельних методах [3] запропоновано методику реалізації деяких методів з використанням мови бейсик. Нажаль, упроваджувати програмування з використанням певної мови не можливо, оскільки в більшості навчальних програм ВНЗ з предмету “Основи інформатики та обчислювальної техніки” не передбачено вивчення мов програмування, але вивчаються електронні таблиці (ЕТ) Microsoft Ехсеl для Wiпdows або пакет програм MathCad. Тому на кафедрі вищої математики НАУ використовують в основному ЕТ Ехсеl [4,5] та MathCad. При реалізації математичної моделі чисельним методом з використанням ЕТ Ехсеl: по-перше, не губиться алгоритм розв’язку задачі; по-друге, студент звільнюється від рутинної роботи розрахунків; по-третє, навчається досконально володіти ЕТ Ехсеl.

Мета дослідження ─ упровадження в учбовий процес інформаційних технологій при розв'язанні задач чисельними методами.

Викладення матеріалу. 1. Розв’язування рівнянь з однією змінною методом Ньютона

Нехай задано рівняння з однією змінною

(1),

де функція визначена і неперервна на деякому відрізку . Необхідно розв’язати це рівняння. Розв’язати рівняння, це означає знайти множину коренів, які належать відрізку . Знайти точні значення коренів можна лише для найпростіших рівнянь. Універсальних методів для знаходження точних значень коренів для алгебраїчних рівнянь степеня та трансцендентних рівнянь не існує. Тому важливого значення набувають наближені методи знаходження коренів рівняння з достатньою точністю. Позначимо через  — точний корінь, а  — його наближення. Корінь наближено обчислено з наперед заданою точністю e, якщо виконується умова .

Знаходження наближених коренів рівняння (1) складається з двох етапів:

1) відокремлення кореня полягає в знаходженні такого відрізка , на якому міститься лише один корінь рівняння;

2) обчислення кореня з наперед заданою точністю.

Для першого етапу не існує досить ефективних методів відокремлення коренів. Для знаходження коренів з наперед заданою точністю застосовують чисельні методи. Корені рівняння можуть бути дійсними і комплексними. Розглянемо наближений метод Ньютона обчислення дійсних коренів рівняння .

Цей метод також називається методом дотичних або методом лінеаризації. Якщо деяке наближення до кореня , а має неперервну похідну, то рівняння (1) можна перетворити наступним чином:

.

Замінюючи на значення похідної від функції у точці , а х на отримаємо наступну ітераційну формулу Ньютона:

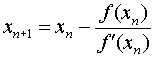(2)

Геометрично цей процес означає заміну на кожній ітерації графіка дотичною до нього (рис. 1). Тобто наближення дістали як абсцису точки перетину осі і дотичної до графіка функції в точці . Відповідно наближення дістали як абсцису точки перетину осі і дотичної до графіка функції в точці .

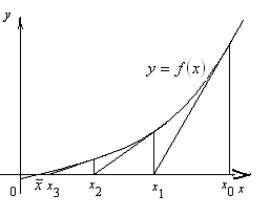
Рис. 1. Геометрична інтерпретація методу Ньютона

Сформулюємо умови збіжності ітерації. Якщо нульове приближення вибране досить близько до кореня, ньютонівські ітерації збігаються. Швидкість збігання велика для простого кореня і відповідає швидкості геометричної прогресії для ратного кореня. При довільному нульовому наближенні ітерації збігаються, якщо скрізь виконується нерівність ,

в протилежному випадку збіжність буде не при будь-якому нульовому наближенні, а тільки в деякому околі кореня.

Збіжність поблизу будь-якого кореня монотонна, але на віддалі від кореня можлива немонотонність ітерації. Відмітимо ще достатню умову збіжності ітерації. Нехай справа від кореня на відрізку . Якщо вибрано також справа від кореня на цьому відрізку, то ітерації (2) збігаються, до того ж монотонно. Те ж саме буде, якщо зліва від кореня на відрізку і на цьому ж відрізку вибране нульове наближення. Таким чином, ітерації збігаються до кореня з того боку, з якого .

Для знаходження коренів довільної диференційованої функції частіше за все використовують метод Ньютона, особливо якщо відомі різні початкові приближення для коренів.

Приклад. Розв’яжемо нелінійне рівняння, використовуючи метод Ньютона

.

Використаємо формулу: .

Для цього знайдемо похідну функції по змінній x:

,

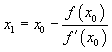та складемо таблицю в ЕТ Excel (табл. 1). За початкове значення візьмемо 1: . Це значення вводимо в комірку А4. Значення функції знаходимо в комірці В4 за формулою: =А4^4+4*A4^3- A4^2-16*A4-12. Відповідно, значення знаходимо в комірці С4 за формулою: =4*A4^3+12*A4^2-2*A4-16. Знаючи значення , , , знаходимо в комірці А5 x1 за формулою (=A4-B4/C4). Ознаку закінчення ітераційного процесу вводимо в комірку D5 за формулою .

Введені формули копіюємо доти, доки не отримаємо значення <0,00001. Після чого отримаємо результат — перший корінь рівняння. Виключаємо його із початкового рівняння за схемою Горнера. Схема Горнера полягає у виключені кореня із многочлена.

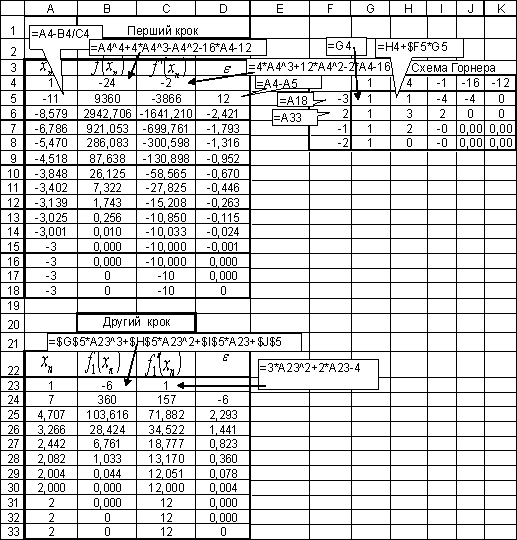
Таблиця 1

Розв’язання рівняння з однією змінною за методом Ньютона

Нехай рівняння має вигляд:

і має корінь . Тоді цей многочлен ділиться націло на вираз . Це ділення зручно виконувати в ЕТ Excel за схемою Горнера. Після ділення на , порядок многочленна зменшиться на одиницю і коефіцієнти многочленна

визначаються за формулами: .

Значення коефіцієнтів вихідного многочленна розташовані у діапазоні комірок G4:K4 (табл.1). У комірку H5 вводимо формулу =H4+$F5*G5 для розрахунку і копіюємо введену формулу в решту комірок цього рядка. В діапазоні комірок G4:J4 дістанемо коефіцієнти наступного рівняння , яке не містить кореня і містить решту коренів вихідного рівняння. Один із коренів цього рівняння знаходимо аналогічно попередньому в діапазоні комірок А22:D33 (). За схемою Горнера в діапазоні комірок G6:I6 знаходимо коефіцієнти квадратного рівняння . Наведене рівняння має чотири дійсних кореня (–3, –2, –1, 2).

2. Розв’язування рівнянь з однією змінною методом перерізуючи

Метод перерізуючи полягає в заміні похідної в ітераційній формулі Ньютона кінечними різницями (відношення приросту функції до приросту аргументу):

.

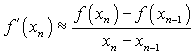Після заміни похідної функції кінечними різницями дістанемо рекурентну формулу:

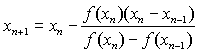.                    (3)

Для початку процесу необхідно задати та .

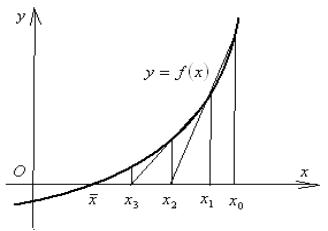
Рис. 2. Геометрична інтерпретація метода перерізуючих

Такі процеси, де для визначення наступного наближення необхідно знати два попередніх, називають двокроковими. Геометрично наближення дістали як абсцису точки перетину осі і січної, що проходить через точки і графіка функції (рис. 2). Відповідно наближення дістали як абсцису точки перетину осі і січної, що проходить через точки і графіка функції .

Збіжність ітерацій може бути немонотонною не тільки далеко від кореня, але й поблизу нього. Швидкість збігання також змінюється. Метод перерізуючих збігається повільніше, але в методі Ньютона на кожній ітерації необхідно обчислювати і функцію і її похідну, а в методі перерізуючих тільки функцію. Тому при однаковому об’ємі обчислень в методі перерізуючих можна зробити вдвічі більше ітерацій і отримати більш високу точність. В знаменнику формули (3) стоїть різниця значень функції. На віддалі від кореня це не суттєво, але поблизу кореня, особливо кореня високої кратності, значення функцій малі і дуже близькі. Виникає втрата значущих цифр, що призводить до «розхитування» розрахунку. Це обмежує точність, з якою можна знайти корінь. Для простих коренів це обмеження не велике, а для кратних коренів може бути суттєвим.

3. Розв’язування рівнянь з однією змінною в середовищі MathCad

Нелінійне рівняння у вигляді многочлена можна розв’язувати в MathCad з використанням вбудованої функції polyroots. Якщо рівняння у вигляді многочленна має вигляд , то вихідні дані задаються у вигляді вектора-стовпчика, в якому першим знизу є значення , а останнім — . Командою fx /polyroots знаходимо корені рівняння у вигляді вектора-стовпчика.

Ця програма дозволяє знаходити не лише дійсні, але й комплексні корені многочленна.

Приклад. Розв’яжемо рівняння , використовуючи в MathCad вбудовану функцію polyroots(v), де V — вектор-стовпчик створений з коефіцієнтів многочлена записаних в зворотному порядку.

, .

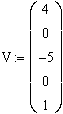Корені наведеного рівняння відповідно мають значення: –2, –1, 1, 2.

Порядок використання функції polyroos:

1. Спочатку записуємо рівняння у вигляді многочлена.

2. Привласнюємо змінній V вектор-стовпчик, в якому знаходяться коефіцієнти при х, тобто: , причому останнім елементом вектор-стовпчик має бути значення .

3. Відкриваємо fx/Решение/polyroots. Ця функція повертає вектор-стовпчик, який містить всі корні рівняння, коефіцієнти якого знаходяться в векторі V.

4. Розв’язання системи нелінійних рівнянь за методом Ньютона

Розглянемо систему нелінійних рівнянь:

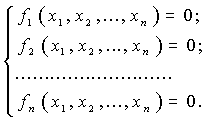
або , .

Знайдемо розв’язок системи нелінійних рівнянь за методом Ньютона.

За початкове наближення приймемо деякі значення:

, або .

Якщо через позначимо неув’язку коренів, тобто різницю між точними значеннями коренів рівняння і початковим наближенням, то розв’язок системи нелінійних рівнянь можна записати у вигляді:

, або .

Записаний розв’язок має задовольняти кожне нелінійне рівняння системи.

Наприклад, перше рівняння набуде вигляду:

Розкладемо ліву частину цього рівняння в ряд Тейлора в точці початкового наближення за степенями неув’язок:

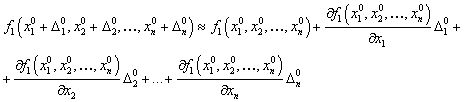
Оскільки неув’язки вибрані таким чином, що функція в точці дорівнює нулю, то із попереднього виразу дістанемо рівняння:

Аналогічним чином дістанемо решту лінійних рівнянь відносно неув’язок . Таким чином дістанемо систему лінійних рівнянь відносно неув’язок:

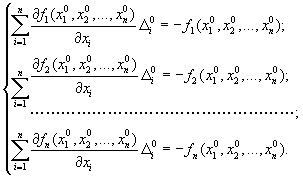
Матрицею цієї системи лінійних рівнянь є матриця Якобі в точці Якщо через позначити точку початкових наближень , через

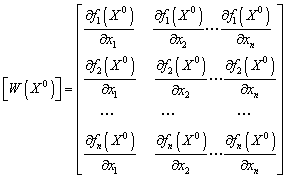
матрицю системи і через вектор неув’язок, то система лінійних рівнянь запишеться в наступній матричній формі: ,

де — вектор функцій в точці .

Якщо визначник матриці відмінний від нуля, то вектор неув’язок можна знайти за формулою:

(4)

Наближений розв’язок системи нелінійних рівнянь набуде значень

.

Вибравши за початковий розв’язок , знайдемо аналогічним чином , і відповідно .

Таким чином, для знаходження наближеного розв’язку системи нелінійних рівнянь маємо рекурентну формулу:

. (5)

Отриманий алгоритм зручно реалізувати в ЕТ Excel, використовуючи вбудовані математичні функції МОБР і МУМНОЖ. Для цього необхідно задати вектор початкових наближень і ввести його координати у визначений діапазон комірок. Знайти значення елементів матриці Якобі і вектор функцій .

На основі введених даних, за формулою (1), знайти вектор неув’язок:

, а потім перший наближений розв’язок . Використовуючи можливість копіювати рекурентні формули з відносними адресами, отриману частину розрахунків копіюємо доти, доки не дістанемо задану точність , де e — задана точність розрахунків коренів системи нелінійних рівнянь.

Приклад. Розв’яжемо систему нелінійних рівнянь за методом Ньютона:

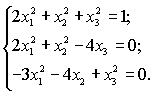
Знаходимо Якобіан. Оскільки , то частинні похідні першого порядку будуть мати вигляд:

Аналогічним чином знаходимо решту частинних похідних.

Якобіан буде мати наступний вигляд:

.

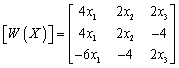Нехай початкові значення знаходяться в діапазоні комірок B2:D2 (табл. 2). Значення Якобіана введемо в діапазон комірок B4:D6. Наприклад, частинна похідна знаходиться в комірці B4 за формулою =2*В2, оскільки початкове значення знаходиться в комірці B2. Аналогічним чином вводимо решту елементів якобіана.

Таблиця 2

Розв’язання системи нелінійних рівнянь за методом Ньютона

Значення функцій знаходимо в діапазоні комірок G4:G6 за відповідними формулами, наприклад, в комірку G4 вводимо формулу:
=-(2*B2^2+C2^2+D2^2-1). Значення визначника матриці системи лінійних рівнянь знаходимо в комірці F6, використовуючи вбудовану математичну функцію МОПРЕД. Неув’язки знаходимо в діапазоні комірок В8:В10, ввівши складену формулу =МУМНОЖ(МОБР(B4:D6);G4:G6). Для зручності запису , записуємо вектор відхилень у вигляді рядка. Для цього використовуємо вбудовану функцію ТРАНСП(B8:B10).

Для знаходження першого наближення в комірку В14 вводимо формулу =В2+Е9 і копіюємо її по рядку в необхідну кількість комірок.

Задаємо точність ε = 0,001 в комірці D11. Для перевірки визначення розв’язку із заданою точністю в комірку F11 вводимо формулу
=ЕСЛИ(МАКС(ABS(E9:G9))<=$D$11; «закінчити цикл !»; «продовжити цикл !»).

Якщо маємо запис «продовжити цикл», то копіюємо діапазон комірок А4:G14 і поставивши курсор на комірку А15, виконуємо команду «Вставить».

Описану процедуру копіювання продовжуємо доти, доки не дістанемо розв’язок із заданою точністю, тобто не дістанемо команду «Закінчити цикл!» (продовження 1 табл. 2).

Продовження 1 таблиці 2

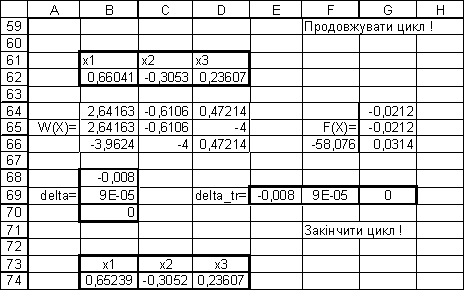
У діапазоні комірок В74:D74 знаходиться один із наближених розв’язків системи нелінійних рівнянь: , , . Задаючи початкові значення для змінних з протилежними знаками (–1, –1, –1), знайдемо інші розв’язки системи нелінійних рівнянь: , , .

Знайдемо розв’язки цієї задачі з використанням програми Поиск решения. Задамо початкові значення для змінних в діапазоні комірок B2:D2 відповідно (1, 1, 1). Відповідні рівняння в діапазоні комірок В4:В6. В діалоговому вікні Поиск решения в текстовому полі цільової функції відмічаємо одну із комірок, в яких задані функції, наприклад В4. В текстовому полі обмеження записуємо умову рівності правої та лівої частин рівнянь, тобто В4:В6 = 0. У діапазоні комірок В2:D2 дістанемо розв’язок системи нелінійних рівнянь, що відповідають даним початковим умовам. Для отримання іншого розв’язку системи нелінійних рівнянь, що відповідають іншим початковим умовам, копіюємо задані умови системи нелінійних рівнянь (діапазон комірок А1:Е6) і вставляємо в діапазон комірок А8:Е13. Задамо початкові умови з протилежними знаками і знайдемо розв’язок, використовуючи програму Поиск решения.

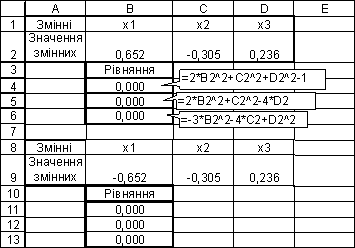
Таблиця 3

Розв’язок системи нелінійних рівнянь з використанням програми

«Поиск решения»

Література:

1. Н.Н.Калиткин. Численные методы. Главная редакция физико-математической литературы издательства “Наука”, М., 1978.

2. Б.П.Демидович, И.А.Марон, Э.З.Шувалова. Численные методы анализа. Главная редакция физико-математической литературы издательства “Наука”, М., 1967.

3. М.Я.Лященко, М.С.Головань. Чисельні методи: Підручник. – К.: Либідь, 1996. – 288 с.

4. Ю.А.Толбатов, Є.Ю.Толбатов. Математичне програмування: Підручник для студентів екон. спеціальн. вищ. навч. зал. – Тернопіль: Підручники і посібники, 2008. – 432 с.

5. Ю.А.Толбатов, Є.Ю.Толбатов. Елементи лінійної алгебри та аналітичної геометрії: навчальний посібник. – К: Четверта хвиля, 2002. – 192 с.