Технические науки

6. Электротехника и радиоэлектроника

Горская И.Ю., Иванько Д.С.

Таврический национальный университет им. В.И.Вернадского, Украина

Методика расчета поля магнитной линзы

В последнее время интерес и актуальность вопросов, связанных с технологией создания и оптимизацией устройств на постоянных магнитах, значительно возросли вследствие появления на рынке высокоэнергетичных и недорогих магнитотвердых материалов на основе Nd-Fe-B. Показатели таких магнитов лишь незначительно уступают показателям электромагнитов, применяемых в электрических машинах с магнитоэлектрическими индукторами.

Настоящая работа посвящена расчёту поля в рабочей области магнитной линзы, выполненной из закритического материала. Такие магниты имеют высокую коэрцитивную силу по индукции и по намагниченности, петля гистерезиса для них имеет почти прямоугольную форму. Они обладают высокой устойчивостью к размагничивающим полям, поэтому можно считать, что при их работе распределение вектора намагниченности не изменяется.

Рассмотрим магнит в виде тора прямоугольного сечения, вектор намагниченности которого параллелен оси. Для расчета будем использовать зарядовую модель, в соответствии с которой поле определяется по формуле:

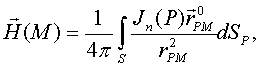
где S – поверхность магнита; – нормальная компонента вектора намагниченности на поверхности магнита S; P – точка на поверхности магнита; M – произвольная точка пространства; - расстояние между точками P и M; .

В рамках зарядовой модели магнитная линза эквивалентна двум параллельным шайбам, равномерно заряженным с поверхностной плотность зарядов где - проекция вектора намагниченности на внешнюю нормаль. В свою очередь, каждую из шайб можно представить как совокупность элементарных колец. Поэтому возникает вспомогательная задача расчета поля равномерно заряженного кольца. Выражения для компонент поля кольца в точке с координатами (r,z) имеют следующий вид:

где - линейная плотность заряда; R – радиус кольца; K(k) и E(k) – эллиптические интегралы первого и второго рода соответственно; k – модуль эллиптического интеграла: . Просуммировав вклады элементарных колец, получим поле двух шайб, т.е. поле тороидального магнита.

Указанная методика расчета поля была реализована для постоянного магнита со следующими параметрами:

· внутренний радиус 50 мм;

· внешний радиус 70 мм;

· толщина магнита 20 мм;

· остаточная индукция магнитотвердого материала 1,05 Тл;

· радиус рабочей области 49 мм;

· длина рабочей области 40 мм.

На рисунках 1 и 2 приведены графики функций и . Из данных графиков видно, что компонента , по сравнению с компонентой , существенно меньше. На рисунке 3 приведен график функций . Данный график указывает на то, что поле принимает максимальное значение в центральной части рабочей области.

Рис 1. График функции

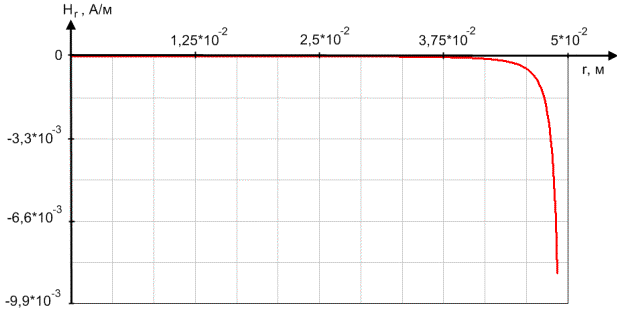
Рис 2. График функции

Рис 3. График функции

Рассмотренный постоянный магнит в дальнейшем будет использован как деталь при сборке осесимметричной магнитной системы. И, следовательно, умея рассчитывать поле одного элемента, на основании принципа суперпозиции, можно будет рассчитать поле всей конструкции.

Литература:

1. Смайт В. Электростатика и электродинамика – М. Издательство иностр. лит., 1954. 604 с.

2. Тозони О.В. Маеройз И.Д. Расчет трёхмерных электромагнитных полей. – Киев: Техника, 1974. – 352 с.

3. Постоянные магниты: Справочник \ Под ред. Пятина Ю.М. – М.: Энергия, 1980. - 488с.

4. Справочник по специальным функциям \ Под ред. Абрамовица М. и Стиган И., ‑ М.: Наука, 1979.

5. Двайт Г.Б. Таблицы интегралов и другие математические формулы. – М. Наука, 1966. – 288 с.