Мельник В.Н., Карачун В.В.

Национальный технический университет Украины «КПИ»

слоистая преграда в акустическом поле. одномерная задача

Слоистые среды — частный случай неоднородных сред, свойства которых существенно изменяются вдоль одной координаты — перпендикулярно плоскостям слоев. Структура многослойных конструкций определяется количеством, размерами и физико-механическими свойствами слоев, а также общей толщиной, которая либо фиксирована, либо устанавливается с помощью методов оптимизации по выбранному критерию качества.

Задачи оптимального проектирования конструкций из конечного набора материалов обладают особенностями, не позволяющими эффективно использовать для их решения, например, методы математического программирования и некоторые другие. Если анализировать плоские панели с числом слоев не более , которые можно составить из т материалов, то количество вариантов будет равно . Вместе с тем, с помощью ПЭВМ, за ограниченное время можно рассмотреть множество вариантов оптимального сочетания слоев и решить задачу в общем виде. Сузим задачу исследований и выберем самый простой из всех возможных вариантов, а именно, плоскую трехслойную конструкцию.

Рассмотрим прохождение звука через бесконечную по протяженности пластину, что дает возможность для определенных условий решать плоскую задачу и использовать одномерные уравнения при построении математической модели трехслойной конструкции с жестким заполнителем.

Механическая модель прохождения звуковой волны через трехслойную преграду представлена на рис. 1.

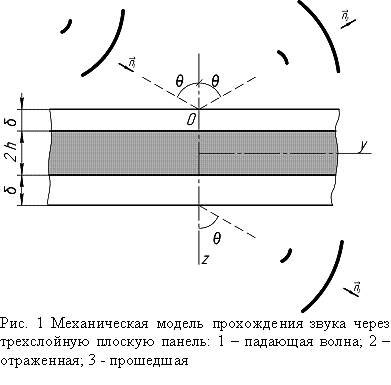
Пусть звуковое давление в падающей, отраженной и прошедшей волнах изменяется по законам:

Тогда, пренебрегая нелинейными членами, одномерную математическую модель антисимметричных и симметричных колебаний можно записать в виде :

(1)

(2)

где , соответственно антисимметричная и симметричная составляющие прогиба трехслойной пластины; , − прогибы срединных плоскостей верхней и нижней пластины; − угол поворота плоских сечений заполнителя; − тангенциальные составляющие перемещений срединной плоскости заполнителя; штрихами и точками обозначены соответственно производные по координате и по времени;

и — модули упругости, коэффициент Пуассона и плотность материала соответственно несущих слоев и заполнителя; — модуль сдвига заполнителя; .

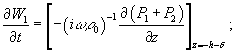
С учетом равенства колебательных скоростей обеих пластин нормальным составляющим колебательных скоростей воздуха, граничные условия можно записать в виде:

где — плотность воздуха.

Учитывая, например, только потери энергии в заполнителе и пренебрегая затуханием в пластинах, можно записать закон изгибных колебаний нижней пластины, как представляющей больший практический интерес, в виде:

(3)

где

В силу того, что граница раздела двух сред с разными физико-механическими свойствами служит генератором отраженных и прошедших волн, можно с помощью слоистых (а в общем случае неоднородных) конструкций существенно влиять на волновую картину процесса, изменяя параметры слоев. При этом определяющими могут оказаться свойства дисперсии, диссипации и многолучевой интерференции составных элементов.

Задача оптимального проектирования слоистых систем, таким образом, будет сводиться к обеспечению наилучших значений этих параметров.

Помимо прочего, становится возможным решение задач получения неотражающих переходных слоев между средами, а также оптимизации геометрических и массовых характеристик конструкции в целом и др.