Касенов А.Ж.

Павлодарский Государственный университет им. С. Торайгырова, г. Павлодар

Республика Казахстан

Математическое описание процесса обработки отверстий развёрткой-протяжкой

Развёртка-протяжка в отличие от протяжек с винтовым зубом имеет конусную режущую часть. Угол конуса зависит от величины снимаемого припуска.

При обработке отверстий развёрткой-протяжкой каждый её зуб от начала до конца постоянно участвует в работе, что обеспечивает стабильность силы резания. Также заготовке или развёртке-протяжке в зависимости от способа обработки имеется вращательное движение с моментом М_кр, возникает «скользящее» резание. Величина силы резания Р является постоянной: .

Дифференциальное уравнение обработки отверстий развёрткой-протяжкой принимает вид уравнения (1), общее решение которого относительно скорости резания решается аналогично

(1)

График переходного процесса, длительность которого составляет (рисунок 1)

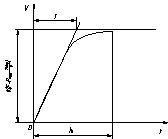
Рисунок 1 – График переходного процесса.

В случае, если материал детали анизотропен (имеются включения повышенной или пониженной твёрдости), то сила протягивания будет меняться.

Пусть сила протягивания , где – постоянная составляющая силы протягивания; – переменная составляющая силы протягивания.

Для возможности математического описания процесса полагаем изменения Р_Δ по закону косинуса, то есть в момент контакта процессе работы меняется от 0 до Р.

Тогда процесс обработки будет описываться следующим дифференциальным уравнением

, (2)

где с – коэффициент упругости материала;

w – частота внутренних колебаний.

Механическая система такого процесса представлена на рисунке 2.

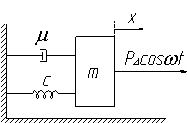
Рисунок 2 – Механическая модель системы.

Её структурная схема через передаточную функцию

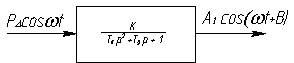
Рисунок 3 – Усиление амплитуды .

В передаточной функции постоянная времени, способствующая колебанию системы , – постоянная времени, стремящаяся часть колебания на выходе и В – сдвиг фазы.

Если – это звено будет апериодическим второго порядка и передаточная функция будет иметь вид:

, (3)

где и .

Амплитудно-фазовая характеристика (при )

(4)

Откуда модуль, которого даёт усиление амплитуды

(5)

Фазовая частотная характеристика

(6)

Если , то звено будет колебательным

(7)

При этом

(8)

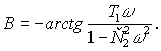(9)

Амплитудно-частотная, фазо-частотная и амплитудно-фазочастотная частотная характеристики представлены на рисунках 4 – 6.

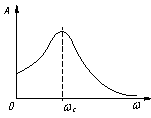
Рисунок 4 – Амплитудно-частотная характеристика системы.

Из рисунка 4 следует, что необходимо вести обработку в зарезонансном режиме при .

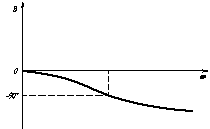
Рисунок 5 – Фазо-частотная характеристика системы.

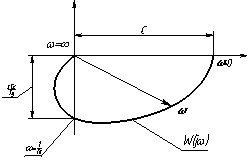
Рисунок 6 – Амплитудно-фазочастотная характеристика системы.

Таким образом, получены следующие выводы

1 Переходной процесс обработка отверстия протяжкой с винтовыми зубьями, показывающий изменение скорости резания (1), происходит по экспоненте график на рисунке 1, длительность которого влияет на точность обработки, можно снизить, уменьшая массу движущихся частей m.

2 Процесс обработки отверстия развёрткой-протяжкой описывается дифференциальным уравнением (2), решение которого при , позволяет построить амплитудно-частотную характеристику (3) и при – амплитудно-частотную характеристику (7) рисунок 4, из которой видно, что амплитуда колебания инструмента растёт с увеличением частоты колебания w достигая максимума при w=w_с, а затем её значение уменьшается. Поэтому рекомендуется осуществлять обработку отверстия за резонансной зоне, w>>w_c.

3 Разработанная конструкция развёртки-протяжки для обработки цилиндрических отверстий обеспечивает повышение качества поверхности отверстия и улучшение условий резания, т.е. работа резания распределена на большей длине режущих кромок за счёт конусности режущей части. При этом уменьшается толщина среза, удельная деформация и температура.