Технические науки. Автоматизированные

системы управления на производстве

Тимонин Д.В.

Самарский Государственный Университет Путей Сообщения

Алгоритм параметрической идентификации в условиях минимальной априорной информации об особо аддитивных помехах наблюдений

Рассмотрим стационарную нелинейную динамическую систему, которая описывается следующим разностным уравнением:

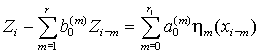, (1)

где выходная переменная наблюдается с аддитивными помехами в виде:

Требуется по наблюдаемым конечным выборочным реализациям последовательностей и при известных порядках и (1) определить оценки истинных значений параметров.

В [1] показано, что для получения состоятельных оценок параметров (1) применим следующий критерий:

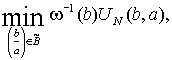(2)

где - компакт, ,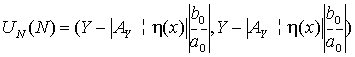

- скалярное произведение, ,

, , ,

,,

, ,

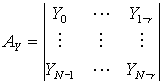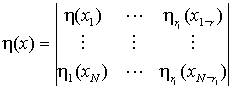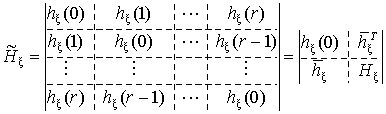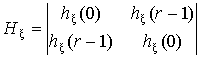Для получения численного метода вычисления оценок параметров из критерия (2) рассмотрим функцию:

,

,

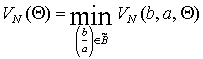тогда

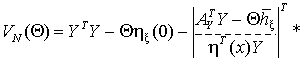
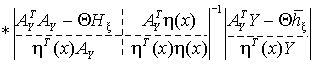(3)

Заметим, что на интервале непрерывна, где наименьший корень уравнения:

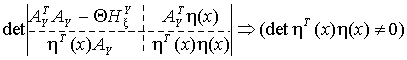
Далее

,

где

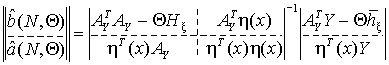(4)

И что, на

Следовательно, корень существует, находится на интервале и является наименьшим, среди всех корней уравнения .

Уравнение (3) можно записать в виде:

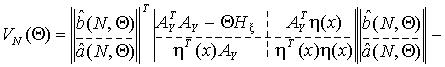
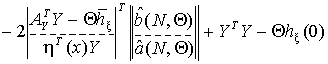
Рассмотрим особенности численных методов определения оценок параметров:

Лемма 1. Для функции справедливы следующие утверждения:

1. Все корни уравнения (если они существуют) неотрицательны

2. Уравнение на полусегменте имеет не более одного корня, если , где - наименьшее обобщенное собственное число матрицы (4)

(5)

3. Непрерывность матрицы и существование корня на интервале является необходимым и достаточным условием существования единственного решения (2), при этом:

,

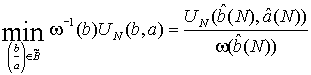где 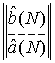определяется уравнением (4)

Эта лемма практически доказана, если учесть условие утверждения 1 [1].

Утверждение 1.

Пусть последовательность определяется следующим алгоритмом:

Шаг 0. .

Шаг 1. , определяется из (5).

Шаг 2. Вычислить и из системы уравнений:

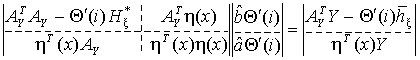(6)

Шаг 3. Вычислить

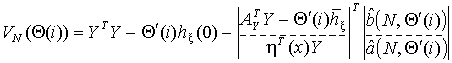
Шаг 4. Проверить условие .

Тогда, если уравнение имеет корень , то последовательность конечна и , в противном случае она бесконечна.

Доказательство утверждения 1 немедленно следует из леммы 1.

Этот алгоритм позволяет определить начальное приближение , необходимое для дальнейшего применения метода Ньютона или определить, что корень не существует.

Утверждение 2.

Пусть существует , тогда

, , ,

где , и определяются совместно следующим алгоритмом.

Шаг 1. Вычислить и из системы уравнений (6).

Шаг 2. Вычислить

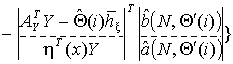
Шаг 3. Переход к шагу 1.

Вычисления заканчиваются, если выполняется условие:

,

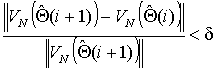где - априорно заданная точность нахождения оценки.

Это утверждение непосредственно следует из метода Ньютона:

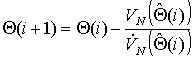
Обоснованность использования метода Ньютона вытекает из того, что функция непрерывна на интервале и, и на интервале .

На основе вышеописанного алгоритма создано программное обеспечение, позволяющее получать оценки матриц параметров с наперед заданной точностью.

Литература:

1. Кацюба О.А., Тимонин Д.В. “Математические методы в технике и технологиях ММТТ-21” – Численный метод идентификации параметров нелинейных динамических систем при наличии помех наблюдений // Сборник трудов «Математические методы в технике и технологиях - ММТТ-21». – Саратов: Изд-во Сарат. гос., 2008. – Т. 2.