Математика / 4. Прикладная математика

К.ф.-м.н. Быкова И.Ю.

Восточно-Казахстанский государственный технический университет, Зыряновский центр, Республика Казахстан

АППРОКСИМАЦИОННАЯ СХЕМА ДЛЯ МОДЕЛИ MSP-M, ТЕОРЕМЫ О СХОДИМОСТИ

Рассмотрим одноэтапную задачу стохастического программирования с совместными вероятностными ограничениями

(STO 1)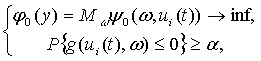

где -скалярная функция; – -мерная вектор-функция; ;

– множество реализаций случайной величины , -вероятностное пространство с заданной мерой .

Предположим для начала, что , и выпукла. Зафиксируем , построим последовательности и , где -функция, обратная функции распределения случайной величины

Рассмотрим семейство задач

SIP(n)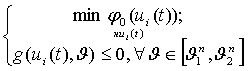

Пусть – решение задачи SIP(n).

Обозначим через оптимум задачи SIP(n). Определим также . Пусть – решение STO 1. Тогда при выпуклой функции множество -замкнутый интервал вида .

Сформулируем условия при которых может являться оценкой оптимума задачи STO 1.

Пусть

А) строго выпуклы по всем своим переменным;

Б) для и существуют и непрерывны первые производные;

В) существует

Г) существует

Д) для случайной величины существует дифференцируемая функция распределения F(u_i(t));

Е) существует

Ж) существует решение задачи STO 1 , причем

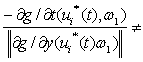
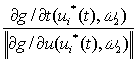
тогда,

В случае векторной случайной величины в предположении независимости составляющих .

Пусть

А) строго выпуклы по всем своим переменным;

Б) для и существуют и непрерывны первые производные;

В) существует

Г) существует

Д) для случайной величины существует дифференцируемая функция распределения , такая, что

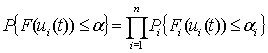
Е) существует

Ж) существует решение задачи STO 1, причем

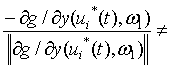
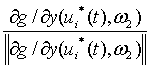
тогда, .

Построим теперь семейство аппроксимационных задач для задачи -го этапа модели MSP-M.

Предположим, что . Обозначим через вектор-функцию распределения случайной величины , причем предположим составляющие независимыми, т.е.

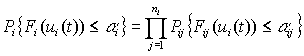(26)

Обозначим через функцию, обратную -й составляющей функции распределения случайной величины .

Для фиксированной рассмотрим последовательности

И для _.

Рассмотрим семейство задач для фиксированного .

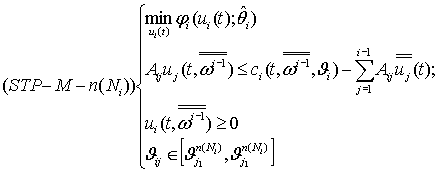
Решение задачи (SIP-M-n(Ni)) будем обозначать через (SIP-M-n(Ni)), оптимальное значение функционала на этом решении обозначим через .

Определим

Пусть

1. Функция строго выпукла по , функция строго выпукла по

2. Существует и равномерно по непрерывны первые производные функций и

3. Существует такая, что для любых

4. Существует , такая, что ;

5. Для случайной величины существует дифференцируемая функция распределения , удовлетворяющая (26);

6. Существует , такая, что для любого ;

7. Существует решение задачи - го этапа , причем

,

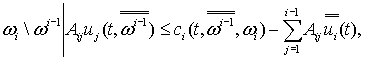где вектора и определяют границы параллелепипеда тогда