Шилинец В. А., Пекарчик Д. И., Хомич И. И.

Белорусский государственный педагогический университет

РЕШЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ФОРМАЛЬНЫХ ПРОИЗВОДНЫХ

В настоящей работе используются бикомплексные функции, моногенные в смысле В.С. Федорова, для построения решений следующей системы дифференциальных уравнений в формальных производных:

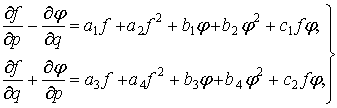                 (1)

где  − известные (искомые) комплексные функции от . Все функции, рассматриваемые в данной работе, предполагаем непрерывно дифференцируемыми функциями действительных переменных  в некоторой односвязной области . Всюду через  обозначаем две такие комплексные функции, для которых  в рассматриваемой области. Операторы  и  определяются следующим образом:

 ,.

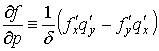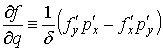Для всякой бикомплексной непрерывно дифференцируемой функции  вводим следующие дифференциальные операторы:

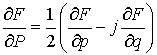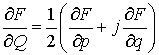,                       (2)

.

Легко доказать, что для этих операторов имеют место обычные правила дифференцирования суммы, произведения и частного. Кроме того имеем:

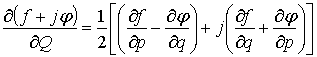.                      (3)

Теорема 1. В случае

                         (4)

                                          (5)

система (1) приводится к виду

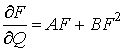,                                        (6)

где

, ,,

.

Доказательство. Из определения дифференциальных операторов (2) и из (1) и (5) следует, что

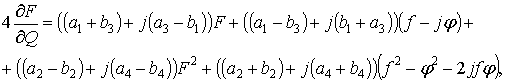
откуда в случае (4) приходим к уравнению (6).

Теорема 1 доказана.

Найдем общее решение уравнения (6), где − неизвестная бикомплексная функция, − известные бикомплексные функции, причем предполагаем, что  и − моногенные в смысле В.С.Фёдорова функции по функции  в области .

Полагаем

.

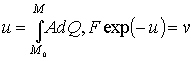При этом имеем: − моногенная в смысле В.С.Фёдорова функция по функции ;

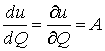,                                              (7)

где − производная в смысле В.С.Фёдорова; .

Уравнение (6) примет вид

,

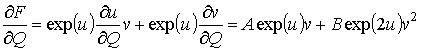откуда и из (7) получим

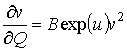.                                       (8)

Полагая , имеем .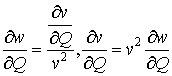

Из (8) получим

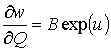.                                             (9)

По определению 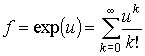, откуда

.

Из последнего равенства имеем: если − функция, моногенная в смысле В.С.Фёдорова по функции , то − также моногенная функция по  в области , причем

.

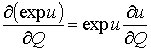Следовательно,  есть функция, моногенная в смысле В.С.Фёдорова по функции  в области .

Из (9) получим

,

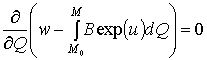т.е.

,

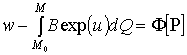где  − моногенная по  в области  функция.

Таким образом,

,

где

, ,

,

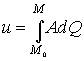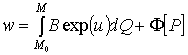 − моногенная в области  по функции  функция.

Замечание. Пусть в уравнении (6)  и − некоторые постоянные. Тогда полагаем

.

Уравнение (6) примет вид

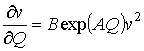.                                      (10)

Полагаем , тогда

.

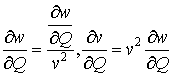Из (10) имеем

,

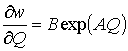откуда

.