Юхименко Б.И., Донченко Ю.Е.

Одесский национальный политехнический университет

Приближенный алгоритм метода ветвей и границ для решения задач целочисленного линейного программирования

Для комбинаторных методов решения задач целочисленного линейного программирования (ЦЛП) характерно использование конечности множества вариантов решения и замена полного перебора вариантов решения частичным. Уменьшение перебора осуществляется отсеиванием неперспективных решений, которые заведомо не являются оптимальными.

Одно из центральных мест среди методов этой группы занимает метод ветвей и границ [1]. Метод применяется для определения максимального значения функции на некотором конечном множестве вариантов решения . Он опирается на следующие построения:

- вычисление верхней границы значения целевой функции либо на множестве , либо на некотором его подмножестве (оценивание);

- постепенное разбиение множества на подмножества (ветвление);

- пересчёт оценок при постепенном разбиении множества;

- нахождение конкретных вариантов;

- проверка вариантов на оптимальность.

Алгоритмы, реализующие метод ветвей и границ, в основном отличаются способами вычисления оценок и ветвления [3].

Известны различные подходы к вычислению оценок[4].

Скорость сходимости алгоритмов непосредственно зависит от процедуры получения оценок и их точности по отношению к значению функции , поскольку признак оптимальности сформирован на оценках.

Увеличение точности получаемых оценок приводит к значительным вычислительным и временным трудностям. Упрощение – к большому перебору получаемых вариантов.

Данная работа навеяна идеями динамического программирования. В какой то степени, через реккурентное соотношение оценивается продолжение некоторого частичного решения [4].По наилучшей оценке определяется оптимальное значение конкретизируемой переменной. Перебор получаемых вариантов не осуществляется, и он заменяется только перебором возможных значений конкретизируемой переменной, среди которых и определяется оптимальное. На каждом шаге конкретизации определяется наилучшее значение конкретизируемой переменной. Шагов конкретизации будет столько, сколько переменных могут иметь положительное значение. Оптимальное решение при таком подходе не гарантируется. Отсутствует явный признак оптимальности. В большинстве случаев получается оптимальное решение, а достаточно близкое к оптимальному решению гарантируется.

Приведенный подход рассматривался для задачи ЦЛП в постановке:

при ограничениях

;

;

.

Введём следующие обозначения:

k - число конкретизированных компонент;

- частичное решение, в котором конкретизировано k компонент;

- множество индексов конкретизированных переменных;

- значение целевой функции для частичного решения ;

- остаток компонент правых частей после определения ;

- множество «хороших векторов» (индексов тех переменных, которые могут принять значение больше ноля), где для всех ;

-величина баллов, оценивающих j – ую переменную, , где определяется по формуле 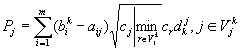, если 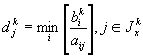, а - целая часть .

Множества и множества максимальных значений не конкретизированных, но принадлежащих множеству «хороших векторов» и их индексов, соответственно упорядоченных в порядке убывания баллов, оценивающих конкретизируемую переменную.

- все частичные решения для конкретизируемой переменной.

Алгоритм решения следующий:

Шаг 1. Положить k=0;.

Шаг 2. Определить множество «хороших векторов». Если множество не пусто, то перейти к шагу 3. Иначе решение получено.

Шаг 3. Определить величины баллов , оценивающих каждую j – ую переменную , и упорядочить их согласно баллам.

Шаг 4. Определить интервал значений для переменной , стоящей первой в ранжированном ряду, то есть .

Шаг 5. Сформировать все частичные решения пока .

Шаг 6. Определить все .

Шаг 7. Определить для всех s.

Шаг 8. Вычислить .

Шаг 9. k=k+1; Перейти к шагу 2.

Эксперимент показал, что разработанный алгоритм сходится довольно быстро. Показатель уровня эффективности (скорости сходимости) рассматриваемого алгоритма намного выше, чем аналогичный показатель сходимости классического алгоритма для метода ветвей и границ.

Приведенный алгоритм был апробирован на решение 100 задач различной размерности, начиная с {m=5,n=10} до {m=20,n=120}. Те же задачи решались точным алгоритмом [4].

Полученное оптимальное решение во многом зависит от степени разброса коэффициентов в системе ограничений, а именно , которые в свою очередь зависят от величины , где

Если значение, которое может принимать колеблется в интервале [- ;+ ], где принадлежит сегменту [0,1], либо больше 15, то алгоритм сходится за наименьшее число шагов. И оптимальное решение представляет собой вектор , где 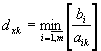.То есть целевая функция достигает максимума в данном случае тогда, когда все переменные задачи за исключением равны нолю, а соответственно принимает значение правой границы сегмента [0,]. Выходит, что алгоритм сходится за одну итерацию, если считать таковой процедуру конкретизации одной переменной.

Если же величина принадлежит [5,15], то алгоритм работает также быстро, как и в случае, описанном выше, но количество итераций увеличивается в соответствии с увеличением размерности задачи.

В заключении следует отметить, что предлагаемый алгоритм работает в 1,5 -2 раза быстрее, кроме того, для 95 задач из 100 был получен оптимальный план.

1. Land A.H. Automatic method of solving discrete programming problems/Land A.H., Doig A.G.//Econometrica.-1960.-vol.28, №3.-p.497-520.

2. Корбут А.А. Метод ветвей и границ (обзор теории, алгоритмов, программ и приложений)/Корбут А.А., Сиган И.Х., Финкельштейн Ю.Ю.//Math. Operatiousforsch.Statist. Ser.Optimization.-1997.-vol.20, №2.-p.253-280.

3. Юхіменко Б.І. Вибір ефективного алгоритму розв’язання задач цілочисленного лінійного програмування//Тр. Одес. политехн. ун-та.- 2003.-Вып.2.-с.172-176.

4. Юхименко Б.И. Ускоренный алгоритм метода ветвей и границ при решении задач целочисленного линейного программирования//Тр. Одес. политехн. ун-та.-2004.-Вып.2.-с.223-226.