ИЗОМОРФИЗМ КЛАССОВ БЕСОВА
НА ДВОИЧНОЙ ГРУППЕ.
Бокаев Нуржан Адилханович, Игенберлина Алуа Еркиновна.
Для классических пространств
Бесова понятия нулевых классов ![]() , изоморфизмы
, изоморфизмы ![]() для разных
для разных ![]() , были установлены в работах Кальдерона, Ароншайна,
Тэйблсона, Никольского. Предложенная в данной работе теорема
дает представление функций класса
, были установлены в работах Кальдерона, Ароншайна,
Тэйблсона, Никольского. Предложенная в данной работе теорема
дает представление функций класса ![]() через свертку ядра
через свертку ядра ![]() с функциями класса
с функциями класса ![]() на двоичной группе.
на двоичной группе.
Классическая
система функций Уолша ![]() на полуинтервале [0,1) определяется следующим образом. Рассмотрим так называемую
систему функций Радемахера
на полуинтервале [0,1) определяется следующим образом. Рассмотрим так называемую
систему функций Радемахера ![]() :
:
![]()
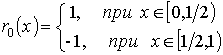 ,
,
![]() -всевозможные сжатия функции
-всевозможные сжатия функции ![]() , продолженной
, продолженной
периодически на всю ось, в ![]() раз. Положим
раз. Положим ![]() Чтобы определить
Чтобы определить ![]() для
для ![]() , представим натуральное число
, представим натуральное число ![]() в двоичном виде
в двоичном виде
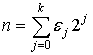 ,
,
где ![]() или 1,
или 1, ![]() . Тогда положим
. Тогда положим
![]() .
.
Полуинтервалы вида:
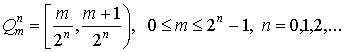
будем называть двоичными интервалами ![]() го ранга. Они задают разбиение полуинтервала
го ранга. Они задают разбиение полуинтервала ![]() :
:
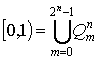 ,
,
при этом ![]() . Произвольный интервал ранга
. Произвольный интервал ранга ![]() обозначим через
обозначим через ![]() .
.
Через 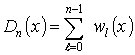 oбозначим
ядро Дирихле по системе
oбозначим
ядро Дирихле по системе ![]() .
.
Пусть![]() . Рассмотрим ряд Фурье-Уолша функции
. Рассмотрим ряд Фурье-Уолша функции ![]()
![]() ~
~ ![]()
где ![]() -коэффициенты Фурье-Уолша.
-коэффициенты Фурье-Уолша.
Прямоугольные
частичные суммы ряда Фурье-Уолша порядка ![]() обозначим:
обозначим:
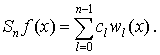
Пусть ![]() - семейство функций
на
- семейство функций
на ![]() таких, что
таких, что
![]() ,
, ![]() ,
,
где![]() - характеристическая
функция множества
- характеристическая
функция множества ![]() .
.
Пусть ![]() .
Через
.
Через ![]() обозначим множество
обозначим множество
функций ![]() для которых
для которых
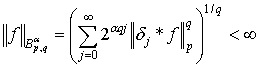 ,
,
где * есть двоичная свертка:
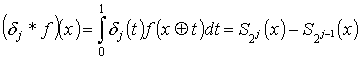 .
.
Такое множество назовем
пространством Бесова на двоичной группе ![]() .
.
Пусть
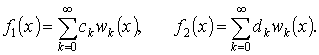
Назовем сверткой двух функций
ряд
![]() .
.
Введем следующий специальный ряд:
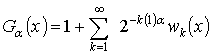 ,
,
где ![]() старший показатель в двоичном разложении
старший показатель в двоичном разложении ![]()
![]() …,
…, ![]() .
.
Рассмотрим оператор
![]()
и ![]() назовем его ядром.
назовем его ядром.
Определение 1. Функция ![]() называется регулярной
в смысле
называется регулярной
в смысле ![]() ,
, ![]() , если для некоторого
, если для некоторого ![]() .
.
Определение 2. Пусть ![]() .
Будем говорить, что
.
Будем говорить, что ![]() принадлежит нулевому
классу
принадлежит нулевому
классу ![]() , если
, если ![]() регулярна в смысле
регулярна в смысле![]() и её ряд Фурье-Уолша таков, что
и её ряд Фурье-Уолша таков, что
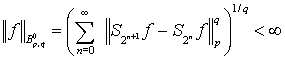 .
.
Теорема. Пусть ![]() . Оператор
. Оператор![]() ,
осуществляет изоморфизм
,
осуществляет изоморфизм
![]() .
.
Доказательство: Пусть![]() , тогда, регулярная в смысле
, тогда, регулярная в смысле ![]() , функция представима в виде:
, функция представима в виде:
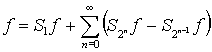 , (1)
, (1)
где
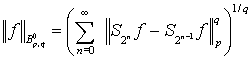 .
.
Докажем, что ![]() . Согласно регулярности в смысле
. Согласно регулярности в смысле ![]() , функция
, функция ![]() разлагается в ряд
разлагается в ряд
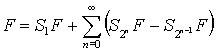 . (2)
. (2)
Из
определения оператора ![]()
![]() .
.
Тогда
![]() .
.
Далее
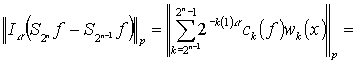
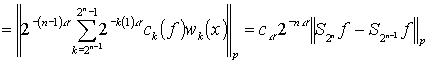 .
.
Следовательно
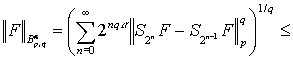
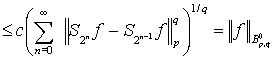 .
.
И обратно, пусть ![]() , для которого верно разложение (2) и
, для которого верно разложение (2) и
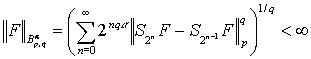 .
.
Для ![]() существует разложение
(1) и
существует разложение
(1) и
![]()
![]() .
.
Следовательно
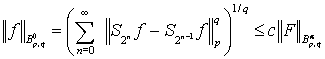 .
.