Федеральное государственное образовательное учреждение
высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

 

Институт градостроительства, управления и региональной экономики

 

 

 

 

 

Кафедра «Информационные технологии»

 

 

 

 

 

 

 

 

РЕШЕНИЕ ЭКОНОМИЧЕСКИХ ЗАДАЧ В «MATHCAD»

Вариант № 18

 

Пояснительная записка к курсовой работе по дисциплине
«Информатика и программирование»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Красноярск 2009

 

 

СОДЕРЖАНИЕ

 

Введение

1.     Постановка задач

2.     Решение задачи № 1

3.     Решение задачи № 2

4.     Решение задачи № 3

Список литературы

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПОСТАНОВКА ЗАДАЧ

 

Задача № 1 (2.17)

Найдите методом наименьших квадратов значения коэффициентов линейной зависимости y=ax+b по заданным эмпирическим данным. Используя найденную линейную зависимость вычислите значение y в точке  x=N + 0.55, где N – номер варианта (N = 18)

x

3

3.1

3.2

3.3

3.4

3.5

3.6

3.7

3.8

3.9

4

y

4.615

4.591

5.13

5.481

5.492

5.553

5.471

5.727

5.798

6.11

6.605

 

Задача № 2 (3.42)

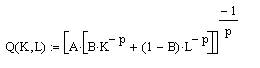Исследуйте поведение заданной CES-функции. Изобразите ее график и изокванты. Вычислите предельную норму замены труда капиталом и эластичность.

Выполните вычисления для CES-функции

где, A = 1.25     B = 0.656      p = 0.67

 

Задача № 3 (4.10)

Постройте графики решения и фазовые портреты динамической си­стемы, моделирующей взаимодействие популяций

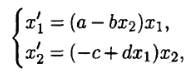
при заданных значениях параметров a, b, c, d.   Исследуйте поведение решения, изменяя параметры: a = 5, b = 3, с = 3, d = 1.

 

 

 

 

 

 

РЕШЕНИЕ ЗАДАЧИ № 1

 

Задание: найдите методом наименьших квадратов значения коэффициентов линейной зависимости y=ax+b по заданным эмпирическим данным. Используя найденную линейную зависимость вычислите значение y в точке  x=N + 0.55, где N – номер варианта (N = 18)

x

3

3.1

3.2

3.3

3.4

3.5

3.6

3.7

3.8

3.9

4

y

4.615

4.591

5.13

5.481

5.492

5.553

5.471

5.727

5.798

6.11

6.605

 

Порядок выполнения задания:

1.  Установить автоматический режим вычислений.

2.  Присвоить переменной ORIGIN значение, равное единице.

3.  Ввести векторы x, y  элементы которых — заданные эмпи­рические данные.

4.  Определить матрицу А соответствующей линейной системы, первый столбец которой А<х> = x а элементы второго — единицы.

5. Найти решение нормальной системы метода наименьших квадратов, используя функцию Isolve.

6.  Вычислить аппроксимирующую прямую, используя функции intersept(x, у) и slope(x.y), которые вычисляют по заданным векторам экспериментальных данных x, у коэффициенты b, а.

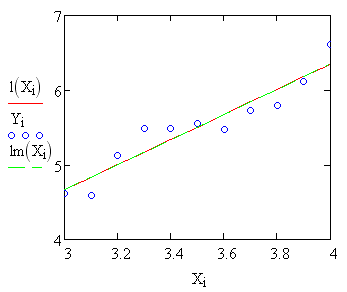
7.  Изобразить графики полученных линейных функций и задан­ные экспериментальные точки.

8.  Найти значение у = ах + b в указанной точке х.

 

Теоретические сведения:

Функция lsolve(A,b) возвращает вектор х решения системы Ах=b, найденного методом Гаусса с оценкой числа обусловленности. Здесь не используется явная формула решения нормальной обобщенной системы х = (АТА)-1АТb, поскольку часто в задачах об аппроксимации эмпирических данных матрица АT А получается плохо обусловленной (матрица А плохо обусловлена, если малые изменения ее элементов (например, округление) приводят к существенным изменениям элементов матрицы A-1. Число обусловленности матрицы cond(A) — мера зависимости погрешностей вычисления А-1 от погрешности элементов А. Например, можно определить число обусловлен­ности как модуль отношения наибольшего собственного значения матрицы к ее наименьшему собственному значению) и при вычислении обратной к ней матрицы возникают большие погрешности округления.

Функции intersept(x, у) и slope(x, у) возвращают значения коэффициентов b и а линейной функции y= х + b, аппроксимирующей экспериментальные данные, сохраненные в векторах х и у.

 

Решение:

1.     Установить режим автоматических вычислений;

2.      ;

3.      

,

 

 

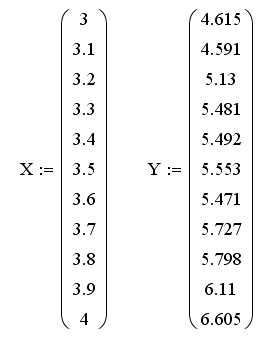
4.      

;

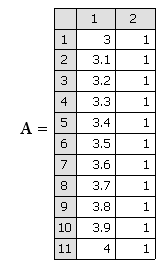5.      

    , ;

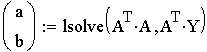6.      ;  

7.       ;

8.      

 

РЕШЕНИЕ ЗАДАЧИ № 2

 

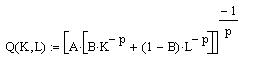Задание: исследуйте поведение заданной CES-функции. Изобразите ее график и изокванты. Вычислите предельную норму замены труда капиталом и эластичность.

Выполните вычисления для CES-функции

где, A = 1.25     B = 0.656      p = 0.67

 

Порядок выполнения задания:

1.  Установить режим автоматических вычислений;

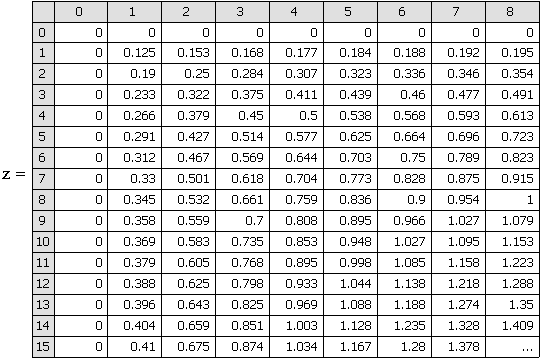
2.  Определить заданную CES-функцию как функцию двух пере­менных К и L;

3.  Определить сетки значений обеих переменных и сформировать матрицу значений в узлах сетки;

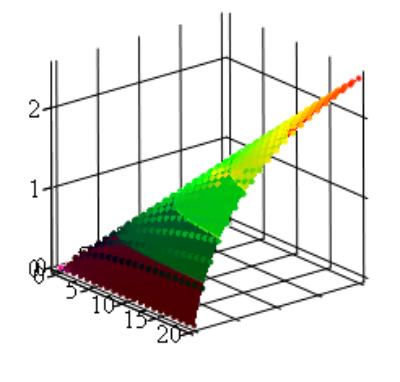
4.  Построить график функции, выбрав в окне параметров гра­фика режим построения поверхности;

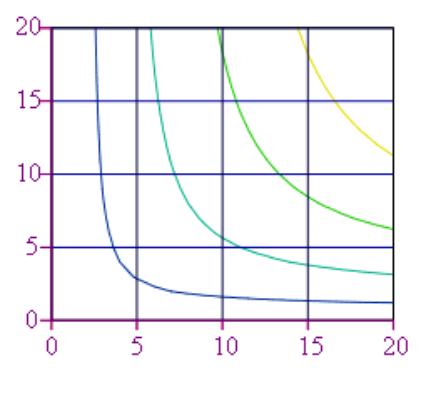
5. Построить линии уровня, выбрав в окне параметров графика режим построения линий уровня;

6. Определить предельную норму замены труда капиталом и ее эластичность.

 

Теоретические сведения:

Рассматриваемая нами CES–функция (CES – Constant Elasticity of Substitution) является производственной функцией с постоянной эластичностью замащения.

Определим же теперь, что будем понимать под производственной функцией.

Производственная функция нескольких переменных описывает зависи­мость объема выпускаемой продукции от затрачиваемых или исполь­зуемых ресурсов, т.е. в записи у = f(x1, x2…xn ) выпуск у единиц продукции определяется объемами  x1, x2…xn затрачиваемых ре­сурсов. Естественно, что областью определения производственной функции (говорят еще: многофакторной производственной функции) является множество x1≥ 0, x2≥ 0…xn≥ 0.  Если производственная функция описывает технологию действую­щего предприятия, то в качестве ресурсов могут фигурировать затра­ты рабочего времени, сырья, комплектующих изделий, энергии, основ­ного капитала. Если производственная функция описывает экономику региона, то в качестве ресурсов обычно рассматривают основной ка­питал, живой труд и природные ресурсы, а значением функции в этом случае обычно является совокупный продукт (доход) региона.

Рассмотрим производственную функцию двух переменных Q=f(K,L), описывающую зависимость выпуска продукции Q от вло­женного капитала К и затраченного труда L. График производственной функции двух переменных — поверх­ность в трехмерном пространстве. Линия уровня производственной функции, т.е. линия, в каждой точке которой объем выпуска при раз­ных значениях К и L один и тот же, называется изоквантой или кривой безразличия производства. Уравнение изокванты имеет вид f(K,L) = const. Изокванты не пересекаются; большему объему производства отве­чают изокванты, более удаленные от начала координат; касательные к изоквантам имеют отрицательный угловой коэффициент.

При исследовании свойств производственной функции используют предельные величины. Предельным продуктом капитала называется предел отношения приращения количества произведенной продукции к вызвавшему это приращение приросту вложенного капитала. Аналогично предельным продуктом труда называется предел от­ношения приращения количества произведенной продукции к вызвав­шему это приращение приросту вложенного труда.

Величина R вычисленная в точках иэокванты, называется коэффициентом заменяемости ресурсов. Он показывает, на сколь­ко единиц нужно увеличить вложение капитала при уменьшении на единицу вложенного труда с тем, чтобы выпуск не изменился. Гео­метрический смысл коэффициента заменяемости ресурсов — угловой коэффициент касательной к изокванте.

 

Решение:

1.   Установить режим автоматических вычислений;

2.   ;

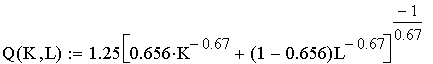3.    

, ;

, ;

;

 

;

 

 

 

 

 

4.   График CES–функции:

 

5.   Изокванта:

 

 

6.    Предельная норма замены труда капиталом:

 

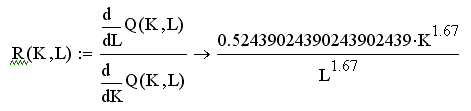
Эластичность:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РЕШЕНИЕ ЗАДАЧИ № 3

 

Задание: постройте графики решения и фазовые портреты динамической си­стемы, моделирующей взаимодействие популяций

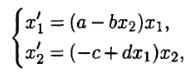
при заданных значениях параметров a, b, c, d.   Исследуйте поведение решения, изменяя параметры: a = 5, b = 3, с = 3, d = 1.

 

Порядок выполнения задания:

1.   Установить режим автоматических вычислений;

2.   Присвоить переменной ORIGIN значение, равное единице;

3.   Определить вектор–столбец начальных условий для первой задачи Коши;

4.   Определить вектор-столбец правых частей системы;

5.   Решить задачу Коши для первого начального условия.

6.   Определить векторы–столбцы остальных начальных условий для каждого начального условия и решить задачу Коши для каждого из условий;

7.   Изобразить  соответствующие  фазовые портреты и графики решения.

 

Теоретические сведения:

В динамике популяций есть много примеров, когда изменение числен­ности популяций во времени носит колебательный характер. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтерра — Лотка.

Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества. Пусть x1 и x2 — число жертв и хищников соответственно. Предположим, что относительный прирост жертв  равен a — bx2,  a, b > 0, где а — скорость размножения жертв в отсутствие хищников, —bx2 — потери от хищников. Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи (x1 = 0) относительная скорость изменения по­пуляции хищников равна                         наличие пищи компенсирует убывание, и при х1 > 0 имеем  

 

Решение:

1.   Установить режим автоматических вычислений;

2.      ;

3.    

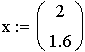
4.    

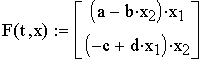
5.    

, сохраняем в матрице Х1 решение, вычисленное методом Рунге – Кутты с постоянным шагом на отрезке [0, 10] в 400 точках, первый столбец этой матрицы содержит значение аргумента t – координаты 400 узлов сетки, второй столбец – значения х1 (число жертв) в узлах сетки, а третий – значения х2 (число хищников).

6.    

, ;

, ;

, .

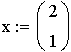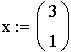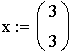7.    

График первого решения:

 

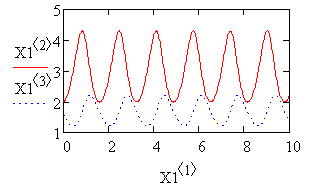
График второго решения:

 

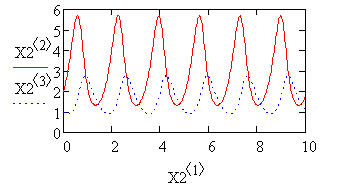
График третьего решения:

 

 

 

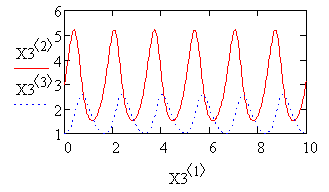
График четвертого решения:

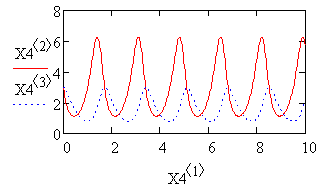
Фазовые портреты:

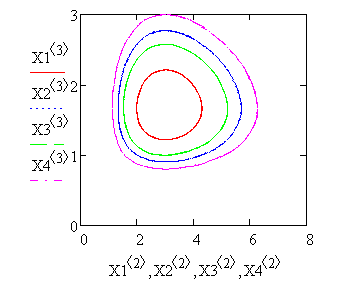
Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3:1 (Х3) обе популяции сначала растут, когда число хищников достигает величины 2,5, популяция жертв не успевает восстанавливаться и число жертв начинает убывать. Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников, и, когда число жертв достигает величины 2 число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины 1,6. С этого момента начинает расти популяция жертв; через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и процесс повторяется снова и снова. На графике четко виден периодический характер процесса.

Отметим, что рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и др.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ЛИТЕРАТУРЫ

 

1.   Дьяконов В.П. Справочник по MathCad 7.0 Pro. – M: СК Пресс, 1998.

2.   Плис А.И. MathCad: математический практикум для экономистов и инженеров / А.И. Плис, Н.А. Сливина. М. «Финансы и статистика», 1999.

3.   Солодовников А.С. Математика в экономике. – М.: Фининсы и статистика, 1998.