Математика/
Дифференциальные и интегральные уравнения
К.ф.-м.н. Карнишин С.Г., Карнишиа В.И.
Пермский военный институт внутренних войск МВД России
(ПВИ ВВ МВД России), МБОУ «СОШ № 47», г.Пермь, Россия
Задача о
допустимости пар пространств с векторным весом
Рассмотрим линейное
функционально-дифференциальное уравнение
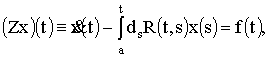
![]() (1)
(1)
Предполагаются выполненными следующие
условия: элементы ![]()
![]() - матрицы
- матрицы ![]() определены в области
определены в области ![]() ; функции
; функции ![]() при каждом
фиксированном
при каждом
фиксированном ![]() суммируемы на каждом
конечном отрезке из
суммируемы на каждом
конечном отрезке из ![]() , полные вариации
, полные вариации ![]() и компоненты
вектор-функции
и компоненты
вектор-функции ![]() суммируемы на каждом
конечном отрезке из
суммируемы на каждом
конечном отрезке из ![]()
![]()
Всюду в дальнейшем через ![]() будем обозначать
будем обозначать ![]() -мерное векторное пространство, через
-мерное векторное пространство, через ![]() - норму
- норму ![]() .
.
Введём следующие специальные пространства
функций со значениями в ![]() . Пусть
. Пусть ![]() , - скалярные непрерывные положительные на
, - скалярные непрерывные положительные на ![]() функции.
функции.
1.
Пространство ![]() определим как пространство непрерывных вектор-функций
определим как пространство непрерывных вектор-функций ![]() для которых
произведения
для которых
произведения ![]()
![]() ,
, ![]() ограничены на
ограничены на ![]() . Норму в
. Норму в ![]() определим равенством
определим равенством
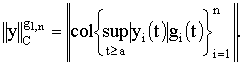
2.
Обозначим через ![]() пространство
вектор-функций
пространство
вектор-функций ![]() для которых
произведения
для которых
произведения ![]() ,
, ![]() ограничены в существенном
на
ограничены в существенном
на ![]() .
Норму в пространстве
.
Норму в пространстве ![]() определим равенством
определим равенством
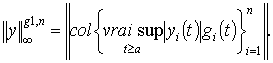
3.
Пусть ![]() ,
, ![]() . Через
. Через ![]() обозначим
пространство вектор-функций
обозначим
пространство вектор-функций ![]() для которых произведения
для которых произведения
![]() суммируемы на
суммируемы на ![]() в степени
в степени ![]() ,
, ![]() . Норму в пространстве
. Норму в пространстве ![]() определим равенством
определим равенством
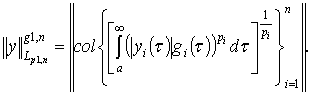
4.
Через ![]() обозначим
пространство вектор-функций
обозначим
пространство вектор-функций ![]() для которых интегралы
для которых интегралы
![]() существуют и равномерно ограничены по
существуют и равномерно ограничены по ![]() на
на ![]() . Норму в пространстве
. Норму в пространстве ![]() зададим равенством
зададим равенством
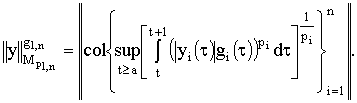
Рассмотрим для уравнения (1) задачу Коши
![]() ;
; ![]() . (2)
. (2)
Хорошо известно, что любое решение уравнения
(1) имеет представление
![]() ,
,
где ![]() - матрица Коши
уравнения (1). Из этого представления видно, что свойства устойчивости по части
переменных полностью определяются свойствами фундаментальной матрицы
- матрица Коши
уравнения (1). Из этого представления видно, что свойства устойчивости по части
переменных полностью определяются свойствами фундаментальной матрицы ![]() . А именно решение задачи (2) устойчиво по первым
. А именно решение задачи (2) устойчиво по первым ![]() переменным тогда и только тогда, когда
переменным тогда и только тогда, когда ![]()
Обозначим через ![]() столбцы
фундаментальной матрицы. Из сказанного выше очевидно следует, что если
столбцы
фундаментальной матрицы. Из сказанного выше очевидно следует, что если ![]() , где
, где ![]() , то решение задачи (2) устойчиво по первым
, то решение задачи (2) устойчиво по первым ![]() компонентам.
компонентам.
Пусть ![]() - банаховы
пространства измеримых вектор-функций, определённых на
- банаховы
пространства измеримых вектор-функций, определённых на ![]() .
.
Определение
1. Будем говорить, что для уравнения
(1) допустима пара ![]() , если каждому
, если каждому ![]() соответствует решение
соответствует решение
![]() задачи (2) при
задачи (2) при ![]() ,
принадлежащее
,
принадлежащее ![]() .
.
Для фундаментальной матрицы ![]() уравнение (1) известно
следующее представление:
уравнение (1) известно
следующее представление:
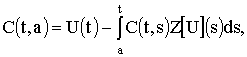
где ![]() -
- ![]() - матрица с абсолютно
непрерывными на
- матрица с абсолютно
непрерывными на ![]() компонентами,
удовлетворяющая условию
компонентами,
удовлетворяющая условию ![]() ,
, ![]() - единичная матрица.
- единичная матрица.
Лемма
1. Пусть выполнены условия:
1)
для уравнения (1)
допустима пара ![]() ;
;
2)
столбцы матрицы ![]() принадлежат
пространству
принадлежат
пространству ![]() ;
;
3)
столбцы матрицы ![]() принадлежат
пространству
принадлежат
пространству ![]() ;
;
Тогда ![]() .
.
Из этой леммы видна связь между задачей о
допустимости пары ![]() и устойчивости по
части переменных решений уравнения (1).
и устойчивости по
части переменных решений уравнения (1).
Сформулируем критерии разрешимости задачи
о допустимости пар пространств для уравнения (1) в случае пространств с
векторным весом. Предварительно введем следующие понятия.
Определение
2. Будем говорить, что для матрицы ![]() выполнено
выполнено ![]() -условие, если существует такая постоянная
-условие, если существует такая постоянная ![]() , что
, что ![]() при
при ![]() .
.
Обозначим
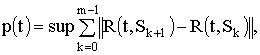
где верхняя грань берётся по всевозможным разбиениям ![]() отрезка
отрезка ![]() .
.
Теорема
1. Пусть матрица ![]() удовлетворяет
удовлетворяет ![]() -условию и
-условию и ![]() ,
, ![]() . Пусть далее функции
. Пусть далее функции ![]() и
и ![]() ,
, ![]() удовлетворяют
условию: существует положительная постоянная
удовлетворяют
условию: существует положительная постоянная ![]() , такая, что при любых
, такая, что при любых ![]() выполняется
неравенство
выполняется
неравенство ![]() ,
, ![]() . Следующие утверждения эквивалентны:
. Следующие утверждения эквивалентны:
а) для решения (1) допустима пара![]() ;
;
б) существует такое ![]() , что при
, что при ![]() и
и ![]() для уравнения (1)
допустима пара
для уравнения (1)
допустима пара ![]() ;
;
в) существует положительная переменная ![]() , такая, что элементы матрицы Коши уравнения (1)
удовлетворяют оценке
, такая, что элементы матрицы Коши уравнения (1)
удовлетворяют оценке
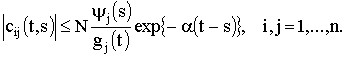 (3)
(3)
Теорема
2. Пусть выполнены условия теоремы 1
и, кроме того, функции ![]() ,
, ![]() , удовлетворяет условию: существует положительная постоянная
, удовлетворяет условию: существует положительная постоянная ![]() , такая, что
, такая, что ![]() ,
, ![]() . Следующие утверждения эквивалентны:
. Следующие утверждения эквивалентны:
а) для уравнения (1) допустима пара ![]() ;
;
б) для уравнения (1) допустима пара ![]() ;
; ![]() ;
;
в) для уравнения (1) допустима пара ![]()
![]() ;
; ![]() ;
;
г) существуют положительные ![]() и
и ![]() , такие, что элементы матрицы Коши уравнения (1)
удовлетворяют оценке (3).
, такие, что элементы матрицы Коши уравнения (1)
удовлетворяют оценке (3).
Литература
1. Азбелев
Н.В., Березанский Л.М., Симонов П.М., Чистяков А.В. Устойчивость линейных
систем с последствием. 1. Дифференц. уравнения. 1987. Т.23. № 5. С.745-754.
2. Тышкевич
В.А. Некоторые вопросы теории устойчивости функционально-дифференциальных
уравнений. Киев: Наукова думка, 1981. 80с.