Математика/ 4.Прикладная математика

УДК 378.016.026.7:51(574)

Профессор Abudisha Abudul

Қытай халық Республикасы, Іле Педагогика институты

П.ғ.к., профессор Kurmangali I. Kanlybaev

 Қазақстан Республикасы, Абай атындағы

Қазақ ұлттық педагогикалық университеті

 

ГЕОМЕТРИЯ ЕСЕПТЕРІН ШЕШУ ІЗДЕНІСТЕРІ

 

Қысқаша мазмұны: Геометриялық есептерді шешу барысында оның шартын өзгерту арқылы әртүрлі зерттеу жұмысын жүргізуге болады. Есеп шартында қолданылмаған информацияны зерттеп, ойымызды дамытатын басқа да есептер құрастыруға болады. Мұндай зерттеуге келтірілетін есептер жазықтықтағы салу және кеңістіктегі салулар болып табылады. Жазықтықтағы салулар белгілі аспаптардың көмегімен салынатын болса, кеңістікте мұндай салу аспаптары жоқ, тек аксиомалардың көмегімен салу, түрлендіру, есептері күрделі қатынастарды есептеуге берілген есептер зерттеудің қайнар көзі.

Түйін сөз: «геометрия есебі», «зерттеу», «есеп шартындағы қосымша мәліметтер.

 

Геометрия есептері әр түрлі ізденістерімен жаңалықтар ашуға итермелейді. Кез-келген геометриялық есепті шешу кезінде соған сәйкес геометриялық фигураның әр алуан касиеттері анықталады. Бұл қасиеттер ең болмағанда есептің сұрағына жауап беруге қажетті және жеткілікті болады. Жалпы алғанда есепті шешу кезіндс оған қолданылмайтын басы артық қасиеттерде кездесуі мүмкін. Әр түрлі көзқарас тұрғысынан алғанда маңызды болып табылатын, есеп шартында көрсетілмеген геометриялық фигураның қасиеттерін іздеген кезде ғана геометриялық есептерді зерттеу басталады. Мұндай зерттеу осы есептің шешілуімен тікелей байланысты. Есепті зерттеу барысында фигураның әр түрлі қызықты қасиеттерін іздеумен шектелуге болады. Геометриялық фигурадан табылған жаңа касиеттерді берілген есептің басқа жаңа шешімдерін іздеуге, жаңа есептер құрастыруға болады. Біз бұлшағын зерттеу жұмысында геометрия есептерін зерттеп ондағы есеп шартында көрсетілмеген, осы ссепке қатысты басқа зерттеулерді іздей отырып, табылған қасиеттерді пайдаланып, жаңа есептер құрастырдык, есептердің шартын өзгертіп, оны жалпылал олардағы ортақ қасисттерді көрсеттік. Есептерді әртүрлі мағынада жалпыладық. Ең болмағанда кейбір есептердін шартын түрлендірдік. Ал шешу тәсіліндс оның нәтижесі (әдетте кейбір бұрыштың шамасы) өзгеріссіз қалады. Басқа жағдайларда есеп шарты. есептің қорытындысы өзгертіледі. Дербес жағдайларды жалпылағанда кейде Менелай және Чева теоремалары қолданылды. Бұл есептерді шешу барысында есептерді қосымша зерттеуге басты назар аудардық. Осындай қосымша зерттеудің нәтижесінде мектеп оқушылары жаңа фактілерді үйреніп есепті жалпылау үшін оның шарты мен қорытындысын ұқыпты түрде талдауы мүмкін. Геометрияның мектептегі курсы оқушыларды математикалық тұжырымдарды жалпылай білу дағдысын үйретеді. Бұл мектеп оқушысының теориялық тұрғыда ойлауна, нақты және жалпы білім сапасының артуына мүмкіндік береді. В.А.Крутецский[1]математикалық материалды жалпылаудың әр түрлі екі жолын көрсетті: көп бейнелі кейбір дербес жалпылаудың басқа да жолдары бар. Оқу процесінде шәкірттер берілген оқу материалына сәйкестендірмей, салыстырмай, арнаулы жаттығуларсыз, мүғалімнің көрсетуінсіз өзбетінше математикалық объектілерді, қатыстармен амалдарды талдау арқылы бір құбылыспен қатар оған үқсас құбылысты жалпылауды іске асырады. Жалпылаудың бірінші жолы — нақты-эмприкалық ойлау мүмкіндігі, екінші жолы - ғылыми-теориялык ойлауды дамыту. Біз бұл мақалада жалпылаудың келесі түрлерін қарастырдық[2].

/. Бір есепті не теореманы қарастыру негізінде

 

а)дәлелдеу мен есеп шеіиімін тікелей үйрену;

әі) есепті қайта тұжырымдау арқылы жалпылау.

2. Мұгалім ұсынган бірнеше дербес жағдайларды \үйрену арқылы жалпылау.

3.Жалпы твареманың дербес жагдайларын табу жәнв оны басқа багыгк-па жалпылау.

4.Есептерді талдау мен шешугенегізделіп берілгендерге керісіншеалынған мәліметтер бойынша есептер құрастыру.

Осы айтылған жалпылауларға сүйеніп кұрастырылған есептер окушы білімін тереңдстіп, өзбетінше танымдық әрекетінің сапасын көтереді. Біз есептер шешу барысында сырттай сызылған шеңберді келесі қасиеттерін пайдаландық.

1-теорема. Егер О-АВС шеңберінің центрі, О және В нүктелері АС түзуінің бір жағында жатса, онда  ﮮ АВС =2ﮮ АВС

 

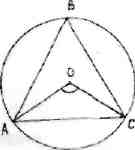1-сурет

2-теорема. ЕгерﮮАВС =2ﮮАВС, | ОА| = |ОС| және О, В нүктелері АС кесіндісінің бір жағында жатса, онда О нүктесі АВС шеңберінің центрі.

3-теорема. Егер АВСД төртбүрышында ﮮА + ﮮС = ﮮВ+ \Dболса, онда ол іштей сызылған.

1-есеп. Берілген квадратка іштей дұрыс үшбұрыш сыз. Бұл есептің шешілуінің әр түрлі жолы белгілі. Мысалы, бұру әдісі, ұқсастык әдісі. Талдау барысында квадрат қабырғасының кез-келген нүктесі оны іштей сызылған дұрыс үшбұрышының төбесі болатынын оңай байқауға болады. Есептің шектеусіз көп шешімі бар. Талдау ретінде мынандай мәселені қарастыруға болады;

Квадратқа іштей сызылған дұрыс үшбұрыштар центрі қандай фигура құрайды? [3].

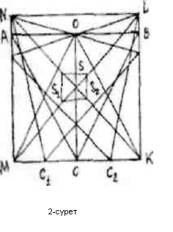
Шешуі: MNLK квадрат берілсін (2-сурет). Алдын-ала АMN, B, CMK болатындай АВС дұрыс үшбұрышын қарастыралық. Егер СО┴АВ, О болса, онда   МАОС   және  СОВК   төртбұрыштары   іштей   сызылған,   сондықтан

ﮮОМС = ﮮОАС = 60, ﮮОКС =ﮮОВС = 600. Бұдан МОК үшбұрышы — дұрыс үшбұрыш деген қорытындыға келеміз. О осы үшбұрыштың төбесі — бұл қарастырылатын барлық үшбұрыштардың (АВ-ның ортасы). АВС үшбұрышының центрінS арқылы белгілсйік. Онда, А нүктесі МN қабырғасы бойынша орын ауыстырғанда, В нүктесі LК квадрат қабырғасы бойынша орын ауыстырады.Онда МК бойында жатқан С нүктесі С1С2 кесіндісінің бойымен қозғалады. Егер А нүктесі N1, де, ОС ┴ОN болса, онда С нүктесімен С1 беттсседі. Егер В=L бірдей болса,   ОС2ЮІ   болса,  онда С  мен С   бірдей.   Бұлжағдайда Sнүктесі [S1S2]=

Есеп шартын қанағаттандыратын кез-келген үшбұрышты қарастырылған АВС үшбұрышын квадраттың центрінен 90°, 180°, 270°-қа бұрып шығарып алуға болады. Сондықтан барлық іштей сызылған дұрыс үшбұрыштар центрлері кабырғасының ұзындығы S1S2квадратын құрайды. Бұл квадраттың центірі берілген квадраттың центрімен беттеседі. АВ қабырғасынын ортасының қасиеті байқалған жаңа қасиет — бұл арқылы жаңа нәтижелерге қол жсекізуге болады. Ең алдымен О нүктесінің көмегімен  АВС үшбұрышын    оңай құрады. (О нүктесі квадрат ішінде жатыр) О нүктесі арқылы MN мен LK-ны қиятын кез-келген түзу жүргіземіз. Ол А, В нүктелеріңде қиылысады.

ОС┴АВ, СMК, ∆АВС — есеп шартын қанағаттандырады. Козғалмайтын О нүктесі МАВК трапециясының өте маңызды жаңа қасиетін байқауға мүмкіндікбереді. |МА| + |КВ| = 2|0С|

(Арақашықтықтар қосындысы О нүктесінен МК дейінгі қашықтықтың екі еселенген көбейтіндісіне тең). Сондықтан іштей сызылған ұшбүрыштың АВ қабырғасын қай жерден таңдап алуға байланысты емес. МАВК трапецияның ауданы тұрақты болады. Бұл арада квадраты МК түзуі және MN, KL екі жарты түзуі арқылы өрнектеуге болады. MN, KLжарты түзулер МК бір жағында жәнебүлар МК-ға ┴болуы керек. Дұрыс АВС үшбұрышы АMN, B, CMK орналасуы керек. АВ-ның ортасы О ұшбұрыштар үшін ортақ. Сондықтан МАВК төртбұрышының ауданы АВ қабыргасын таңдап алуга тәуелсіз. Осы есепке сүйеніп жаңа есеп құрастыруға болады.

2-есеп. Теңбүйірлі үшбұрышты сырттай сызылған шеңбердің ұзындығы 20π-ге тең. Егер үшбұрыш табаны 12 болса, онда осы үшбұрыштың ауданын табыңдар[4].

 

 

 

 

 

 



 

Шешуі: Шеңбер радиусы 10 екені белгілі. Берілген шеңберге табаны ортақ екі теңбүйірлі үшбұрыш салуға болатыны белгілі (3-сурет). Бірінші үшбұрышта С1 –сүйір, екінші үшбұрышта  С2 –доғал.

1-жағдай. FD=2R, мұндағы R-шеңбер радиусы. Бұл арадан =. С1-сүйір болғандықтан, =. Косинустар теоремасы бойынша , бұдан ∆AC1B-ның ауданы S=

2-жағдай. Бұл арада  , бірақ  себебі  -доғал бұрыш.∆AC2B  –ның ауданы 12. Жауабы 108 немсе 12.

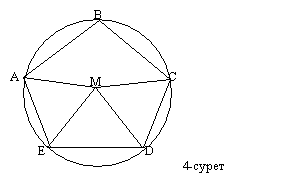
3-есеп. ABCDE–дұрыс бесбұрыш берілген. Ондағы M нүктесі  -∆DEN-теңқабырғалы үшбұрыш болатындай етіп алынған. ∆ANC–ның бұрыштарының шамасын табыңдар.

 

Шешуі: Дұрыс бесбұрыштың ішкі бұрышы 1080 болғандықтан,ﮮОМС = ﮮNDC =  ﮮEDC-ﮮEDN = 1080-600=480 (4-сурет).

 

 

 

 

 

 



∆NDCТеңбүйірлі болғандықтан (ND=DC),ﮮDMC =  (1800 - 480)=660. Дәл осылайша ﮮENA=660 екенін анықтаймыз. Бұл араданﮮANC = 3600  - (600+660+660)=1680. Алайда келтірілген есептің шешуі толық емес. Шынында да есеп шартына N нүктесі дұрыс бесбұрыштың ішінде жатады деп айтылмаған. Сондықтан бұл есептің басқа шешу жолы болуы мүмкін (5-сурет).

 

 

 

 

 

 

 

 

 

 



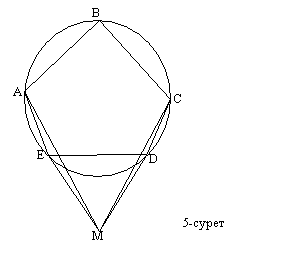
ﮮNDC =  ﮮNDE+ﮮEDC =600+1080=1680. ∆NDC теңбүйірлі (ND=DC) болғандықтан, ﮮCND = 60. Демек, ﮮANC =  ﮮEND-2ﮮCND =600-120=480.

Жауабы 1680 немсе 480.

Қорытынды: Геометрия есептерінің шарттарын қалағанымызша өзгерту арқылы арнайы зерттеу жұмысын жүргізуге болады. Геометрия есептері -  зерттеу жүргізудің негізі.

 

Әдебиеттер:

1.   В.А.Крутецский, Психология математической способности школьников: Книга для учителя.-М:Педагогика.1968.-180б.

2.   Мұқанов М. Ақыл-ой өрісі. Алматы:Қазақстан, 1980.-172б.

3.   Қ.И.Қаңлыбаев. «Геометриялық  түрлендірулер».Алматы:РБК.2001.

4.   Полонский В.Б., Рабинович Е.М., Якир М.С.  Учимся решать задачи по геометрии. Учебно-методическое пособие.-К.: «Магистр», 1996.-256б.