Построение периодического решения для инерционной передачи

с рычажным механизмом

Трансформация момента в инерционных передачах без механизмов свободного хода возможна в случае, когда момент сопротивления на выходном валу импульсного механизма меняет знак в течение цикла [1]. Поставим вопрос: меняет ли знак момент сопротивления при действии на ползун односторонней силы сопротивления в инерционной передаче c рычажным механизмом [2]? Вопрос является важным, потому что положительное его решение позволило бы надеяться на значительное расширение области возможного применения предложенных передач, так как на рабочие органы многих современных машин и механизмов действует одностороннее рабочее сопротивление.

С помощью выражения для элементарной работы получим выражение для момента сопротивления на выходном валу импульсного механизма от действия силы [2]:

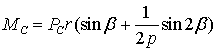. (1)

Пусть составляющая силы сопротивления равна нулю. В этом случае режим заторможенного выходного вала импульсного механизма возможен лишь при . В противном случае, ползун имеет возможность без сопротивления двигаться до тех пор, пока не займет крайнее положение, для которого . Согласно (1), при . Также и по точному выражению 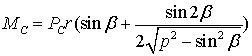получим при .

Учитывая непрерывность функции , запишем

,             (2)

где ,  ─ множество значений, принимаемых углом поворота за цикл установившегося режима работы передачи.

Основываясь на результатах экспериментальных исследований, естественно считать, что цикл работы передачи определяется одним полным оборотом грузовых звеньев в относительном движении. Нетрудно найти выражение для времени цикла установившегося движения

.

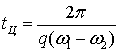Для случая получим

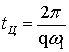. (3)

Как следует из выражения (3), частота колебаний выходных звеньев передачи является постоянной величиной. С учетом условия (2), запишем

,             (4)

где 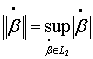,  ─ множество значений, принимаемых угловой скоростью за цикл установившегося режима работы передачи.

Обозначив , условия (2) и (4) объединим в одно

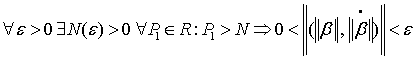,  (5)

где .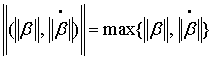

То есть, всегда можно подобрать значение односторонней составляющей силы сопротивления так, что выходной вал импульсного механизма будет совершать колебания, характеризующимися сколь угодно малыми нормами и .

Нас интересует принципиальная возможность действия знакопеременного момента сопротивления при одностороннем сопротивлении , поэтому можно сделать упрощение, положив . При сделанном упрощении и при отсутствии упругого элемента движение передачи можно описать уравнением [2]

. (6)

Функции и представим в виде степенных рядов. Ограничиваясь в разложениях и первым членом ввиду малости угла , получим

.

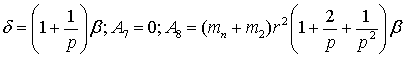Уравнение (6) преобразуем с принятыми допущениями и сделанными преобразованиями

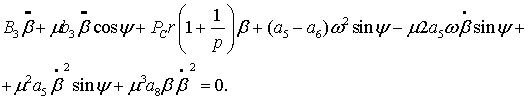(7)

В уравнении (7) ─ параметр, вводимый при малых членах.

При уравнение (7) обращается в уравнение (6).

Функции и разложим в ряды вида

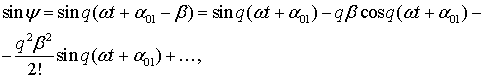(8)

где ─ значение угла в момент времени

В силу быстрой сходимости рядов (8), сохраним в разложениях и только первый член.

Из условия (5) следует, что всегда можно подобрать такое значение , при котором слагаемые в уравнении (7), содержащие параметр , будут сколь угодно малы. Третье слагаемое этого уравнения, несмотря на то, что включает сомножителем малый угол , может оказаться значительным, так как для обеспечения колебаний с малой амплитудой может потребоваться большое значение силы сопротивления .

Уравнение (7) является существенно нелинейным, так как содержит кусочно-линейную функцию . Поэтому интегрирование этого уравнения проведем по участкам с помощью малого параметра. Согласно основной идее этого метода [3], решение уравнения (7) будем искать в виде ряда по степеням параметра :

. (9)

Участок 1:  .

Отбрасывая в уравнении (7) члены, содержащие параметр , получим порождающее уравнение

,

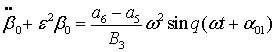в котором .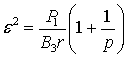

Решение порождающего уравнения имеет вид

,

здесь .

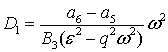Используя начальные условия , находим постоянные интегрирования и :

.

Уравнение для получаем, оставляя в уравнении (7) слагаемые, содержащие параметр в первой степени:

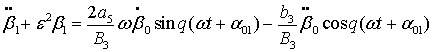. (10)

Интегрируя уравнение (10), находим:

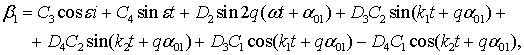
где

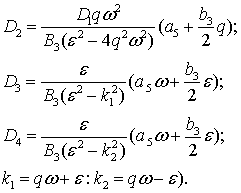
Постоянные и определим при нулевых начальных условиях:

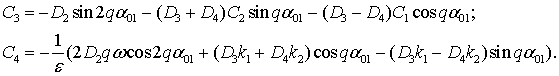
Сохраняя в разложении (9) два первых члена, запишем решение для угла поворота на первом участке

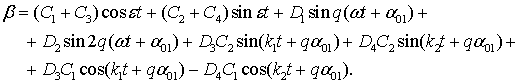(11)

Проверка найденного аналитического решения (11) численными методами показала приемлемость аналитического решения для инженерных расчетов.

Участок 2: .

Аналогично, как и для первого участка, найдем выражение для угла на втором участке:

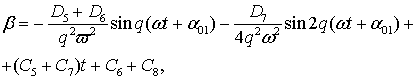(12)

где

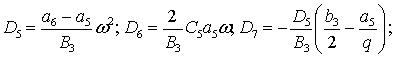
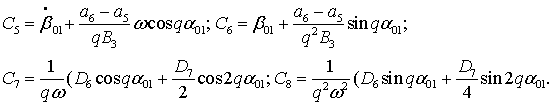
Участок 3: .

Рассмотрим лишь случай, когда , поскольку в любом другом случае время протекания третьего участка равно нулю.

Подставляя нулевые значения производных и в уравнение (6), после небольших преобразований получим:

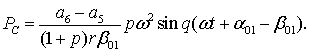(13)

Для построения периодического решения используем метод припасовывания найденных решений посредством согласования значений координаты и скорости на границах участков.

Пусть ─ номера рассмотренных участков, причем среди чисел могут быть и равные. Тогда вектор с составляющими определит тип периодического решения, то есть последовательность участков, описывающих установившийся процесс в течение цикла.

При практическом применении метода припасовывания необходимо задаться предполагаемым типом искомого периодического режима. В большей части случаев задача о выборе типа периодического режима решается интуитивно, причем обычно ограничиваются отысканием периодических режимов простых типов. Основываясь на физических соображениях, будем считать, что для исследуемого установившегося процесса .

Задавшись типом периодического режима и имея решения уравнения (6) по участкам, мы можем свести задачу определения искомого периодического движения к решению системы трансцендентных уравнений с числом уравнений, равным числу неизвестных начальных условий и временных моментов переключения. С другой стороны, периодическое движение можно определить по движению изображающей точки в фазовом пространстве, последовательно просчитывая несколько циклов до тех пор, пока значения координат и скоростей в начале и конце цикла не совпадут с заданной погрешностью. При этом изображающая точка выходит на замкнутую траекторию, соответствующую периодическому движению.

Исследуемая динамическая система, как система с угловыми координатами, имеет цилиндрическое фазовое пространство.

Поверхности переключения в нашем случае представляют собой плоскости, уравнения которых определяются решением уравнения :

Обычно с целью уменьшения углов давления принимают , поэтому .

Плоскости переключения делят развертку цилиндрической поверхности на четыре области. Третий участок определяет скользящие движения системы по плоскости переключения .

Построим, например, периодическое решение уравнения (6) в отсутствие упругого звена для инерционной передачи с параметрами:

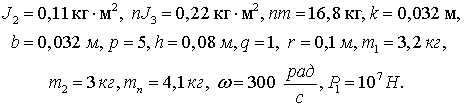(14)

Проекция траектории изображающей точки на координатную плоскость для этой передачи представлена на рис.1. Утолщенной линией изображена проекция предельного цикла, указывающего на существование периодического движения.

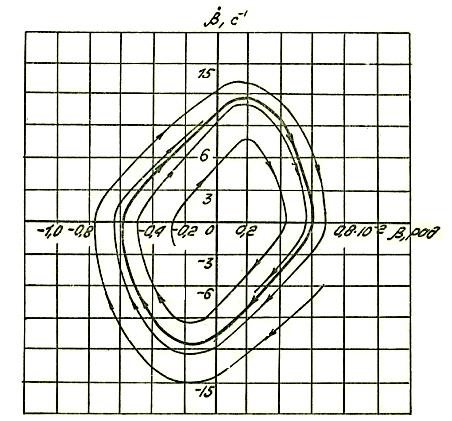
Рис.1. Проекция траектории изображающей точки

Различия между аналитическим и численным решением на диаграмме не прослеживается. Как видно из рис.1, предельный цикл является устойчивым и, следовательно, предельный цикл является устойчивым и, следовательно, отвечает автоколебанию динамической системы.

Время цикла, подсчитанное по формуле (3) и вычисленное с помощью суммирования моментов переключения по участкам, составляет соответственно 0,0209439 с и 0,0209436 с. Высокая сходимость результатов косвенно позволяет судить о правильности аналитических расчетов.

Для предельного цикла построены графики зависимостей от времени (рис.2,3,4). Различия между аналитическими и численными решениями на графиках не прослеживаются.

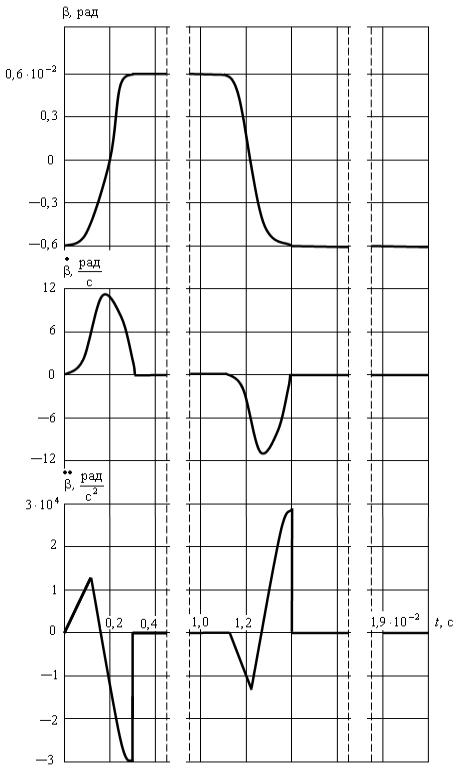
Рис.2. Графики зависимостей угла поворота, скорости и ускорения

выходного вала импульсного механизма от времени

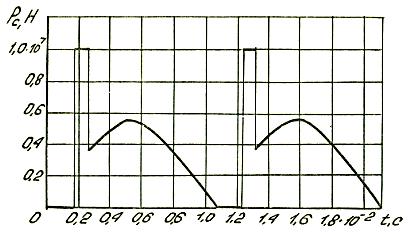
Рис.3. Зависимость силы сопротивления от времени

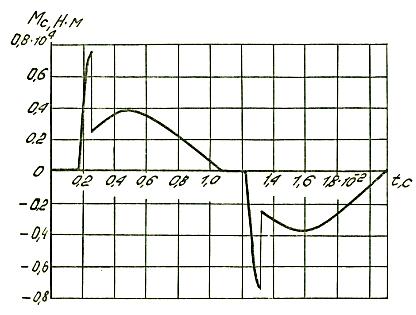
Рис.4. Зависимость момента сопротивления от времени

Анализ графиков (рис.3 и 4) показывает, что для инерционной передачи с рычажным механизмом существуют периодические решения, которые являются устойчивыми, и для которых момент сопротивления на выходном валу меняет знак в течение цикла при действии односторонней силы внешнего сопротивления. Аналогичные расчеты показывают, что смена знака момента сопротивления при одностороннем внешнем сопротивлении возможна и в инерционных передачах без механизмов свободного хода, выполненных и по другим схемам предложенного семейства. Смена знака момента сопротивления на выходном валу импульсного механизма позволяет сделать важный вывод о принципиальной способности инерционных передач предложенного семейства трансформировать момент при действии одностороннего сопротивления на рабочем органе. Сделанный вывод позволяет значительно расширить область применения предложенных инерционных передач без механизмов свободного хода, но с рычажным или эксцентриковым механизмом на выходе. Кроме того, этот вывод, наряду с тем, что позволяет расширить область применения передач, также является и основой для создания инерционных передач лишь с одним выходным механизмом свободного хода.

Литература:

1. Леонов А.И. Инерционные автоматические трансформаторы вращающего момента. М.: Машиностроение, 1978. 224 с.

2. Алюков С.В. Динамика инерционного трансформатора вращающего момента без механизмов свободного хода: Автореф. дис. …канд. техн. наук, ВПИ, 1983.

3. Алюков С.В. Сравнительный анализ приближенных методов решения дифференциальных уравнений движения инерционно-импульсных передач // Вестник машиностроения, Москва, 2010, №6, C. 3─10.