ктн, доцент Василенко В. С.

Національний авіаційний університет (НАУ), Україна

Модифіковані циклічні коди

Для циклічного n-значного коду найбільш відомою, класичною процедурою кодування, тобто одержання кодової комбінації, є процедура з множенням кодової комбінації G(x) простого коду на одночлен x^k і додаванням до цього добутку залишку R(x), отриманого в результаті розподілу добутку x^kG(x) на утворюючий поліном P(x).

Наприклад, при значності коду n = 7, m = 4, k = 3 і і застосуванні утворюючого поліному Р(x) = х³ + х + 1 = 1011 кодування повідомлення
G(x) = х³ + х² + 1 = 1101 можна виконати наступним чином.

Множимо кодову комбінацію G(x) вихідного коду на одночлен x^k = х³, і одержуємо x^k·G(x) = х⁶ + х⁵ + х³. Надалі ділимо цей добуток на утворюючий поліном Р(x) = х³ + х + 1:

х⁶ + х⁵ + х³ х³ + х + 1

х⁶ + х⁴ + х³ х³ + х² + х+ 1

х⁵ + х⁴

х⁵ + х³ + х²

х⁴+ х³ + х²

х⁴+ х² + х

х³ + х

х³ + х + 1

R(x) = 1

У результаті цій операції одержимо залишок R(x) = 1.

Додаючи добуток х³G(х) до одержаного залишку, одержимо кодовий багаточлен

F(x) = x³G (х) + R (x) = х⁶ + х⁵ + х³+ 1.

У двійковому коді цьому багаточлену відповідає кодова комбінація 1101001, в якій перевірочні розряди займають три останні позиції і яку слід передавати каналом зв’язку.

В разі відсутності спотворень на приймальному боці прийнята кодова комбінація F^/(x) повністю збігається із переданою F^/(x) = F(x) = х⁶ + х⁵ + х³+ 1 і повинна ділитися на утворюючий багаточлен Р(x) без залишку:

х⁶ + х⁵ + х³ + 1 х³ + х + 1

х⁶ + х⁴ + х³ х³ + х² + х + 1

х⁵ + х⁴ + 1

х⁵ + х³ + х²

х⁴ + х³ + х² + 1

х⁴ + х² + х

х³ + х + 1

х³ + х + 1

R(x) = 0

Звернемо увагу, що при цьому процедура одержання лишку R(x) реалізується як R(x) = x^kG(x)mod P(x), коли шукана контрольна ознака обчислюється як залишок після ділення добутку x^kG(x) на P(x).

Звернемо увагу також на те, що при кодуванні (декодуванні) потрібна кількість операцій складається з: m операцій визначення чергового значення частки, m операцій множення чергового значення частки на утворюючий поліном та m операцій додавання.

Надалі більш детально розглянемо усі необхідні операції щодо обчислення лишку R(x) із використанням поліноміальної форми запису виразу для БКС, лишок якого розшукується. Ця форма запису має вигляд:

x^kG(x) = ,

де: − коефіцієнт при і –й степені основи числення (у цьому випадку, при ).

Покажемо еквівалентність виразів

(mod P(x))

та

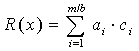(mod Р(x)).

В останньому виразі для двійкових кодів при , додавання може здійснюватися порозрядно за модулем Р = 2, а вагові коефіцієнти можуть бути обрахованими з використанням наступних міркувань.

За правилами виконання операцій по модулю перший вираз можна перетворити наступним чином:

x^kG(x) mod P(x) = {}mod P(x) =
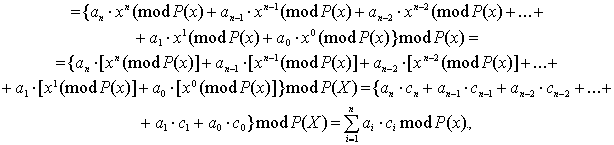де − вагові коефіцієнти при відповідних елементах представлення контрольної ознаки базового кодового слова у вигляді:

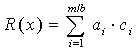(mod Р).

Отже (mod Р) = 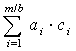(mod Р), тобто еквівалентність виразів доведена.

Звернемо увагу на те, що формування контрольної ознаки за цим виразом є модифікованим циклічним кодом.

При цьому значення вагових коефіцієнтів розрахувати не важко, оскільки вони дорівнюють лишку від ділення на утворюючий поліном коефіцієнту відповідного символу в поліноміальному представленні базового кодового слова. Нижче наведено приклади обрахування таких вагових коефіцієнтів для перших шести символів БКС при використанні утворюючого поліному (х³ + х + 1).

х⁰ : (х³ + х + 1) → R (x) = х⁰ → ; х¹ : (х³ + х + 1) → R (x) = х¹ → ;

х² : (х³ + х + 1) → R (x) = х² → ; х³ : (х³ + х + 1) → R (x) = (х + 1) → ;

х⁴: (х³ + х+ 1)→ R (x) = (х² + х )→ ; х⁵: (х³ + х + 1)→ R (x) = (х² + х + 1) →;

х⁶: (х³ + х + 1)→ R (x) = (х² +1)→ .

Результати розрахунку зводять в таблицю відповідності. Для цього прикладу таблиця має вигляд, наведений в табл. 1.

Таблиця 1

Показник ступеня х^і	Значення Е = х^і	Результат розподілу х^і/Р(x)	Двійковий еквівалент х^і/Р(x)
0	х^0 =1	х^0=1	001
1	х^1	х^1	010
2	х^2	х^2	100
3	х^3	х + 1	011
4	х^4	х^2 + х	110
5	х^5	х^2 + х + 1	111
6	х^6	х^2 +1	101

При кодуванні чи декодуванні для наочності формування контрольної ознаки інформаційні та контрольні символи зручно представляти записаними в деякий шаблон. Наприклад, для чотиризначної двійкової послідовності 1101 (m = 4) та трьохрозрядного утворюючого поліному (k = 3):

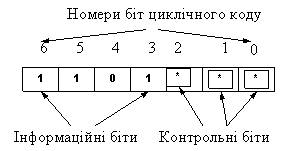
чи записаними в таблицю, наприклад таку, яка наведена нижче (табл. 2) для семизначної двійкової послідовності 1101***:

Табл. 2

Позиція біта	6	5	4	3	2	1	0
Значення біта	1	1	0	1	*	*	*

Вище невизначені спочатку значення контрольних символів помічені зірочкою (*).

Приклад кодування. Потрібно закодувати уже відоме повідомлення G(x) = х³ + х² + 1 = 1101 (m = 4) при утворюючому поліномі Р(x) = х³ + х +
+ 1 = 1011 (k = 3). Отже n = 7, і = 0, 1, …, 6.

Для формування контрольних символів здійснюється контрольне додавання шляхом виконання операції порозрядного додавання по модулю 2 кодів вагових коефіцієнтів ненульових бітів (пропускаються операції з множенням на нуль). У цьому випадку це 6, 5 і 3.

Обчислимо контрольну суму:

Таблиця 3
Номери ненульових біт	Коди ваг. коеф.
6	101
05	111
03	011
Контр. Σ	001

В результаті обчислена контрольна ознака R(x) = 001. Таким чином, приймач одержить код (табл. 4):

Таблиця 4
Позиція біта	6	5	4	3	2	1	0
Значення біта	1	1	0	1	0	0	1

Для перевірки правильності формування контрольних символів додамо знову коди ненульових бітів (табл. 5) и одержимо нуль:

Таблиця 5
Номери ненульових біт	Коди ваг. коеф.
6	101
05	111
03	011
01	001
Контр. Σ	000

Ну а тепер розглянемо два випадки помилок в одному з біт посилки, наприклад в біті 6 (0 замість 1) і в біті 2 (1 замість 0). Додамо коди ненульових біт ще раз (таблиця 6).

Пересвідчимось, що в обох випадках контрольна сума є відмінною від нуля, що свідчить про наявність спотворень та необхідність (при можливості та необхідності) їх корегування.

Таблиця 6

05	111
03	011
01	001
Σ	101

06	101
05	111
03	011
02	100
01	001
Σ	101

Звернемо увагу на те, що при кодуванні (декодуванні) модифікованим циклічним кодом потрібна кількість операцій складається лише з m операцій додавання.

Тобто, порівняно з класичною реалізацією коду кількість операцій зменшується на: m операцій визначення чергового значення частки та m операцій множення чергового значення частки на утворюючий поліном.

Таким чином, можна зробити висновок, що результати застосування запропонованої модифікації циклічного коду повністю співпадають із результатами класичного аналогу, тобто код може вирішувати задачі контролю цілісності інформаційних об’єктів, але із значно швидше.

1. Василенко В.С. Теорія інформації та кодування./ В.С. Василенко // Курс лекцій з дисципліни «Теорія інформації та кодування», К.: НАУ. – 2011. – 93 с.

2. Юдін О.К. Основи теорії електричних кіл, сигнали та процеси в електроніці./ О.К. Юдін // Курс лекцій з дисципліни «Основи теорії електричних кіл, сигнали та процеси в електроніці», К.: НАУ. – 2010. – 243 с.