Математика/ 5. Математическое моделирование

к.ф.-м.н., доцент Омаров А.М., преподаватель Есендаулетова Ж.Т.

и старший преподаватель Попова Н.В.

Карагандинский государственный университет им. Е.А. Букетова, Казахстан

Моделирование и анализ чувствительности рациональной загрузки ресурсов и эффективность технологических линий

В промышленном производстве большое значение приобретает организация выработки наиболее рациональных решений с целью повышения технического уровня производства, механизации и автоматизации производственных процессов, выявления внутренних резервов производственно-хозяйственной деятельности предприятия, лучшего использования ресурсов, сбыта продукции, решения задач технико-экономического планирования и т.д. Применение экономико-математических моделей и компьютера помогает решать такого типа задач.

С другой стороны, объем выпускаемой продукции также зависит от мощности технологического оборудования, наличия производственных мощностей, степени и порядка их использования.

Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем первой линии - 60 изделий, второй линии - 80 изделий. На радиоприемник первой модели расходуется 15 однотипных элементов электронных схем, на радиоприемник второй модели - 10 таких же элементов. Максимальный суточный запас используемых элементов равен 950 единиц. Прибыли от реализации одного радиоприемника первой и второй моделей равны 40$ и 20$ соответственно. Определите оптимальные суточные объемы производства первой и второй моделей на основе графического решения задачи.

В задаче  требуется установить, сколько радиоприемников первой и второй модели надо производить. Поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого типа радиоприемников: – суточный объем производства радиоприемников первой модели, (шт./сутки); – суточный объем производства радиоприемников второй модели, (шт./сутки). Цель задачи  – добиться максимального дохода от реализации продукции. То есть критерием эффективности служит параметр суточного дохода, который должен стремиться к максимуму. Чтобы рассчитать величину суточного дохода от продажи радиоприемников обоих моделей, необходимо знать их объемы производства, т.е. и радиоприемников в сутки, а также прибыль от их реализации  – согласно условию, соответственно 40 и 20$. Таким образом, доход от продажи суточного объема производства радиоприемников первой модели равен 40 $ в сутки, а от продажи радиоприемников второй модели – 20 $  в сутки. Поэтому запишем целевую функцию в виде суммы дохода от продажи радиоприемников первой и второй модели ($/сутки). Возможные объемы производства радиоприемников x₁ и x₂ ограничиваются следующими условиями:

- количество элементов электронных схем, израсходованное в течении суток на производство радиоприемников обоих моделей, не может превышать суточного запаса этих элементов на складе;

- суточный объем первой технологической линии (производство радиоприемников первой модели) не может превышать 60 шт. в сутки, второй (производство радиоприемников второй модели) – 80 шт.;

- объемы производства радиоприемников не могут быть отрицательными.

Таким образом, все ограничения задачи делятся на 3 группы, обусловленные 1) расходом элементов электронных схем; 2) суточным объемом технологических линий; 3) неотрицательностью объемов производства. На основании данных ограничений получим математическую модель:

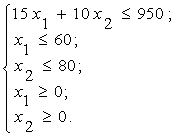
Используя графический метод, получим (см. рисунок 1).

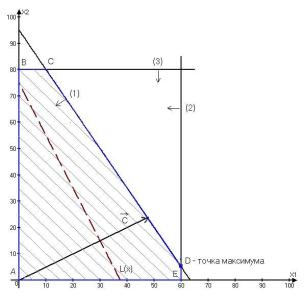
Рис. 1. Графическое решение задачи о производстве радиоприемников.

Здесь точка  – это точка максимума целевой функций. Максимальное значение целевой функции равно ($/сутки). Таким образом, наилучшим режимом работы предприятия является ежесуточное производство радиоприемников первой модели в количестве 60 штук и радиоприемников второй модели в количестве 5 штук. Доход от продажи составит 2500$ в сутки [1].

Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение поставленной задачи.

Проанализируем чувствительность оптимального решения задачи о производстве радиоприемников. Область допустимых решений задачи (см. рисунок 2) – многоугольник ABCDE. В оптимальной точке D пересекаются прямые (1) и (2). Поэтому ограничения (2) и (3) являются связывающими, а соответствующие им ресурсы (суточный объем элементов электронных схем и производительность первой технологической линии) – дефицитными.

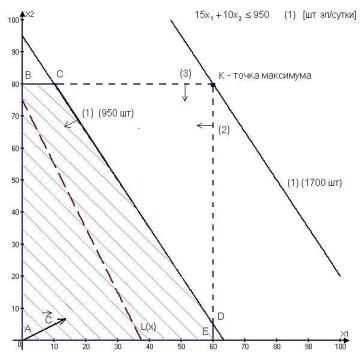
Рис. 2. Анализ увеличения суточного запаса элементов электронных схем.

Рассмотрим экономический смысл этих понятий. Точка максимума целевой функции D соответствует суточному производству 60 шт. радиоприемников первой модели и 5 шт. радиоприемников второй модели. В производстве радиоприемников используются однотипные элементы электронных схем. Суточный запас на складе этих элементов – это правая часть связывающего ограничения (2) (950 шт./сутки). Согласно этому ограничению, на производство в точке D расходуется (шт. элементов/сутки) (2).

Предложение 1. Чтобы графически определить максимальное увеличение запаса дефицитного ресурса, вызывающее улучшение оптимального решения, необходимо передвигать соответствующую прямую в направлении улучшения целевой функции до тех пор, пока это ограничение не станет избыточным. При прохождении прямой (2) через точку К (см. рисунок 2) многоугольник ABKE становится областью допустимых решений, а ограничение (2) – избыточным. Действительно, если удалить прямую (2), проходящую через точку К, то область допустимых решений ABKE не изменится. Точка К становится оптимальной, а ограничения (2) и (3) в этой точке становятся связывающими.

Предложение 2. Чтобы численно определить максимальную величину запаса дефицитного ресурса, вызывающую улучшение оптимального решения, необходимо: 1) определить координаты точки , в которой соответствующее ограничение становится избыточным; 2) подставить координаты , в левую часть соответствующего ограничения.

Координаты точки находятся путем решения системы уравнений прямых (2) и (3), т.е. в сутки предприятие будет производить 60 шт. радиоприемников первой модели и 80 шт. радиоприемников второй модели. Подставим и в левую часть ограничения (1) и получим максимально допустимый запас элементов электронных схем (шт. эл./сутки).

Дальнейшее увеличение запаса элементов электронных схем нецелесообразно, потому что это не изменит область допустимых решений и не приведет к другому оптимальному решению (см. рисунок 2). Доход от продажи радиоприемников в объеме, соответствующем точке К, можно рассчитать, подставив ее координаты в выражение целевой функции ($/сутки).

Рассмотрим теперь вопрос о целесообразности увеличения производительности первой технологической линии. Согласно педложению 1, соответствующее ограничение (2) становится избыточным в точке J, в которой пересекаются прямая (1) и ось переменной х₁ (см. рисунок 3). Многоугольник ABCJ становится областью допустимых решений, а точка (или (63; 0)-целочисленное решение) – оптимальным решением.

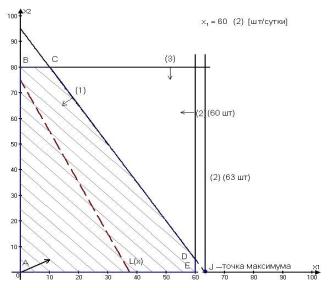
Рис. 3. Анализ увеличения производительности первой технологической линии.

В точке J выгодно производить только радиоприемники первой модели (63 шт. в сутки). Доход от продажи при этом составит

($/сутки)

Чтобы обеспечить такой режим работы, согласно предложению 2, производительность первой технологической линии надо увеличить до величины (шт./сутки).

Ограничение (3) является несвязывающим, так как не проходит через оптимальную точку D (см. рисунок 4). Соответствующий ему ресурс (производительность второй технологической линии) является недефицитным. С экономической точки зрения это означает, что в данный момент уровень производительности второй технологической линии непосредственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке D.

Например, увеличение (уменьшение) суточного объема второй технологической линии будет соответствовать перемещению прямой ограничения (3) вверх (вниз). Перемещение прямой (3) вверх никак не может изменить точку D максимума целевой функции. Перемещение же прямой (3) вниз не влияет на существующее оптимальное решение только до пересечения с точкой D.

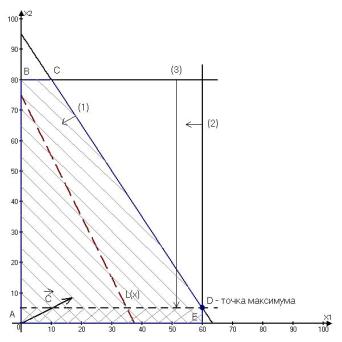
Рис. 4. Анализ уменьшения производительности второй технологической линии.

Из рисунка 4 видно, что дальнейшее перемещение (3) приведет к тому, что точка D будет за пределами новой области допустимых решений, выделенной более темным цветом. Кроме того, любое оптимальное решение для этой новой области допустимых решений будет хуже точки D.

Предложение 3. Чтобы определить максимальное уменьшение запаса недефицитного ресурса, не меняющее оптимальное решение, необходимо передвигать соответствующую прямую до пересечения с оптимальной точкой. Чтобы численно определить минимальную величину запаса недефицитного ресурса, не меняющую оптимальное решение, необходимо подставить координаты оптимальной точки в левую часть соответствующего ограничения.

Чтобы выяснить, до каких пределов уменьшение производительности второй технологической линии не повлияет на производство в точке D, используем предложение 3. Подставляем в левую часть ограничения (3) координаты точки D, получаем (шт./сутки).

Результаты решения задачи анализа оптимального решения на чувствительность представлены в таблице 1.

Таблица 1 Результаты решения задачи анализа оптимального решения на чувствительность

№	Тип ресурса	Max изменение ресурса, шт./сутки	Max изменение дохода, $/сутки	Ценность дополнительной единицы ресурса $/шт.
(1)	Дефицитный
(2)	Дефицитный
(3)	Недефицитный

Отсюда следует три вывода:

1) Увелечение запаса сырья в данном случае элементов электронных схем ограничивается предельным значением.

2) Производительность первой технологической линиий для данной задачи зависить только от выпуска первого вида продукции.

3) Производительность второй технологической линий не влияет на производство до определенных пределов.

Литература:

1. Букан Дж., Кенинсберг Э. Научное управление запасами. - М.: Наука, 1997.-296с.