МАТЕМАТИКА

1.Дифференциальные и интегральные уравнения

Преподаватель Захарченко Н.В., Бектурсунов Д.Н., Севастеев Е.А., Горохов Ю. С.

Одесская национальная академия связи им. А.С. Попова

 

Определение координат таймерных сигналов, удовлетворящих условию качества

 

 

На основании решения диафантовых уравнений предложен метод определения координат векторов избыточных таймерных синалов, удовлетворяющих условию качества  

 

Таймерные сигналы[1,2] представляют собой такие конструкции, в которых кодовое расстояние определяется нецелым числом найквистовых элементов. Информация заложена в длительностях отдельных временных отрезков сигнала  на интервале Тск и их взаимном положении. Элементом синтеза кодовой конструкции является временной отрезок <t0, однако в процессе передачи по каналу с базой , после очередного значущего момента модуляции(ЗММ) передается s раз очередной сигнал аі из алфавита канала.

Так как базовый элемент <t0  по каналу связи без межсимвольных искажений передавать невозможно, а следовательно существующая алгебраическая теория кодирования для таймерных сигналов неприемлема. С целью уменьшения межсимвольных искажений длительность отрезков между соседними ЗММ одного и тогоже кодового слова (КС) не меньше найквистового интервала (), но и не кратна ему . Временной отрезок  представляет часть единичного элемента  () и определяется минимальной вероятностью ошибки приёма одного значащего момента воспроизведения (ЗМВ) в „хорошем” состоянии канала и соответствуют минимальному расстоянию между простыми ТСК. Таймерные сигнальные конструкции используются в каналах модели Гильберта, которые отличаются тем, что имеют два рабочих состояния [3]. Для различия “хорошого” и “плохого” состояний канала используется уравнение качества , при помощи которого вводятся дополнительные ограничения для оценки правильного приема сигнала.

Существует два вида таймерных конструкций: простые, описанные выше, расстояние между ближайшими кодовыми словами составляет  и избыточные, у которых расстояние между кодовыми словами определяется параметрами избыточности исходя из уравнения качества. Избыточные кодовые слова требуют большее число реализаций для одного и того же множества разрешенного к передаче по каналу связи. Например, для построения простого таймерного кода, который обеспечивает передачу одного байта(256 различных кодовых слов) необходимо  [1] . Легко посчитать, что ближайшее число реализаций можно получить при .

Для получения избыточных кодовых слов, удовлетворяющих, например, неравенству   необходимо обеспечить 256*19=4864 простых кодовых слова, из которых только 256 разрешены к передаче, то есть удовлетворяют условию качества.  Такое число кодовых слов можно реализовать на интервале . Из этого следует, что временные затраты на передачу одной избыточной конструкции возрастут в 1,61 раза, что однако меньше времени передачи одного байта  при помощи РЦК (), и, как показывают исследования, обеспечивают вероятность ошибки в канале связи 10-7.[4]

В данной работе предложен метод определения координат векторов избыточных таймерных сигналов, удовлетворяющих условию качества и позволяющий оценить правильность приема вектора кодового слова на приемной стороне.

Рассмотрим систему таймерных сигналов, удовлетворяющих условиям

(1)
 

где  отрезки состоящие из  и соответствуют расстояниям между ЗММ.

Определим количество кодовых слов, удовлетворяющих условию (1) при двух и трех ЗММ.

Для двух ЗММ проверочное условие для отбора кодовых слов имеет вид

                                                        (2)

В [5] доказано, что для   , ,

Равенство (2) можно записать в виде:

                                                 (3)

где x0, x1, x2 – целые числа. При этом в силу выбора A1 и A2

 

Из формулы (2) следует, что векторы

,

.

 

удовлетворяют условию (3). Любой вектор , такой, что  можно представить в виде , то есть

 

 

(4)

 

 

 

Из значений переменной xi  (4) следует, что координаты  будут целыми числами тогда и только тогда, когда – целые. Из ограничений описанных выше видно, что для того чтобы вектор  был кодовым словом, x1 и  x2 должны изменяться в таких пределах:

 

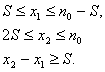                                                                                          (5)

где  n0 – максимальное число элементов между ЗММ.

Так как x1 и  x2 можно определить по формуле (4), рассмотрим пределы в которых могут изменяться  и , чтобы выполнялись условия (5). Количество кодовых слов зависит от количества различных пар  и . Найдем пределы изменения x0

Пусть

 

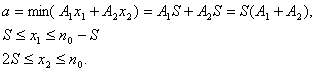
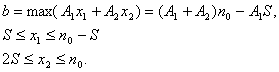
В силу (3) легко заметить, что

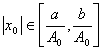                                                                     (6)

Теперь на основании формул (4)-(6) запишем

 

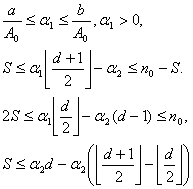                                                          (7)

 

Обозначим

Откуда для  получаем неравенства

                                         (8)

 

Теперь, чтобы найти кодовые слова поступим следующим образом: рассмотрим все целые числа, принадлежащее 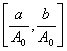. Это те значения, которые может принимать . Для каждого фиксированного значения 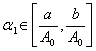 решаем систему неравенств (8) для определения значений , которые могут быть использованы совместно с данными . Найдем все целые числа отрезка , где

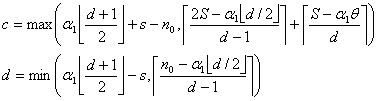
Для каждого целого  находим количество целых чисел, принадлежащих отрезку [c, d]. Обозначим это количество . Число кодовых слов равно

При вычислении числа кодовых слов , рассмотрена совокупность всех пар  и , определяемых неравенствами (7) и (8). Рассмотрим матрицы:

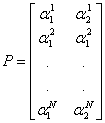 и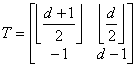

 

Составив произведение матриц P·T=S, где

 

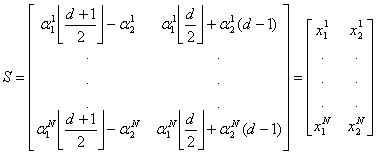                                               (9)

 

Строки матрицы S и будут координатами кодовых слов.

Количество кодовых слов при трех ЗММ определяется аналогично.

Опустим расчеты, которые вытекают из [5] и аналогичны описанным выше, приведем лишь результаты вычислений:

 

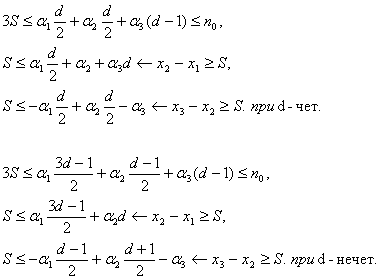                                   (10)

Для каждого значения  найдем отрезок , все целые числа которого есть возможные значения . Аналогично значения  , — это все целые числа  на отрезке . Множество кодовых слов, будет получено путем полного перебора , , , удовлетворяющих  условию (10).

Рассмотрим проверочное условие для трех переходов с пересекающимися зонами:

 

                                                            (11)

Введем  вспомогательное значение

                                                        (12)

Получим из (11) неравенства для

                                                  (13)

Уравнение качества представим в виде  Принимая во внимание (11), делаем вывод, что PA0 принимает целые значения на отрезке .

 

При помощи данного метода можно получить набор кодовых слов для реализации таймерного сигнала с любым количеством ЗММ, которые удовлетворяют условию качества, а значит могут быть верно декодированы на приемной стороне.

 

Литература

1.             Захарченко М.В. Синтез багатопозиційних часових кодів – К.:Техніка, 1999. – 284 с.

2.             Методы повышения эффективности использования каналов связи /Захарченко В.Н., Гайда В.П., Улеев А.П., Липчанский А.И. – К.:Техника, 1998. – 248 с.

3.              Захарченко Н.В., Йона Л.Г., Калюжный В.А. Расчет эффективности совместного использования РЦК и МВС.: Учебное пособие / под.. ред. Захарченко Н.В. – Одесса: УГАС им. А.С. Попова, 1995. – 72 с.

4.             Захарченко М. В., Ефективність корегуючих ТСК в односторонніх системах передачі./ М. В. Захарченко, М.М. Гаджієв, С. В. Хомич, М.П. Кучеренко // Східно-європейський журнал передових технологій. – 2012. – Вип. 1/9. – с. 33-36.

5.       Захарченко М. В., О все вектора таймерного кода, удовлетворяющего условию качества ./ Захарченко Н.В., Бектурсунов Д.Н., Лысенко С.И., Севастеев Е.А.//  Вимірювальна та обчислювальна техніка в технологічних процесах. -2013. – Вип. № 1(42). – с. 226-232