Математика/5. Математическое моделирование

К. т. н. Цветков А.Б., д.т.н., доцент Павлова Л.Д.

Сибирский государственный индустриальный университет, Россия

РАЗРАБОТКА Дискретной модели геомеханического состояния углепородного массива для пакетов символьной математики

 

На сегодня подавляющее количество программ разрабатывается на языках программирования С, Pascal, Fortran и основанных на них средах разработки, которые позволяют создавать переносимые приложения в виде исполняемых модулей. В конце прошлого века среди специалистов для решения научно-технических задач стали популярны системы символьной математики такие, как MathCAD, MATLAB, Maple, Mathematica. Но вычисления в этих системах проводились медленно по сравнению с приложениями, написанными на языках программирования. В связи с развитием этих систем проводилась их оптимизация, и увеличилась скорость вычислений.  Вследствие чего, стали появляться  прикладные пакеты программ, разработанные в системах символьной математики, предназначенные для решения технических задач. Например, пакет FemLAB основан на системе символьной математики Maple, Simulink  - MATLAB  и др. Ускорение вычислений в этих пакетах позволило решать системы   линейных уравнений высокого порядка за приемлемое время, что позволило рассматривать системы символьной математики как полноценные пакеты для математического моделирования. Приложения, разработанные в этих системах, способны конкурировать по быстродействию с программами, разработанными на языках программирования.

В основе численного решения большинства краевых задач нашедших применение на практике находится метод конечных элементов в виду его адаптированности для средств вычислительной техники.  Исходя из специфики языков программирования дискретные модели, полученные на основе метода конечных элементов, реализованы в матричном виде. Но для систем символьной математики  матричная форма представления модели не обязательна. Поэтому, актуальным является вопрос разработки дискретных моделей сразу в форме уравнений, так как матричная форма записи является ее частным случаем.

В статье приведена дискретная модель геомеханического состояния массива, сформированная в виде системы алгебраических уравнений.

Краевая задача теории упругости, применяемая при решении задач геомеханики, на плоскости XOY имеет вид [1]:

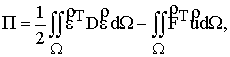                                                                          (1)

где Fx, Fy – массовые силы,  - вектор деформаций.

Краевая задача на плоскости решена методом конечных элементов [1]. В качестве конечного элемента выбран лагранжев четырехугольник  с билинейной аппроксимацией вектора перемещений – (рисунок 1).

 

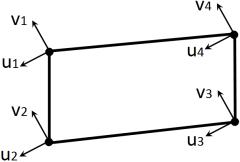
Рисунок 1 - Четырехугольный конечный элемент

 

Как было показано в работе [2] решение краевой задачи теории упругости для горизонтально-слоистой прямоугольной области имеет порядок не ниже второго. Этим обоснован выбор билинейной аппроксимации.

Четырехузловые конечные элементы удобны для геометрического описания  пластовых геоструктур. С помощью таких элементов помимо синтеза геометрической модели исследуемого участка удобно формировать выборки по вертикальным сечениям для построения графиков перемещений, деформаций и напряжений. На рисунке 2  приведена дискретизация четырехугольными конечными элементами сечения геомассива, включающего три пласта, мощность одного из которых варьируется.

 

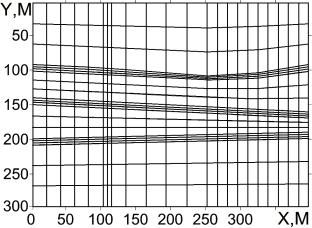
Рисунок 2 – Дискретизация расчетной области

 

Из рисунка 2 видно, что с помощью выбранных конечных элементов можно задавать нерегулярные сетки, которые позволяют задавать особенности  изучаемого участка геомассива, например, такие  как наклонные пласты, синклинали,  антиклинали и локальное сгущение сетки.

Пусть заданы координаты , , ,   вершин конечного элемента. Аппроксимация горизонтальной и вертикальной компоненты вектора перемещений на четырехугольном конечном элементе задана виде:

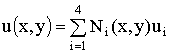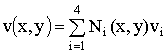                                  , ,                (2)

где  - вектор перемещений, ,  - горизонтальная и вертикальная компоненты, , - искомые узловые значения, i=1,2,…,4,  - функции формы.  

Базисные функции  были получены с помощью интерполяционного подхода. Базисная функция  должна иметь значение 1 в i-м узле и нулевые значения во всех трех остальных.  Например,  функция формы для узла №1 определяется равенством:

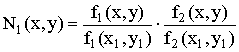                                           ,                            (3)

где  и  уравнения прямых, проходящих через точки ,  и , :

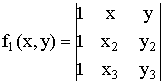                                  ,                  (4)

Функция  обращается в ноль в точках ,     и не равна нулю в точке . Аналогично функция  обращается в ноль в точках ,   и не равна нулю в точке . Следовательно, функция  равна единице в первом узле и нулю во всех остальных узлах - 2, 3, 4. Аналогично получены функции формы для остальных узлов , , .

Дискретная модель, адаптированная для систем символьной математики из  (1) строилась объединением по узлам. Для этого квадратичная форма:

                                                                        ,                                                    (5)

с использованием матрицы упругости, вектора деформаций:

,

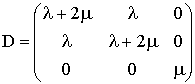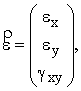
соотношений Коши:

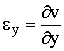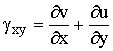                                        , ,                             (6)

преобразована в функцию от перемещений и после подстановки ее в функционал (1)  он принял вид:

                                                 П=П1+П2+П3+П4,                                           (8)

где μ, λ – параметры Ламе,

                                ;

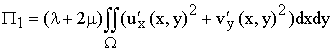                                        ;                             (9)

                                      ;

                                          .

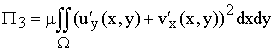Расчетная область  разбита на конечные элементы:

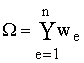                                                          ,                                             (10)

где  - число конечных элементов.

Аппроксимация горизонтальной и вертикальной компоненты вектора перемещений на каждом конечном элементе задана виде:

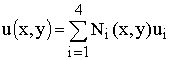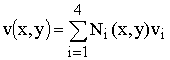                            , .                    (11)

После дискретизации расчетной области функционал (9)  примет вид:

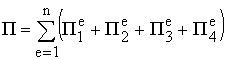                                           ,                               (12)

где

                             ;

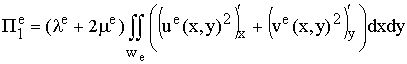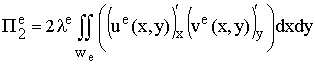                                    ;                    (13)

                                    ;

                                           ,

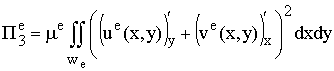n – число конечных элементов.

Функционал (12) является квадратичной формой узловых перемещений  ,  , где k=1..4 номер узла конечного элемента .

Величины  и   находятся из условий минимума функционала  (12):  

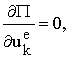
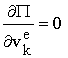                                                     ,                                       (14)

где  - число конечных элементов, k=1..4 – номер узла конечного элемента. Частные производные это  линейные функции от узлов.

Для каждого узла сетки составляется система (14) и ансамблируется в глобальную систему линейных алгебраических уравнений.  Учет граничных условий производится посредством вычеркивания из системы уравнений, номера которых равны номерам запрещенных перемещений.

Таким образом, получена дискретная математическая модель для систем символьной математики в виде  системы линейных алгебраических уравнений, адаптированная для систем символьной математики. На основе разработанной дискретной модели, представленной СЛАУ можно в частном случае получить коэффициенты глобальной матрицы жесткости, посредством взятия производных по узловым перемещениям.

 

Литература:

1.     Зенкевич О. Метод конечных элементов в технике. – М.: Мир, 1975 – 271 с.

2.     Синтез краевой задачи теории упругости и статического давления для математического моделирования напряженно-деформированного состояния в угольном пласте и вмещающих породах при действии гравитации. / А.Б. Цветков, П.В. Васильев, О.А. Петрова //Горный информационно-аналитический бюллетень. - М.: Горная книга, 2012. – №12. – С. 3-9.