Математика/ Математическое моделирование

К. ф.-м.н. Камалова Г.А.

Западно-Казахстанский аграрно-технический университет им. Жангир хана, Казахстан

Численное моделирование взаимодействия потоков твердых частиц и газа

Математическое моделирование течений гетерогенных сред связано с межфазным взаимодействием трения и теплообмена между газом и дисперсными частицами [1,2]. Соответственно изучение движения гетерогенных смесей с учетом исходной структуры смеси и физических свойств фаз связано с привлечением новых параметров (обмен импульса, тепла) и решением уравнений более сложных, чем те, с которыми приходится иметь в механике однофазных, т.е. гомогенных сред. При этом детальное описание межфазных взаимодействий в гетерогенных средах порою чрезвычайно сложно, и для получения результатов и их понимания здесь особенно необходимы рациональные схематизации, приводящие к обозримым и решаемым уравнениям. Цель данной работы – разработка численной модели плоского течения газовзвеси (газ–твердые частицы).

Постановка задачи. Рассматривается плоское течение аэросмеси турбулентной струи (аэросмесь, состоящая из твердых частиц и воздуха), истекающей из сопла в прямоугольный канал с частично открытой правой границей.

Основные допущения, используемые в математической формулировке задачи:

- несущая фаза – воздух, дисперсная фаза состоит из твердых частиц;

- твердые частицы имеют сферическую форму и состоят из твердого скелета, в порах которого содержится газ (далее будем называть летучими);

- в результате нагрева частиц за счет теплообмена происходит выделение летучих газов;

- частицы предполагаются сухими, т.е. влажность ;

- лучистым теплообменом между частицами и поверхностью пренебрегается.

При этих допущениях исходной для смеси газов служит система осредненных по Рейнольдсу уравнений Навье-Стокса, записанных в безразмерной форме в общепринятых обозначениях.

Исходными для частиц являются система лагранжевых уравнений изменения масс, моментов и энергии частиц. Дополнительные члены, появляющиеся за счет межфазного обмена импульса, массы и энергии и силами сопротивления. Выделение летучих газов вследствие конвективного теплообмена определяется следующим образом.

Начальные и граничные условия. Рассматриваемая задача решается со следующими постановками начальных и граничных условий. В начальный момент газ находится в состоянии покоя, задаются плотности компонентов, распределение температуры постоянно, кинетическая энергия турбулентности и масштаб турбулентности также постоянны.

На входе задаются: внутри сопла - аэросмесь (частицы + первичный воздух), во внешней части сопла - вторичный воздух. На стенках: для поля скорости задается турбулентный закон стенки, тангенциальный компонент скоростей, которого определяется приближенным соотношением, полученным с помощью логарифмического профиля и степенного закона.

Для кинетической энергии турбулентности, концентраций компонентов газа выполняется условие отсутствия потока через стенку. Связь между кинетической энергией турбулентности и скоростью ее диссипации задается. Для твердых частиц задается условия прилипания.

На выходе: для газовой фазы задаются мягкие граничные условия. Частицы вблизи открытой границы покидают рассматриваемую область.

Выход газов из твердых частиц. Процесс термического разложения частиц – кинетический. Во многих экспериментальных работах механизм выхода летучих изучался на крупных одиночных частицах при неограниченном избытке воздуха и при высоких температурах. Численно моделируется выход летучих газов из твердых частиц за счет конвективного теплообмена.

В работе приняты в качестве частиц угольные частицы, состоящее из сырого угля, кокса и золы, и вследствие конвективного теплообмена происходит термическое разложение органической массы угольного топлива с выделением летучих газов, таких как, метан , окись углерода и ацетилен . В соответствии с изложенными допущениями задается плотность сферической частицы. При этом предполагается, что радиус частицы не меняется.

Метод решения. Детальное описание численного метода решения системы уравнений Навье-Стокса, а также тестирование построенного алгоритма изложено в работах [3,4]. Дискретизация уравнений осуществляется методом контрольного объема со вторым порядком точности по пространственным переменным. Построенные конечно-разностные уравнения решаются трехэтапной схемой расщепления по физическим процессам: влияние дисперсной среды на газовую фазу вычисляется явным образом; промежуточные значения скоростей, температуры и давления с учетом диффузии вычисляются методом предиктора-корректора и сопряженных разностей; конвективный перенос рассматриваемых величин определяется с использованием схемы донорной ячейки.

Результаты расчетов и их анализ. Расчет производился на сетке по пространственным координатам размером 60х100 с шагами , . Диаметр внутреннего сопла , а внешнего . Рассматривается течение в канале, в котором производится вдув аэросмеси через отверстие размером с температурой . При этом расход частиц . Начальная температура в канале составляет . Движение частицы в канале является свободным, т.е. они попадают в рассматриваемую область случайным образом.

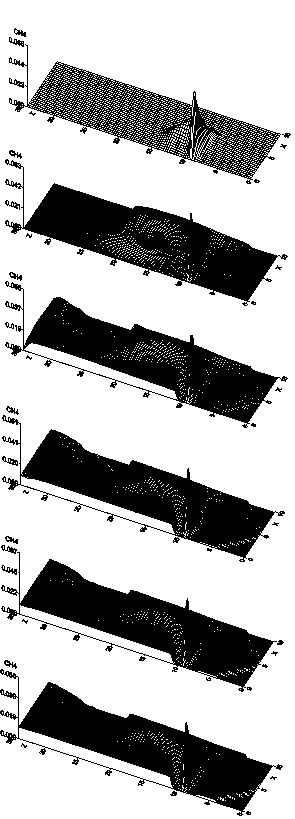
Ниже приводится анализ результатов исследования процесса термического разложения частиц, т.е. выделения летучих компонентов. Как было указано выше, при теплообмене между частицей и газом происходит термическое разложение частиц по кинетической схеме, в результате которого осуществляется выход летучих компонентов, таких, как окиси углерода и метана . На рисунке 1 показана динамика образования летучих компонентов окиси углерода и метана . Из картин наблюдается, что к моменту времени в местах максимальной концентрации твердых частиц, т.е. в центре области, образуются летучие газы. Максимум окиси углерода составляет 0.16 (рисунок 1А), а метана 0.066 (рисунок 1Б), что и является естественным, так как концентрация в угольной частице была существенно. Из рисунков следует, что с течением времени летучие газы сносятся потоком вверх.

ЛИТЕРАТУРА

1 Стернин Л.Е., Маслов Б.Н., Шрайбер А.А., Подвысоцкий А.М. Двухфазные моно- и полидисперсные течения газа с частицами. – М.: Машиностроние, 1980. – 172 с.

2 Вараксин А.Ю. Турбулентные течения газа с твердыми частицами. – М.: Физматлит, 2003. – 192 с.

3 Камалова Г.А., Найманова А.Ж. Математическое моделирование газодинамических процессов двухфазной среды в устройствах различной конфигурации // Математический журнал. – 2005. – №1. – С. 52-66.

4 Kamalova G.A., Messerle V.E., Naimanova A.Zh., Ustimenko A.B. Modelling of Turbulent Reacting Flows in Furnace Devices // Thermophysics and Aeromechanics. – 2008. – Vol. 15, No 1. – P. 139 – 151.

А Б

е)

д)

г)

в)

б)

а)

а) , б) , в) , г) , д) , е) .

Рисунок 1 – Динамика образования летучего компонента (А) и (Б)