Литвин О. М., Бондаренко А. О.

м. Бердянськ, Бердянський державний педагогічний університет

academ_mail@ukr.net, alena_kurasova@mail.ru

ВІДНОВЛЕННЯ ВНУТРІШНЬОЇ СТРУКТУРИ ТІЛА ЗА ДОПОМОГОЮ МІШАНОЇ АПРОКСИМАЦІЇ

Постановка проблеми. Слово томографія об’єднує нові, перспективні напрями отримання та обробки інформації про досліджуваний об’єкт методами рентгенодіагностики та іншими методами, які дозволяють отримувати зображення перетинів об’єкту. В багатьох працях з томографією пов’язується новий метод діагностики – метод комп’ютерної томографії (КТ) – чисельного відновлення функцій 2-х і більше змінних за відомими їх лінійними інтегралами (вздовж послідовності прямих), або площинними інтегралами (інтегралами по послідовності площин).

Помітне зростання досліджень в області томографії пов’язані з її можливістю "заглянути" всередину об’єкта не руйнуючи його. Така можливість знайшла широке застосування в медицині при діагностиці різних захворювань. Широко відомою томографія стала дякуючи появі та удосконаленню медичних томографів (в першу чергу – рентгенівських – РКТ) та тому, що у багатьох випадках результати, отримані з допомогою КТ, не можуть бути отримані ніякими іншими методами.

У розвиток малоракурсної КТ (МРКТ) значний вклад внесли Shepp L. A., Logan B. F., Пікалов В. В., Казанцев І. Г., Філонін О. В., Губарені Н. М., Сергієнко І. В., Литвин О.М. та інші. В останній чверті 20-го століття і на початку 21-го століття інтенсивно розвивається новий напрям в теорії наближення.

Зауважимо, що оператор мішаної апроксимації відновлює функції (можливо, наближено) за відомими їх слідами на даній системі ліній або поверхонь. Тобто, він надає можливість будувати наближуючі оператори, що використовують інтеграли від відновлюваної функції по вказаних лініях чи поверхнях. Звідси витікає, що мішана апроксимація є математичним апаратом, природно пов'язаним із задачею відновлення характеристик об'єктів за відомими їх проекціями. Тобто, актуальною є задача дослідження можливостей мішаної апроксимації функцій для розв’язання задачі МРКТ, зокрема ультрамалоракурсної КТ.

Аналіз публікацій. Значний внесок у розвиток комп’ютерної томографії внесли Р.М. Луїтт, А.Н. Тихонов, В.Я. Арсенин, М.В. Синьков, Н.М. Губарени, О.М. Литвин, Ю.І. Першина та інші.

Існує ряд задач (в основному, це - задачі з неповним набором проекцій), які не можуть бути ефективно розв’язані методами класичної комп’ютерної томографії. Дослідженням таких задач займається малоракурсна КТ (МРКТ). У її розвиток значний вклад внесли В.В. Пикалов, О.М. Литвин, І.В. Межуєв та інші.

Оскільки, оператори інтерлінації, інтерфлетації та мішаної апроксимації відновлюють функції (можливо, наближено) за відомими їх слідами на даній системі ліній або поверхонь. То звідси витікає, що інтерлінація, інтерфлетація та мішана апроксимація є математичним апаратом, природно пов'язаним із задачею відновлення характеристик об'єктів за відомими їх проекціями. Тобто, актуальною є задача дослідження можливостей інтерлінації та мішаної апроксимації функцій для розв’язання задачі МРКТ, зокрема ультрамалоракурсної КТ .

Мета статті: є систематизація нових методів розв’язання плоскої і просторової задач комп’ютерної томографії з використанням інтерлінації та мішаної апроксимації функцій.

Виклад основного матеріалу. Завдяки науковим відкриттям вчених-математиків (О.М. Литвин, Ю.І. Першина та ін.) з’явилася змога значно підвищити ефективність розв’язання задач комп’ютерної томографії на основі двох рентгенівських знімків у двох взаємно-перпендикулярних ракурсах. Для побудови математичної моделі внутрішньої структури тривимірного тіла будемо використовувати мішану апроксимацію сумами Фур’є функцій трьох змінних за змінними побудовану за допомогою сум Фур’є функцій порядків за змінними відповідно

Ці оператори мають вигляд

де

.

Для того, щоб ці математичні результати використати при математичному моделюванні внутрішньої структури тривимірного тіла за допомогою двох рентгенівських знімків у напрямах осей та , відповідно, зауважимо, що доданок

у формулі може розглядатися, як функція змінних , що описує зображення на рентгенівському знімку, яке отримується в результаті просвічування об’єкта (вважаємо, що об’єкт дослідження повністю розміщений у кубі ) рентгенівськими променями вздовж осі при умові, що рентгенівський промінь проходить через точку площини .

Аналогічно визначається для доданку у формулі .

Зауваження. Замість проекції отриманої інтегруванням вздовж можна використати проекцію сумісно з проекцією . Аналогічне зауваження виконується і для того випадку, коли замість проекції c отриманої інтегруванням вздовж осі використати проекцію сумісно з проекцією .

Приклад. Функція 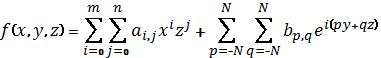точно відновлюється оператором .

Дійсно,

Висновки. За допомогою мішаної апроксимації та заданих рентгенівських знімків можливо відтворити внутрішню структуру тіла не порушуючи його цілісності. В теорії наближення функції однієї та багатьох змінних на даний час отримані результати, що дозволяють будувати оператори наближення функцій із потрібною точністю і такі, що вимагають для цього мінімального числа експериментальних даних. З’являється можливість запропонувати математичну модель придатну для комп’ютерної обробки, яка може бути використана для роботи комп’ютерного томографа. Ця модель має бути ергономічною та універсальною.

Література

1. Губарени Н.М. Вычислительные методы и алгоритмы малоракурсной компьютерной томографии / Н. М. Губарени. – Киев : Наукова думка, 1997. – 326 с.

2. Литвин О.М. Метод наближеного розв’язання однієї плоскої задачі комп’ютерної томографії / О. М. Литвин, О. О. Литвин. – 11 Міжнародна наукова конф. Імені академіка М. Кравчука. 18-20 травня 2006 року. Матеріали конф., Київ, 2006. – С. 491.

3. Литвин О. М. Інтерлінація функцій та деякі її застосування / О. М. Литвин. – Харків : Основа, 2002. – 545 с.

4. Першина Ю.І. Математичне моделювання в комп’ютерній томографії з використанням інтерфлетації функцій : автореф. к.ф.-м.н. : спец. 01.05.02 «Матем. моделювання і обчислювальні методи» / Ю. І. Першина. – Харків, 2007.

5. Сергієнко І.В., Литвин О.О. Математичне моделювання внутрішньої структури 3D тіла на основі двох рентгенівських знімків у двох взаємно-перпендикулярних ракурсах. Доповіді НАН України, №6, 2008. – С. 40–45.

6. Терещенко С.А. Методы вычислительной томографи / С. А. Терещенко. – М. : Физматлит, 2004. – 320 с.

7. Трофимов О.Е. К задаче восстановления функции трех переменных по ее интегралам вдоль прямых, пересекающих заданную кривую / О. Е. Трофимов // Автометрия. – 1991. – № 5. – с. 57–64.

8. Хелгасон С. Преобразование Радона / С. Хелгасон. – М. : Мир, 1983. – 152 с.