УДК 378

НЕУЛУЧШАЕМАЯ ОЦЕНКА СКОРОСТИ СХОДИМОСТИ МЕТОДА ФИКТИВНЫХ ОБЛАСТЕЙ ДЛЯ НЕЛИНЕЙНОЙ КРАЕВОЙ ЗАДАЧИ ЭЛЛИПТИЧЕСКОГО ТИПА

Тукенова Ляйля Муратбековна

к.ф.-м.н., доцент кафедры «Прикладная информатика»

Казахский экономический университет имениТ.Рыскулова, Алматы

Калдарова М, Козыбагарова Н., Шинасилов Ш.

магистранты 2 курса, спец. «ВТиПО», КазЭУ имениТ.Рыскулова, Алматы

Е-mail: tuken_lei06@mail.ru

NON-IMPROVED CONVERGENCE RATE ESTIMATE FICTITIOUS DOMAIN METHOD FOR NON- LINEAR BOUNDARY VALUE PROBLEMS OF ELLIPTIC TYPE

Tukenova Lyailya Muratbekovna

Associate Professor of "Applied informatics" Kazakh Economic University

named after T. Ryskulov, Almaty, Kazakhstan.

Kaldarova M., Kozybagarova N., Sh. Shinasilov.

2nd course of undergraduates, spec. "VT&PO" Kaz EU named after T.Ryskulov, Almaty

АННОТАЦИЯ

В работе рассматриваются варианты метода фиктивных областей для нелинейных эллиптических уравнений. Выведена неулучшаемая оценка скорости сходимости решения метода фиктивных областей.

ABSTRACT

The versions of fictitious domains method for nonlinear elliptic equations. The non-improved convergence speed estimation has been obtained.

Ключевые слова: метод фиктивных областей, граница, неулучшаемая оценка.

Keys words: fictitious Domains method, non-improved convergence.

Постановка задачи. Рассмотрим в области Ω с границей S краевую задачу для нелинейных эллиптических уравнений [1]

(1)

(2)

Задачу (1), (2) решаем методом фиктивных областей нового варианта в области D [2], [3]

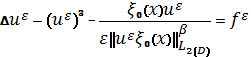, (3)

(4)

где

(5)

S₁ - граница области D.

Изучении поведение решения задачи (3), (4). Следует отметит, что, если допустить то очевидно, и

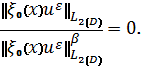(6)

Cледовательно,

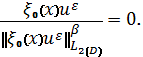(7)

Определение 1. Обобщенным решением задачи (3),(4)называется функция и^�� удовлетворяющая интегральному тождеству

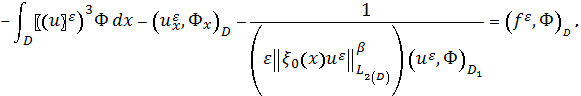(8)

для каждого Ф

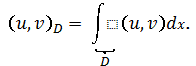
Тогда справедлива следующая теорема.

Теорема 1. Пусть тогда существует хотя бы одно обобщенное решение задачи (3),(4) и для него имеет место оценка

(9)

где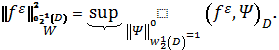

Оценка легко следует из интегрального тождества (8), если положить в нем Ф= и применить на правую часть неравенства Шварца и Коши

Теорему 1 доказываем методом Галеркина. Приближенное решение задачи (3), (4) будем искать в виде

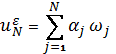
где являются собственными функциями оператора Лапласа

Система составляет базис в пространстве, ортонормированном в L₂(D), находятся из системы нелинейных алгебраических уравнений

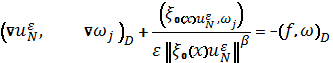,j= (10)

Уравнения (10) эквивалентны уравнениям

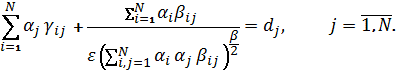(11)

где , .

Для разрешимости (11) будем использовать следующую лемму.

Лемма 1. /1/ Пусть ξ→Р(ξ) - такое непрерывное отображение R^m в себя, что для подходящего

(P(ξ), ξ) и сферы (12)

где для ξ=, мы полагаем .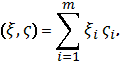

Тогда найдется такое что Р()=0, где

Ө=(), ()=.

Доказательство. (12) следует из (10). Умножим (10) на и просуммируем по j=. Далее, оценивая по неравенству Шварца, получим

(Р(),)

то есть (P(ξ), ξ), если .

Последнее условие выполняется при , где - достаточно велико. Следовательно, все условия леммы 1 о неподвижной точке выполняются. Это значит, что существует хотя бы одно решение системы уравнений (11) и для этого решения имеет место оценка

(13)

В силу данной оценки можно утверждать, что из последовательности можно выделить подпоследовательность, для которой имеют место соотношения

слабо в

в силу теоремы вложения

сильно в L₂ (D)

при N. Теперь, переходим в формуле (10) к N, ,получим интегральное тождество (8). Причем, для справедлива оценка (9). Теорема 1 доказана.

Теорема 2. Обобщенное решение задачи (3),(4) сходится к обобщенному решению задачи (1),(2) при .

Доказательство. В самом деле, в силу оценки (9) можно утверждать, что из последовательности можно выделить подпоследовательность, для которой справедливы соотношения

слабо в

сильно в L₂ (D)

при . Положим в (8) Ф Ф=0, x и переходим к пределу при получим .

Заметим при этом, что . Это следует из теоремы вложения.

при , . Таким образом, теорема 2 доказана.

Список литературы:

_{1. Кочергин В. П. Теория и метод расчета океанических течений. ВЦ СО АН СССР, «Наука», Новосибирск, 1978г., 124стр.}

_{2. Вабищевич П.Н. Метод фиктивных областей для задачи математической физики. Москва, изд. МГУ, 1991г., 156стр.}

_{3. Смагулов Ш. Метод фиктивных областей для краевой задачи уравнений Навье-Стокса. Новосибирск, 1976г., Препринт ВЦ СО АН.}