Никитин А.В., Сафонов П.А., Рашкина Н.И., Мирошниченко В.C.

             Институт Искусств и Информационных технологий, Моск. обл.

        

                                                           СВЕРТКИ

                                                                                                                                                    

         Сверткой [1] (convolution) двух функций  f (x) и g (x-u) принято называть их интегральное преобразование, в результате которого образуется третья фун- кция S(u), представляющая собой распределение одной сворачиваемой функ- ции по законам другой. В одномерном случае  формула свертки может быть записана в виде:                                                                   

                    S(u) =                   

Свертки широко используются в науке и технике. Укажем, в частности,  что важнейшая для микроэлектронной технологии информация, получаемая при обработке электронно-микроскопических снимков промышленной  про-дукции  в процессе ее изготовления (in process control) – представляет собой именно свертку точечной функции объекта (идеализированного изображения при неограниченно высоком разрешении) с т. наз. «форм-фактором» пучка электронов, сканирующих объект [2].

Свертка  также нашла применения в области изобразительных искусств, фотографии, в средствах массовой информации, на телевидении, радио – для фильтрации аудио-визуальной информации  и придания ей большей вырази-тельности и убедительности.

Особые разновидности свертки – свертки функции с самой собой, т.е.  «самосвертки» (self-convolution), именуемые «функциями Патерсона» [3] по-служили основой мощного развития современного рентгеноструктурного ана-лиза, а также используются в прецизионной метрологии малых линейных размеров [4].   По этой и другим причинам подробное изучение свойств сверток и связи этих свойств с параметрами сворачиваемых функций  представляет несомненный интерес.

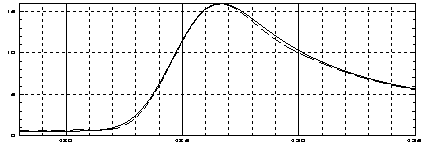
На рис.1 представлены результаты модельного эксперимента. Пусть пу-чок электронов сформирован диафрагмой с отверстием в виде правильного треугольника. Плотность потока электронов во всех точках треугольного от-верстия одинакова. Такой электронный пучок надвигается на прямолинейный край приемника электронов – цилиндра Фарадея, и частично соскальзывает внутрь него. Как будет выглядеть зависимость тока на выходе устройства от смещения диафрагмы? Конечно же, график такой зависимости окажется сверт-кой форм-факторов треугольного пучка и прямолинейной кромки приемника. Существенно, что вид выходного графика будет зависеть еще и от того, вдви-гается ли треугольный пучок вперед острием (вершиной треугольника), или в ориентации вперед донышком (основанием треугольника). Этим двум случаям соответствуют две ветви на рисунке 1.

Нижняя кривая отвечает равномерному вдвижению треугольного пучка в приемное окно детектора острым углом вперед. Верхняя кривая отображает за-висимость тока  приемника от перемещения такого же пучка, но ориентирован-ного так, чтобы треугольник вдвигался вперед одной из его сторон, а не верши-ной угла.

         Нетрудно видеть, что в обоих случаях зависимость тока приемника  от

смещения пучка выражается сверткой формы кромки цилиндра Фарадея (ее форм-фактора, которым является прямолинейный край) и форм-фактора падаю- щего пучка. Как видно из этого рисунка, зависимость результата свертки от форм-факторов сворачиваемых функций оказывается значимой, вполне от-четливой, так что подобные зависимости следует принимать во внимание. 

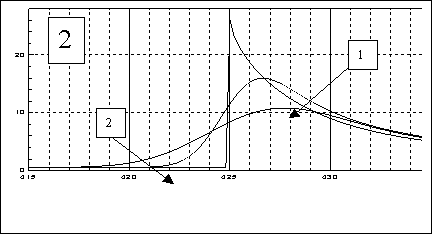
На рисунке 2 представлен еще один пример свертки, рассчитанный  как    результат математического моделирования видеосигнала в сканирующем элек-тронном микроскопе. И в этом случае видеосигнал представляет собой свертку  т. наз. точечной функции объекта K(u’) с Гауссовской функцией, описывающей распределение плотности тока по сечению пучка электронов, сканирующего объект. Объектом анализа здесь выбран край рельефного вы-ступа на плоской поверхности – типичный объект микроэлектронной технологии.

            Кривая 2 на этом рисунке отличается от кривой 1 только тем, что в этом  случае – свертывающая Гауссовская функция имела бÓльщую ширину: σ = 4 нм,  вместо  первоначальной  σ = 2 нм.

         Анализ данных этого рисунка позволяет заключить, что свертка точечной функции объекта K(u’) – (ломаная линия на рисунке) с колоколообразной гаусс-совской функцией действительно порождает свертку, которая оказывается весь-ма схожей с реальным видеосигналом, образующимся в сканирующем элект-ронном микроскопе,  как это было  продемонстрировано в [5].

  Поразительное сходство, установленное в [5],  двух кривых, одна из которых получена операцией свертки Гауссовской функции с вычисленной по теоретической модели «точечной функцией объекта» – с одной  стороны –  и реального видеосигнала, зафиксированного в промышленном сканирующем электронном микроскопе, – с другой – свидетельствует, что:

а) видеосигнал в электронном микроскопе действительно является сверткой, и б) теоретическая модель, использованная при вычислениях «точечной функцией объекта» является достаточно точной. Эти два вывода открывают пути для широкого использования математического моделирования при разработке новых методов сканирующей электронной микроскопии (СЭМ).

         Анализ рисунка 2 позволяет заключить, что свертка с Гауссовской  функ-цией (видеосигнал) заметно отличается от исходной точечной функции K(u’) по крайней мере, в двух отношениях:

1. разрешение  свертки существенно скромнее, чем разрешение K(u’), и оно снижается  по мере увеличения ширины Гауссовской кривой – σ.

2. параллельно этому, с возрастанием σ подавляются высокочастотные компо-ненты спектра K(u’), что сопровождается снижением шумов. Использование дозированного ограничения разрешения свертки используется при создании т. наз. «фильтров Гаусса» для достижения эстетических преимуществ при обра-ботке аудио-визуальной информации, а шумоподавление легло в основу па-тента США [4], используемого в промышленности.

Подпись:  

1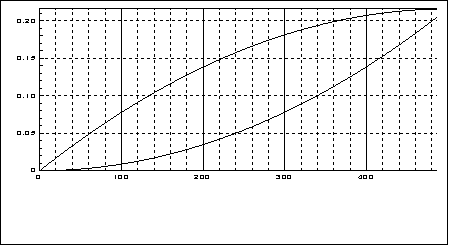
 
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


               

 

 

 

 

 

 

 

 

 

 

 

                                                                       

                                                                   Рисунки 1 и 2.

 

          В свете выводов, сделанных выше, о влияниях форм-факторов сворачива-

емых функций было бы интересно проанализировать  особенности оптических систем, например, оптических микроскопов, в  т. ч. оптических сканирующих устройств. Актуальность такого сопоставления обусловлена тем, что если в сканирующих электронных микроскопах изображение есть свертка точечной функции объекта с Гауссовой функцией: 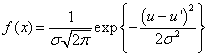,  то в оптических системах точечная функция объекта претерпевает свертку с т. наз. функцией Эйри [6], имеющей совершенно иной математический вид, а именно:   , где J1(x) – функция Бесселя 1-го рода. Функция Эйри является не более, чем «аналогом» Гауссовской функции при вычислениях изображений (сверток) в оптической микроскопии.  Это тоже колокол, но с другим масштабом по оси х. На  этом сходство этих функций заканчивается. Различия остаются. В чем они состоят?

        Отметим, прежде всего, различия в природе сигналов которые будут подвергнуты операциям свертки в рассматриваемых случаях: это либо пучки электронов, зондирующих объект изучения, с Гауссовым распределением плотности потока электронов по сечению пучка, либо потоки света, прошедшие или отраженные объектом и подвергающиеся линзовым преобразованиям. Эти преобразования в оптических устройствах производятся таким образом, что  каждая точка объекта отображается в плоскости изображения диском Эйри конечных размеров. А полное изображение предмета будет в этом случае представлять собой суперпозицию (наложение) таких дисков, порожденных каждой точкой предмета. Вот это и называется  сверткой точечной функции предмета с оптической функцией fo(x).

          Огромная разница этих двух сверток состоит в том, что разрешающие возможности любой оптической линзовой  системы оказываются на порядки ( в 30 -150 раз) скромнее разрешения электронных микроскопов. Поэтому внешнее сходство Гауссовых кривых, свойственных электронным микроскопам, и «фун-кций Эйри», характерных для оптических устройств, является иллюзией, если не принять во внимание принципиальные различия в ширине соответствующих распределений. Приведем пример. Лучшие современные оптические микроско-пы  с Цейсовской оптикой имеют разрешающую способность около 0.2 микро-ментра (200 нанометров); разрешение современных СЭМ составляет единицы или доли одного нанометра. Отношение этих рекордных величин превосходит 200 крат.  В таких же отношениях находятся и соответствующие ширины оптических и Гауссовских колоколообразных функ-ций. К дополнительным различиям можно отнести то, что Гауссовские функции монотонно спадают от единицы до нуля  при возрастании аргумента во всем диапазоне изменений его значений,  в то время как «оптические» функции являются осциллирующими (см. Рис.3). На этом рисунке представлены результаты наложения этих функций, приведенных искусственно к одному масштабу. Можно заключить, что эти функции достаточно близки по форме, несмотря на существенные различия в  их математических выражениях. Таким образом, спорным остается  вопрос: достаточно ли внешнее сходство Гауссовской и Эйри – функций (при их несомненных различиях) – для априорных заключений, что, сворачивание одной и той же точечной функции объекта с этими функциями должно привести к совпадающим, либо различающимся  результатам. Такое суждение нуждается в проверке.

         В модельном эксперименте предпринято сопоставление изображений (сверток)   одного и того же  объекта с Гауссовыми и оптическими свертыва-ющими функциями  при искусственном (возможно и не реализуемом на прак-тике) выравнивании ширины этих сворачивающих функций.

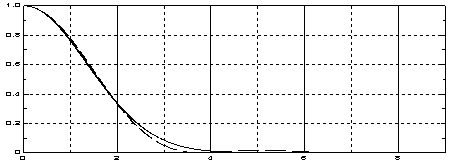
На рисунке 4 представлены наложенные свертки точечной функции объ-екта – той же самой, K(u’), что  использовалась при вычислении видеосигналов, представленных на рисунке 2, – с Гауссовской функцией и функцией Эйри.

  

4
 
                                         

                                                                      Рисунки 3 и 4.

Видно, что свертки функции объекта с двумя математически различными функциями – Гауссовской и Эйри-функцией при их одинаковой ширине оказы-ваются почти неразличимыми. Подробный численный анализ выявил некото-рые несущественные, но характерные различия. Так, на координатах u = 421 нм, (в области, выделенной овалом)  можно обнаружить локальный максимум свертки с функцией Эйри, отсутствующий на свертке с Гауссом. Природа появления этого  «сателлита» вполне понятна, если учесть, что сама функция Эйри имеет локальный побочный максимум на Х ≈ 5.1. В самом деле: когда середина функции Эйри располагается в окрестностях значения u=420, то ее сателлит попадает на u=420 + 5.1= 425.1, а это как раз и есть зона максимума K(u’). Так что появление этого сателлита, и именно на таком расстоянии от главного максимума, было вполне ожидаемым и теперь подтверждено расче-тами. В остальном свертка точечной функции объекта с Гауссовской функцией, либо с оптической функцией Эйри – различаются несущественно и  практи- чески совпадают.                                     

 

 

 

 

 

 Литература.

1. Wikipedia

 2. Амосов Р. М., Кузнецова В. В., Никитин А. В. “Характеристики потока вторичных электронов, формирующих видеосигнал в РЭМ”, // Электронная техника. Сер. 3. Микроэлектроника. 1982,.Вып. 5–6. С. 43–49.

 3. Липсон Г,. Кокрен В. «Определение структуры кристаллов»,  М.– ИЛ, 1956, 415с.

 4. Патент США  № 6.664.532  от 16 Дек. 2003 г.,

 5. Nikitin А. V. “Use  of  Mathematical Modeling for Measurements  of Nanodimensions in Miсro- electron  Nanometrology”,  Measurement Techniques, Vol. 54, No. 12, March, 2012, pp. 1346-1352.    

 6.  М.Борн, Э. Вольф “ Основы оптики“, М, Наука, 1973,  720 с.