Современные информационные технологии

УДК 519.6 (075.8)

Галагузова Т.А., Ескен С., Карих М.

Таразский инновационно-гуманитарный университет, Тараз, Казахстан

Использование EXCEL в преподаваниИ математики

Появление и бурное развитие электронной вычислительной техники (ЭВМ) значительно увеличили масштабы и ускорили темпы внедрения статистических методов анализа данных в практику научных исследований

Использование ПК для обработки данных стало особенно эффективным с появлением электронных таблиц – пакетов прикладных программ для автоматизации табличных расчетов, а именно табличного процессора Excel, ставшего к тому времени довольно мощным инструментом для проведения инженерных и научных расчетов.

Благодаря этим таблицам многие сложные статистические методы, доступные ранее лишь узкому кругу профессионалов-математиков, стали доступны широкому кругу пользователей прикладников [1].

В последние годы наметилась устойчивая тенденция к внедрению компьютерных технологий в процесс преподавания математических дисциплин (в том числе «Теории вероятностей и математической статистики»).

Excel как нельзя лучше подходит для этой цели. Выполняя статистический анализ на рабочих листах этого рабочего процессора, можно видеть все его этапы, что делает анализ данных более наглядным и понятным. Это сделало Excel отличным средством обучения [2].

Работа с данными, графиками и текстами стала выполняться почти так же, как в других приложениях Windows, входящих в комплекс программ Microsoft Office.

В среде Excel можно освоить технологию статистического анализа данных и использовать ее в своей практической деятельности. Среда Excel предназначена для специалистов-практиков, применяющих в своей работе методы математической статистики: медиков, биологов, социологов, экономистов, инженеров, научных работников, студентов, аспирантов и преподавателей [3].

В качестве примера расчетов в Excel рассмотрим решение обыкновенных дифференциальных уравнений - популярный раздел математической дисциплины «Численные методы».

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). В основе метода ломанных Эйлера лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме. Идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление».

Пусть требуется найти на отрезке [a,b] решение обыкновенного дифференциального уравнения y’=f(x,y) при заданном начальном условии y(a)=y₀.

Решить численным методом - это значит для заданной последовательности аргументов

х₀, х₁…, х_n и числа у₀, не определяя функцию у=F(x),

найти такие значения у₁, у₂,…, у_n, что у_i=F(x_i) (i=1,2,…, n) и F(x₀)=y₀.

Таким образом, численные методы позволяют вместо нахождения функции y=F(x) получить таблицу значений этой функции для заданной последовательности аргументов.

Величина h=x_k-x_k-1 называется шагом интегрирования [4].

Приближенное значение решения уравнения в точке у₁, можно определить по формуле Общая итерационная формула метода Эйлера имеет вид

Задание. Используя метод Эйлера, найти решение дифференциального уравнения у'=x²+у² при начальных условиях:

x₀= 0, y(x_о) = -1, c шагом h = 0,1 на интервале [0, 1].

Для практического решения задачи введем исходные данные: отрезок интегрирования заносим в ячейки (А4:В4); начальное значение у₀ в ячейку (С4); количество отрезков разбиения в ячейку (D4); формулу расчета шага интегрирования h в ячейку (E4) (см.рис.2).

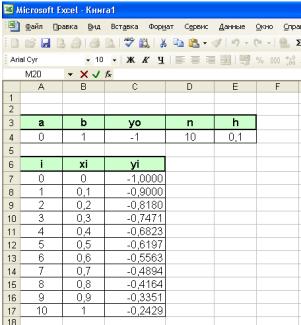
Рис.2. Численное решение дифференциального

уравнения методом Эйлера.

В блоке (А7:А17) указываются номера итераций; в блоке (В7:В17) рассчитываются точки разбиения отрезка интегрирования; в ячейках (С7:С17) реализуется формула метода Эйлера Изобразим полученные значения приближенного решения на графике, используя точечный тип диаграммы (см.рис.3).

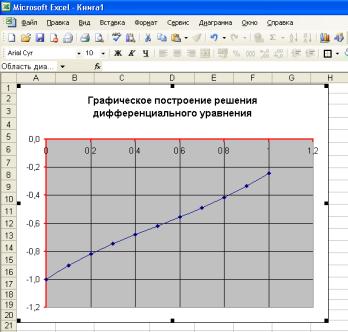
Рис.3. Приближенное решение, полученное методом Эйлера.

Результат есть ломаная, дающая приближенный вид интегральной кривой – графика решения дифференциального уравнения при заданном начальном условии.

Список использованной литературы

1. Вадзинский Р. Статистические вычисления в среде Excel. Библиотека пользователя. – СПб.: Питер, 2008. – 608 с.:ил. – (Серия «Библиотека пользователя»).

2. Финансово-экономические расчёты в EXCEL. Издание 3-е, переработанное и дополненное./ Овчаренко Е.К., Ильина О.П., Балыбердин Е.В. – М.: Информационно-издательский дом «Филинъ», 1999. – 328 с.

3. Microsoft EXCEL. Электронные таблицы и базы данных в задачах. / Нечаев В.М. – М.: Интеллект-Центр. 2001. – 96 с.

4. Численные методы и их реализация в Microsoft Excel. Ч.2.: лабораторный практикум по информатике / Сост. Е.В. Башкинова, Г.Ф. Егорова, А.А. Заусаев. – Самара; Самар. гос. техн. ун-т, 2009, 44 с.