СТАТИСТИЧЕСКАЯ ТЕОРИЯ ФАЗОВОГО ПЕРЕХОДА ТИПА ПОРЯДОК–БЕСПОРЯДОК В СМЕСИ ФТОРФУЛЛЕРЕНОВ

В широких экспериментальных и теоретических исследованиях физико-химических и термодинамических свойств фторфуллеренов Ф₁=C₆₀F₄₈, Ф₂=C₆₀F₃₆ и им подобных, проводимых в последние годы, изучается, в частности, их структура, фазовые превращения и теплоемкость [1-3].

Экспериментальное исследование темплоемкости С_Р фторфуллерена Ф₁ выявило аномалию в ее температурной зависимости: в области температур Т₀~ 330 К на кривой С_Р(Т) появляется пик [2]. Определение кристаллической и молекулярной структуры конденсата показало, что при этой температуре происходит фазовый переход типа порядок–беспорядок. Структура фторфуллерита изменяется от упорядоченной объемноцентрированной тетрагональной (ОЦТ) в неупорядоченную гранецентрированную кубическую (ГЦК) [1,3]. При этой же температуре наблюдается аномальное изменение параметра решетки [3], по-видимому, обусловленное реализацией фазового перехода.

Представляет интерес теоретическое исследование фторфуллеренов, разработка статистической теории фазового перехода при температуре Т₀, построение диаграммы состояния системы, выяснение температурной зависимости теплоемкости фторфуллерита, объяснение и обоснование появления возможной аномалии в этой зависимости при температуре Т₀.

Для решения поставленной задачи рассчитывалась свободная энергия конденсата. В теоретических расчетах рассматривалась смесь фторфуллеренов Ф₁, Ф₂, которая, согласно экспериментальным данным, ниже температуры Т₀обладает упорядоченной ОЦТ кристаллической решеткой, а выше температуры Т₀– неупорядоченной ГЦК решеткой. В расчетах использовался метод средних энергий [4], приближение учета энергий взаимодействия ближайших фторфуллереновых пар и модель сферически симметричных жестких шаров [4,5].

Расчет свободных энергий ОЦТ и ГЦК фаз проводился с использованием известной формулы , где i = 1, 2 для ОЦТ и ГЦК фаз, E_i – внутренняя конфигурационная энергия, равная сумме энергий парного взаимодействия ближайших фторфуллеренов, G_i – термодинамическая вероятность, определяемая количеством различимых распределений фторфуллереновых молекул по всем их позициям, k– постоянная Больцмана, T– абсолютная температура [6].

Вычисление свободных энергий в расчете на один узел кристаллической решетки и в приближении квадратичной зависимости энергии упорядочения ОЦТ фазы от параметра порядка дало такие результаты:

, (1)

, (2)

где N – число всех узлов (фторфуллеренов) кристалла, η – параметр порядка в распределении фторфуллеренов Ф₁, Ф₂ по узлам ОЦТ решетки, е₁, е₂ – слагаемые свободных энергий, не зависящие от параметра порядка, ω₁ – постоянное слагаемое энергии упорядочения ОЦТ фазы,

, (3)

, (4)

с₁, с₂ – концентрации фторфуллеренов Ф₁, Ф₂.

Формулы (1) – (4) определяют зависимость свободных энергий f₁, f₂ от температуры Т, состава фаз (концентраций с₁, с₂), параметра порядка η и энергетических констант е₁, е₂, ω₁.

Фазовое превращение ОЦТ→ГЦК происходит при температуре Т = Т₀ (фазовый переход первого рода), когда свободные энергии обеих фаз равны f₁ = f₂.

Равновесное значение параметра порядка зависит от температуры, концентраций с₁, с₂ и константы α.

Для ОЦТ фазы стехиометрического состава уравнение термодинамического равновесия приобретает вид

. (5)

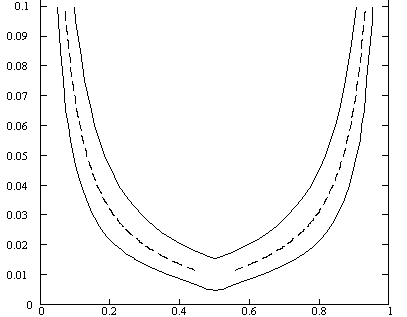
На рисунке приведена диаграмма состояния системы, построенная с использованием как метода общих касательных к кривым f₁(c₁), f₂(c₁), так и по точкам пересечения этих кривых.

kT, эВ

ГЦК

ОЦТ+

ОЦТ ГЦК

c₁

Диаграмма состояния молекулярных фторфуллереновых кристаллов,

построенная по методу общих касательных кривых свободных энергий

f₁(c₁), f₂(c₁) фаз ОЦТ и ГЦК (сплошные кривые) и по точкам пересечения

этих кривых (пунктирная кривая), построенных для разных температур

Видно, что при низких температурах из смеси фторфуллеренов Ф₁, Ф₂должна реализовываться в соответствии с экспериментальными данными упорядоченная ОЦТ фаза. С повышением температуры происходит фазовый переход в неупорядоченное состояние смеси Ф₁, Ф₂ с ГЦК решеткой, что также соответствует экспериментальным данным. С ростом температуры расширяется концентрационный интервал формирования ГЦК фазы, и при достаточно высоких температурах почти во всем концентрационном интервале реализуется ГЦК фаза. Существование ОЦТ фазы сохраняется и при достаточно высоких температурах, но для малых или больших концентраций фторфуллеренов Ф₁, Ф₂. В области вблизи стехиометрического состава реализуется ГЦК фаза в широком температурном интервале, начиная от kT₀ 0.04 эВ. Двухфазные области формирования ОЦТ и ГЦК фаз начинают проявляться при kT₀≈ 0.005 эВ для системы стехиометрического состава, которые далее расширяются с повышением температуры до kT ≈ 0.02 эВ. Дальнейшее повышение температуры смещает двухфазные области смеси ОЦТ+ГКЦ фаз в сторону увеличения и уменьшения концентрации с₁, и эти области сужаются.

Разработанная статистическая теория позволила обосновать и объяснить фазовый переход типа порядок–беспорядок в смеси фторфуллеренов Ф₁=C₆₀F₄₈, Ф₂=C₆₀F₃₆, наблюдаемый экспериментально при температуре 330К, когда реализуется переход из упорядоченной ОЦТ фазы в неупорядоченную ГЦК фазу.

Литература

1. Crystal structures of the fluorinated fullerenes C60F36 and C60F48 / S. Kawasaki, T.Aketa, H.Touhara, F.Okino, O.V.Boltalina, I.V.Gol'dt, S.I.Troyanov, R.Taylor // J. Phys. Chem. B. – 1999. – V.103(8). – P.1223-1225.

2. The low temperature heat capacities of fluorofullerenes / A.I. Druzhinina, N.A.Galeva, R.M.Varushchenko, O.V.Boltalina, L.N.Sidorov // J. Chem. Thermod. – 1999. – V.31(11). – P.1469-1482.

3. Kawasaki S. Crystal structures and phase transformations of the fluorinated fullerenes / S. Kawasaki, F.Okino, H.Touhara // Mol. Cryst. Liq. Cryst. – 2000. – V. 340. - P.629-633.

4. Матысина З.А. Порядки различного типа в кристаллах и фазовые превращения в углеродных материалах / З.А.Матысина, С.Ю.Загинайченко, Д.В.Щур. – Днепропетровск: Наука и образование, 2005. – 524 с.

5. Матысина З.А. Углеродные наноматериалы и фазовые превращения в них / З.А.Матысина, С.Ю.Загинайченко, Д.В.Щур. – Днепропетровск: Наука и образование, 2007. – 680 с.

6. Смирнов А. А. Молекулярно-кинетическая теория металлов – М., 1966. – 488 с.