Физическая кульутра и спорт / 1. Физическая культура и
спорт: проблемы, исследования, предложения.
Пугач Я.И.
Харьковская
государственная академия физической культуры, Украина
Основные положения
построения семантических пространств для упорядоченного представления
результатов исследований
Аннотация: Рассмотрены положения о
построении семантических пространств, необходимых для упорядоченного
представления эмпирических материалов исследования. Раскрываются особенности
структуры введения измерений в трехмерном ортогональном пространстве,
представленном единичным кубом с плотностью распределения его содержания,
соответствующего «нормальному закону». Введение сигмальной меры в этом
пространстве порождает представление различных эквипотенциальных состояний, как
поверхности пяти правильных многогранников вложенных в единый куб. Это дает
возможность проведения аналитического исследования основанного на
математических свойствах полученных геометрических построений, что обеспечивает
новый подход в исследовании морфо-функциональных процессов в описании
адаптационных процессов. Возможности данного метода существенно расширяют
границы исследования этих процессов за пределы, доступные при использовании
прямых эмпирических методов. Представленные данные описаны впервые.
Ключевые слова: семантические
пространства, правильные многогранники, размерность пространства,
статистический принцип, дихотомия, толерантность.
Введение: Олимпийские игры
являются высшим уровнем спортивных соревнований. Достижение успехов в них и
даже участия требуют длительной и кропотливой подготовки спортсмена. Успех в
этом процессе достигается не только одаренностью спортсмена и опытностью
тренера, но и сложными научными поисками, которые обеспечивают построения
наиболее оптимальных режимов организации тренировочного процесса.
В системе олимпийского
образования раздел научного обеспечения построения тренировочного процесса,
основанного на учете индивидуальных норм
физического и психического развития, уровня физической подготовленности
и текущего функционального состояния – является необходимым звеном его
структуры. В свою очередь, любые научные исследования достигают необходимого
успеха при наличии соответствующих методов исследования и правильного
представления полученных результатов, что возможно только при наличии
соотвутсвующих пространств для упорядоченного их представления.
Цель: построение
семантических пространств для упорядоченного предствления эмпирических данных.
Задача: Определить структуру
построения семантического пространства единичного куба «с нормальной
плотностью» распределения его элементов.
Состояние
вопроса: Развитие
науки определяется используемыми методами исследований. На каждом этапе
развития, достигнув пределов своих возможностей, продолжение исследований
является бесплодным занятием и не приносит новых научных результатов.
Дальнейшее продвижение требует новых более точных и содержательных методов
исследований. [6,15]
Наличие компьютерных технологий, программного
обеспечения открыли возможности широкого использования методов математического
моделирования и их дальнейшей разработки. [12,13]
Проведение исследований в любой области знаний
предполагает поиск определённого порядка отношений, в основе которых лежат
скрытые закономерности. Для упорядочивания представлений каких-либо характеристик
или смыслообразующих понятий необходимо построение соответствующих
семантических пространств, которые основаны на геометрических правилах
использования измерительных шкал. [1,2]
Основные требования к построению шкал, по
которым оцениваются измеряемые характеристики исследуемых процессов или
явлений, состоят во введении в них единицы измерения. В практике проводимых
исследований используются четыре вида шкал: шкала наименований, порядковые
шкалы, шкала интервалов, шкала отношений. [4,7] Применение какой либо из
отмеченных шкал определяется сутью измеряемых элементов и толерантностью
пространств измеряемых характеристик. Соизмеримость толерантности пространств
является обязательным требованием в проводимых исследованиях в любой области
знаний. [8,9]
Измерительные шкалы, которые используются, как
координатные оси должны быть независимыми, что обеспечивает их ортогональность
при построении семантических пространств. При использовании различных
независимых шкал необходимо обеспечить соизмеримость их масштабов так, чтобы
отношение единиц масштабов измерения равнялось единице.
Единица, какой бы она не казалась постоянной
сама себе, содержит в себе бесконечную разнообразность, потому что она может
быть нулевой степенью любого иного числа. Ноль, в свою очередь, богаче по
содержанию, нежели любое иное число. [10,11]
Эти свойства единицы и нуля широко используются
в преобразованиях семантических пространств, при переходе из одной системы
координат в другую, при объединении пространств, когда элементы одного пространства
как исходные упорядоченные характеристики выступают стандартом для сравнения
упорядоченности аналогичных характеристик другого пространства.
Такой стандарт представляет структуру условной
средней величины, которая может выступать началом отсчёта при осуществлении
сравнения и играть роль нуля как начала отсчёта отклонений сравниваемых
величин. При сравнении взаимного противодействия двух величин результат их
превосходства может быть равен нулю, а степень напряжения может достигать
любого возможного значения. В этом случае их отношение развитого напряжения
равно единице, а превосходство противостояния равно нулю.
Изложенные положения наблюдаются в пространствах
любой размерности. При рассмотрении структуры одномерного пространства, шкала
измерений происходящих взаимодействий основана на дихотомическом принципе
строения их отношений. В линейных одномерных пространствах в шкалах вводится
порядок следования элементов, а сама шкала, в зависимости от требуемой точности
измерения расположения порядка следования элементов, разбивается на необходимое
число равных интервалов. В этом случае можно говорить об измерении плотности
распределения элементов, скопляемых в соответствующем участке шкалы, в котором измеряется
исследуемый признак. Для установления закономерности наблюдаемого распределения
элементов с измеряемым признаком необходимо двухмерное линейное пространство, в
котором второй независимой, ортогонально расположенной с равномерным масштабом
измерения выступает шкала количественного измерения элементов
с наличием исследуемого
признака.
Такое представление измеряемой характеристики
исследуемого признака даёт графическое отображение его приращения по мере
увеличения проявляемого значения от минимально доступного для регистрации до
максимально встречаемого. В таком пространстве можно получить структуру
плотности распределения контролируемого признака, в нём каждая контролируемая
величина имеет порядковый номер в ранге величины измеряемого признака и
количество его встречаемости.
Для представления полной характеристики
структуры распределения признака в двухмерном ортогональном линейном
пространстве необходимо добавить третью независимую ортогональную шкалу
измерения, отражающую порядок появления элементов встречающегося ранга
измеряемого признака. Это трехмерное пространство позволяет говорить не только
о ранге встречающегося в исследовании
признака, но и порядка его наблюдения, одновременного или последовательного
проявления, что позволяет видеть амплитудно-временную характеристику его
поведения.
Такое трёхмерное пространство можно представить
в виде единичного куба, в котором каждая из ортогональных шкал может быть
выражена как единица, соответствующая диапазону встречающихся значений от его
минимума до максимума. Объединяя все начальные значения (минимумы) в начало
отсчёта, им можно присвоить значение нуля. Либо за ноль можно принять середину
каждой из исследуемых шкал. Тогда крайним значениям можно присвоить
величины -1 и 1. Любое отклонение от
середины отражается соответственно со знаком + или -, что представлено на
рисунке 1.
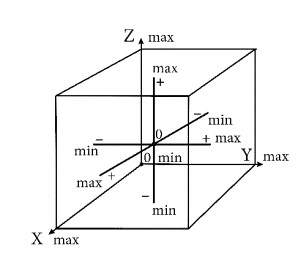
Рис. 1. Трехмерное пространство отражения ранга
наблюдаемых элементов и порядка их основания.
Особенностью построения шкалы одномерного
линейного пространства является дихотомический характер ее структуры. В таком
случае объединение двух шкал, находящихся в дихотомическом взаимодействии в
одну отражает долевое участие в
определении результата и взаимодействия в получении конечного результата. Если
каждый из элементов такого рода дихотомии обозначить через символ (р) и (q),
то всегда выполняется условие формирования масштаба как 1 ≥ |р – q| ≥ 0, так как и (р) и (q)
изменяют своё значение от 0 до 1 с взаимопротивоположным знаком.
Равным образом их можно разместить так, чтобы
начало отсчёта каждой шкалы дихотомий совпадали, но в этом случае не будет
учтена мера напряжения борьбы и единства противоположностей. Для получения
этого результата в графическом представлении необходимо воспользоваться
двухмерным ортогональным линейным пространством, в котором образующими
выступают выбранные дихотомии. В этом случае биссектриса координатного угла
выступает шкалой их напряжения, при котором его отношение равно единице, а мера
превосходства – нулю. Данное описание представлено на рис.2.
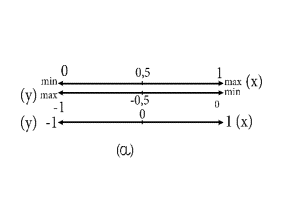
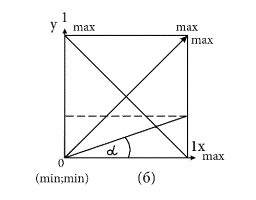
Рис.2 Построение дихотономической шкалы измерения
меры присутствия признака (a) и отношения равной
напряженности, обеспечивающие равновесное состояние (б)
В силу того, что представленное двухмерное
пространство является единичным квадратом, его диагонали несут разное смысловое
содержание оценки результата дихотомических отношений. Одна из них является
мерой равной напряженности, а вторая мерой превосходящей напряженности одной из
составляющей дихотомические отношения. Во всех случаях эта характеристика
измеряется (tg ![]() ), где
), где ![]() является углом
наклона прямой, соединяющей точку данного пространства, принадлежащие этой
прямой.
является углом
наклона прямой, соединяющей точку данного пространства, принадлежащие этой
прямой.
Если оценивать частоту встречаемости различных
состояний напряжения в представленном семантическом пространстве в соответствии
с упорядоченным их рангом по величине проявления, то наиболее устойчивая
структура такого рода отношений по направлению каждой из диагоналей будет
представлена нормальным законом распределения.
Введение третьего измерения, отражающего порядок
встречаемости конкретного состояния напряжения или продолжительность проявления
в порядке своей встречаемости, позволяет этой шкале измерения также отмечать
наиболее устойчивое равновесное состояние, которое будет описываться нормальным
законом распределения. Трёхмерное семантическое пространство упорядоченного
представления оцениваемого режима проявления определённого фактора можно
представить как единичный куб с нормальной плотностью распределения
упорядоченного множества контролируемой характеристики состояния его
проявления.
Особенностью построения трёхмерного пространства
в отличие от двухмерного состоит в том, что оно может иметь две формы его
представления, каждая из которых содержит различное семантическое и структурное
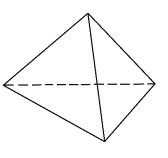
представление (рис. 3).
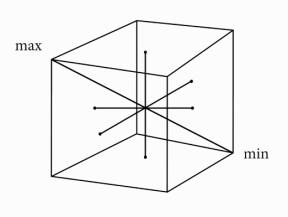 а
а 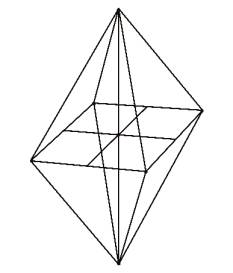 б
б
Рис. 3 Трехмерное семантическое пространство
упорядоченного представления долевого участия контролируемых характеристик (а)
– куб, (б) – октаэдр
В одном случае это единичный куб, а в другом
октаэдр. Отличительная сторона строения семантического пространства, представленного
кубом, состоит в том, что у него только одна из четырёх диагоналей может
выступать как обобщающая шкала, которая несёт в себе равновозможные результаты
совокупности точек, отражающих одинаковый конечный результат, полученный при
разном значении долевого участия независимых образующих это пространство.
Фактически эта диагональ несёт в себе
статистическое обобщение эквифинальных результатов взаимообусловленных
отношений независимых образующих и выступает шкалой их представления. Данная
шкала выступает как независимая дихотомическая структура, обеспечивающая
понижение размерности пространств из трёхмерного в одномерное. Эти преобразования
можно осуществлять в обе стороны, изменяя тем самым размерность пространства
построения и организации исследуемого явления или протекаемого процесса.
В таком преобразовании проявляются принципы
изоморфизма, инвариантности и статистического обеспечения эквифинального
результата. На каждом уровне организации сохраняется трёхмерность построения
пространства, в котором каждая независимая координата, в свою очередь, является
обобщающей характеристикой трёх независимых координат предшествующего уровня
организации жизнеспособных отношений.
На всех уровнях организации жизнеспособных
отношений могут участвовать только независимые (ортогональные) переменные. На
каждом уровне организации из обобщающих диагоналей, отражающих эквифинальный
статистический результат взаимообусловленных отношений, строится новый уровень
организации, включающий все предшествующие. Среди всевозможных вариантов
независимых переменных исключаются те, у которых на предшествующих уровнях
встречаются одинаковые переменные (при этом утрачивается ортогональность). Этот
факт уменьшает число возможных вариаций их сочетаний при построении
жизнеспособных взаимообусловленных отношений
в структуре систем, сокращая ее жизнеспособность. В зависимости от уровня
совпадений зависимых переменных, это приводит к накоплению ошибок в процессе
регенерации (ремонтопригодности) элементов рассматриваемой системы.
Следовательно, одно из определяющих положений
построения семантических пространств является использование независимых
ортогональных характеристик, которые выступают координатными осями.
Использование тех же независимых ортогональных
измерительных шкал, что и при построении единичного куба, но для построения
октаэдра позволяет сформировать иную структуру пространства с позиции
геометрического представления. Естественно возникает и другая семантика.
Особенность такого преобразования состоит, прежде всего, в том, что те же три
ортогональные друг к другу плоскости, которые лежат в основе построения куба
размещаются ортогонально друг к другу, но не по координатным осям, а по
обобщающим диагоналям, которые выступают в данном случае координатными осями.
При таком построении каждая координатная ось представляется двумя диагоналями
из разных координатных плоскостей куба. Из шести плоскостных диагоналей
формируется три по две объединенные координатные оси. В октаэдре нет обобщающей
диагонали. В отличие от куба эти плоскостные диагонали имеют ортогональное
расположение друг к другу, что и определяет иную семантику порождающих
отношений, которая заключается в отражении меры напряженности в сохранении
различных равновесных жизнеспособных состояний.
Данные пространства имеют строгую природу
совмещения октаэдра в куб и куба в октаэдр. Однако на основе базисных
характеристик куба, которыми выступают три независимые координатные оси и шесть
диагоналей координатных плоскостей строятся различные октаэдры.
Октаэдр, построенный на координатных осях своими
координатными плоскостями, развёрнут на угол ![]() (45˚) и каждые
противолежащие грани оказываются перпендикулярными диагоналями вершин куба. При
этом каждые две грани октаэдра, пересекая соответствующую диагональ вершин
куба, делят её на три равные части.
(45˚) и каждые
противолежащие грани оказываются перпендикулярными диагоналями вершин куба. При
этом каждые две грани октаэдра, пересекая соответствующую диагональ вершин
куба, делят её на три равные части.
В данном случае представляет интерес рассмотреть
все перпендикулярно проведённые плоскости через точки, составляющие одну шестую
длины диагонали вершин единого куба и границы их проекций друг на друга, а
также области (многогранники), которые они образуют в пространстве единичного
куба при пересечении их каждой из четырёх диагоналей вершин единичного куба.
Особенности построения этих геометрических поверхностей состоят в том, что они
имеют общий центр начала отсчёта и общие независимые базовые координатные
характеристики.
Второй октаэдр, который строится на базе
диагоналей координатных плоскостей, также сохраняет единый центр начала отсчёта
и включает в себя независимые базовые характеристики, но имеет принципиально
иное семантическое содержание и с единичным кубом образуют невыпуклые формы. [14,17]
В зависимости от способа построения октаэдра
определяется содержание его семантического пространства. Если в кубе все концы
координатных осей соединить, то образовавшиеся грани определяют объемную
фигуру, которой является октаэдр. В этом случае противоположные грани
пересекают под прямым углом диагонали, соединяющие противоположные вершины
куба. Если диагонали разбить на шесть равных частей, то каждая грань проходит
через точку диагонали, отстоящую от центра системы координат ровно на 1/6 всей
ее длины.
Необходимо отметить, что построение октаэдра на
базе единичного куба может быть осуществлено последовательного, либо как
вписанного в куб, либо куба вписанного в октаэдр. В любом случае через точки
соприкосновения этих трехмерных образований можно описать сферу, которая
разделяет их. Такую операцию последовательного вложения можно осуществлять
неограниченное число раз.
Каждый последовательный шаг
поворачивает систему координат на 45° ![]() , при этом радиус сферы, разделяющей границы между кубом и
октаэдром увеличивается по закону логарифмической спирали, отражая дискретный
рост единицы измерения шкал на каждом этапе развития системы
взаимообусловленных отношений самоорганизующихся процессов.
, при этом радиус сферы, разделяющей границы между кубом и
октаэдром увеличивается по закону логарифмической спирали, отражая дискретный
рост единицы измерения шкал на каждом этапе развития системы
взаимообусловленных отношений самоорганизующихся процессов.
Введение на всех координатных осях масштаба
меры, построенной на основе нормального закона плотности распределения
отклонений от ожидаемого результата позволяет во всем измеряемом пространстве
ввести меру в долях сигмальных (s) отклонений.[3,9] В
зависимости от потребности определения границ зон с необходимой плотностью
распределения показателей контролируемого результата, при проведении секущих
плоскостей через соответствующие точки на измерительных шкалах образуются все 5
правильных многогранников. [15,16,18,19] Это в существенной мере определяет
природу их возникновения как зон эквифинального раздела результатов
взаимообусловленного отношения образующих факторов (первоэлементов), которые
определяют уровни жизнеспособности целостной системы. (рис. 4)
 1
1 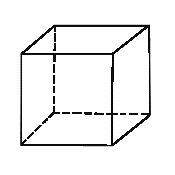 2
2 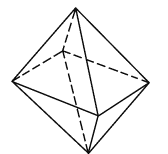 3
3
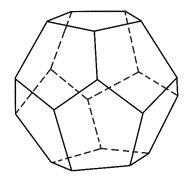 4
4 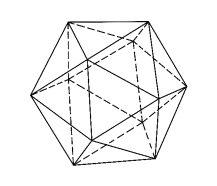 5
5
Рис. Правильные многогранники, которые отражают
зоны эквифинального результата взаимообусловленных отношений, определяющих жизнеспособность целостной системы,
возникающие при введении нормального закона плотности распределения
контролируемых характеристик в данном кубе, измеряемые в долях сигмального
отклонения.
1 – тетраэдр, 2 – куб, 3 – октаэдр, 4 – дедекаэдр, 5 – икосаэдр.
Имея данный центр пересечения координатных осей
эти многогранники вписаны в единичном кубе и разделены сферами.
Заключение
Относительно каждого из правильных
многогранников – тетраэдра, октаэдра,
икасаэдра, куба (гексаэдра), додекаэдра при их вложении друг в друга
можно провести разделяющие и сферы как это было описано для куба и октаэдра.
Каждый из многогранников имеет свой порядок последовательного включения друг в
друга. После завершения цикла он повторяется в том же порядке. Такая процедура
осуществляется в обоих направлениях – сжатии и расширении размера пространства.
В каждом конкретном случае рассматриваемая сущность исследуемых процессов может
носить различный характер.
При построении правильных многогранников
существенную роль в трактовке смыслового содержания полученного семантического
пространства играют выбранные системы координат. Они в исходном построении
являются общими для куба и октаэдра или октаэдр строится на базе обобщающий
диагоналей координатных плоскостей куба.
Описанные построения семантических пространств
отражают застывший статический характер сложившихся равновесных отношений. В
действительности, каждая взаимодействующая, составляющая целостную структуру
системы, имеет диапазон вариации, который обеспечивает процесс ее адаптации в
их совместном поведении.
Исследования динамики этих процессов в описанных
семантических пространствах позволяют наблюдать закономерности и их протекания,
а на их основании формировать математические модели, которые используются как
метод более углубленного изучения процессов адаптационного поведения,
недоступного для наблюдения при
проведении прямых эмпирических опытов.
Данные результаты геометрического построения и
анализа взаимосвязи эквипотенциальных состояний во взаимообусловленных
отношениях целостной системы, описанных пятью правильными многогранниками,
представленными в единичном кубе, с введенной плотностью наблюдаемых процессов,
которые подчиняются нормальному закону распределения - получены и приведены
впервые.
Литература:
1.
Аристотель.
Сочинения в 4-х т. М. 1978. Т.2.
2.
Берже
М. Геометрия т.1. М. Мир. 1984. С.38-44, 479-504.
3.
Бондаревский
В.П. Статистическое распределение студентов «Теория и практика физической
культуры» 1975, №5, С 55 - 54
4.
Бурлачук
Л.Ф., Морозов С.М. Словарь справочник по психологической диагностике. Киев «Думка» 1989. С.162-163.
5.
Вейль
Г., Симметрия – М. «Наука». 1968, с.101
6.
Гикка М. Эстетика пропорций в природе и искусстве М. «Всесоюзная
Академия архитектуры» 1936, с. 310
7.
Гильберт
Д., Кон-Фосен С. Наглядная геометрия. М. Наука. 1981. С.40-101.
8.
Горбань
А.Н., Хлебопрос Р.Г. Демон Дарвина. Идеи оптимальности и её естественный отбор.
М. «Наука». 1988. С.19-65
9.
Зациорский
В.М. Спортивная метрология. М. «Физк.
и спорт». 1982. С.10-14.
10.
Короленко А.А., Петленко В.П. Философские
проблемы теории нормы в биологии и медицине. М. «Медицина». 1977. С.5-6.
11.
Кофман. А. Введение в теорию нечетких
множеств. М. «Радиосвязь » 1982, С432.
12.
Лебег А. Об измерении величин. М. 1960.
13.
Левмтин
К. Геометрическая рапсодия. М. 1976.
14.
К. Математические рукописи. М. «Полит. издат.» 1968.
15.
Смирнов
Н.В., Дунин – Барковский И.В. «Курс теории вероятности и математической
статистики для технических приложений» - М. «Наука» 1965, с.512.
16.
Хьюзмоллер Д. Расслоение пространства – М.
«Мир» 1970 с.54-71
17.
Ягер Р.Р. Нечёткие множества и теория
возможностей, последние достижения. М. «Радио и связь». 1986. С.408.
18.
Coxeter H.S.M. Regular Polytopes –
Methuen 1968 p.13
19.
Fejes – TOTH L Regular Figures – Peragamon 1969, p.120-121