Строительство и архитектура
/3. Современные технологии в строительстве,
реконструкции и реставрации
К.т.н., докторант Дадар А.Х.
Тувинский государственный университет,
Россия, Республика Тыва
Об оптимизации очереди реконструируемых объектов на
базе генетического алгоритма и статистического поиска доминантных фрагментов
В современном строительстве большую долю составляют объекты, на которых
проводятся работы, связанные с реконструкцией, санацией, техническим ремонтом и
др. аналогичными видами строительства [1, 2]. Для перечисленных объектов
имеется определенная специфика, связанная с тем, что продолжительности,
стоимости и объемы работ на них значительно меньше соответствующих
характеристик работ, выполняемых на объектах нового строительства. Из этого следует,
что даже для сравнительно непродолжительного горизонта планирования (например,
в один год) очередность строительства будет исчисляться десятками объектов. Таким
образом, задача поточного строительства, ориентированная на поиск оптимальной
очередности освоения объектов, изложенная в работе [3], продолжает оставаться
актуальной и в настоящее время.
По принятой в научной литературе классификации, подобные задачи относят к
категории NP-трудных, что определяет экспоненциальное увеличение их вычислительной трудоемкости
в зависимости от линейного увеличения числа объектов в очереди [4]. Если на
возможные перестановки объектов в очереди не накладывают ограничений, то для
числа объектов N затраты времени на вычисление всех вариантов очередности будет определяться
формулой Q=a∙N!, в которой a – это время
затрачиваемое на расчет одного варианта перестановки объектов. Например, для решения
задачи оптимизации очередности реконструкции энергоресурсосберегающих объектов,
представленног в работе [5], на расчет каждого варианта, осуществленного в
программе управления проектами типа Microsoft Project, требовалось время равное ≈0,001с. Из этого следует, что для полного перебора всех вариантов
комплекса, состоящего из 10-ти объектов, необходимое время расчета составляет
более 3,6∙103с.
(один час), а если решать задачу с 20-ю объектами, то полное время расчета составит
более 1012 часов, то есть расчет будет исчисляться годами.
Рассмотрим, какие организационно-технологические условия могут уменьшить
размерность представленной задачи. В качестве первого мероприятия может быть
рекомендован учет ограничений на последовательность освоения объектов,
описанный в работе [6] на примере анализа формирования
организационно-технологической схемы застройки селитебной территории
градостроительными комплексами. Предложено учитывать два вида ограничений – это
временные и топологические, которые в свою очередь разделяются на две группы
абсолютных и относительных ограничений. В содержательном плане под абсолютным
ограничением понимается «жесткая» фиксация конкретного места данного объекта в
общей очередности освоения всех объектов, например, можно зафиксировать, что
для любой очередности, реализующей весь проект, следует начинать со
строительства трансформаторной подстанции. Такая фиксация дает эффект
уменьшения размерности решаемой задачи сразу в N раз, то есть ее размерность
снижается от N! до величины (N-1)! Т.о., эффект от введения абсолютных
ограничений является достаточно существенным, но вместе с этим его реализация
возможна лишь для объектов, фиксируемых, как правило, на первых местах. В этом
отношении более распространенными являются относительные ограничения, которые
устанавливают отношения предшествования объектов. Для градостроительного
комплекса это может быть введение отношения, определяющего, например, то, что
детское дошкольное учреждение может быть построено только после ввода первого жилого
объекта в эксплуатацию. Введение любого бинарного ограничения снижает общую
размерность задачи вдвое для одной пары объектов и более чем вдвое для
нескольких пар объектов. Хотя эффективность сокращения размерности получается
ниже, чем эффект при применении абсолютных ограничений, но количество
относительных ограничений, как правило, больше.
Временные ограничения отражают такие сроки окончаний или начал работ на
объектах, которые не могут быть нарушены. Например, объект не может быть введен
в эксплуатацию раньше, чем состоится поставка оборудования, определенная
договорными сроками. Обобщая подобные ситуации в работе [7] для нахождения оптимума был предложен алгоритм, основанный элиминации
определенных вариантов последовательности освоения энергоресурсосберегающих объектов.
В дальнейшем действие предложенного алгоритма сводилось к перебору всех
очередностей в пределах введенных ограничений, то есть его эффективность
достигнута только за счет снижения размерности задачи.
В работе [8] ставится вопрос о том,
что при планировании долговременной оптимальной очереди, состоящей из
реконструируемых объектов, не учитывается возрастающая во времени неопределенность
их реализации. Экономическая же оценка вариантов очередности одинаково
учитывает изменения эффективности как для объектов, расположенных в начале
очереди, так и для объектов, расположенных в конце очереди. На самом деле
необходимо учитывать феномен, заключающийся в том, что порядок освоения
объектов в планируемой последовательности существенным образом связан с местом
объекта в очереди, а именно, чем раньше запланирована реконструкция объекта,
тем выше его значимость, определяемая большей определенностью. Представленными
в работе [9] результатами
исследованиями установлено, что значимость объекта может рассматриваться как
монотонно убывающая функция.
Рассмотрим предельную эффективность работы
данного алгоритма, которая будет определяться таким резким убыванием значимости
места объекта, при котором следующий выбор объекта не отразится на
предшествующих результатах. В качестве примера критерия может быть взят чистый
дисконтированный доход, который сам по себе представляет собой достаточно
сложную целевую функцию NPV=SNPVj→max, каждый член которой определяется следующим
выражением
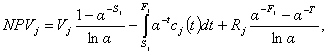 (1)
(1)
где
Vj(t) - функции годовых операционных доходов (расходов) до
проведения
реконструкции на j-м объекте;
Rj(t) - функции годовых операционных доходов (расходов)
после проведения реконструкции на j-м объекте;
Cj(t) - функция инвестиционных затрат в реконструируемый
объект;
Sj и
Fj
- сроки начала и окончания реконструкционных работ на объекте;
Т
- продолжительность выполнения всех реконструкционных работ;
Е=a-1 - норма дисконта, включающая безрисковую
составляющую (ставку),
темп
инфляции и премию за риск инвестиций в комплексный проект.
 Из
формулы (1) следует, что для формирования всех денежных потоков обязательно
необходима разработка соответствующих календарных планов, для формирования
которых также требуется учет трех групп ограничений: топологических, ресурсных
и временных, и это дополнительное обстоятельство делает поставленную задачу еще
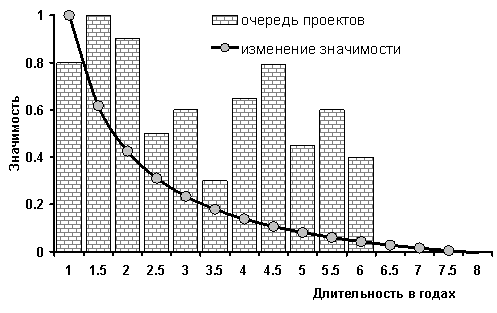
и информационно сложной. Для существенно вогнутой монотонно убывающей функции,
как это показано на рис.1, может быть предложен следующий эвристический
алгоритм оптимизации, получивший название «наискорейшего спуска» в традиционном
«дереве» решений [10].
Из
формулы (1) следует, что для формирования всех денежных потоков обязательно
необходима разработка соответствующих календарных планов, для формирования
которых также требуется учет трех групп ограничений: топологических, ресурсных
и временных, и это дополнительное обстоятельство делает поставленную задачу еще
и информационно сложной. Для существенно вогнутой монотонно убывающей функции,
как это показано на рис.1, может быть предложен следующий эвристический
алгоритм оптимизации, получивший название «наискорейшего спуска» в традиционном
«дереве» решений [10].
Рис.1
Иллюстрация наложения «стоимости времени» на очередность освоения проектов.
На первом шаге оптимизации для всех N
объектов формируются денежные потоки, по
которым определяется объект с максимальным дисконтированным доходом, этот
объект определяется как доминирующий и ставится на первое место. Следующим, из
оставшихся N-1 объектов, по аналогичной схеме определяется
доминирующий объект второй очереди и так далее до полного построения
оптимальной последовательности. На реализацию описанного алгоритма потребуется
расчет N(N-1)/2 вариантов,
что существенно меньше расчета числа вариантов, определяемых факториальной
функцией N!
Другим мероприятием, снижающим
размерность рассматриваемой оптимизационной задачи, является выбор определенного
поточного метода организации строительства с предопределенной целевой функцией.
Так, например, для задачи определения оптимального по времени маршрута
обработки множества деталей на станках с двумя и тремя операциями С.М.Джонсоном
разработан полиномиальный алгоритм оптимизации [11]. Адаптация данной задачи к
поточному строительству была представлена в работе [3] и она заключалась в том,
что под маршрутом понималась последовательность освоения объектов, а под
операциями работы (два или три вида), которые должны выполняться методом
непрерывного использования ресурсов. В практическом плане данный метод обеспечивает
непрерывную работу бригад, при их переходе с объекта на объект.
Суть алгоритма Джонсона
сводится к следующим процедурам: в исходной парной матрице (в качестве примера
взята организация работы двух бригад) отыскивается элемент с наименьшей
продолжительностью и если он находится в левом столбце, то вся строка
перемещается в крайнее верхнее положение, а если в правом – то в крайнее нижнее
положение. Перемещенная строка из дальнейшего рассмотрения исключается, и
процедура повторяется вплоть до полного перестроения исходного маршрута в
оптимальную последовательность, при этом число алгоритмических шагов будет
равно N-1. Несколько отличается алгоритм, предназначенный для
оптимизации с учетом трех видов работ, а для большего числа работ данный
алгоритм вообще не применим. Т.о., полиномиальное решение подобного рода
комбинаторной задачи связано с ограничением на метод организации поточного
строительства, на число работ, отражаемых в расписании и на используемую при
этом целевую функцию, определяющую минимизацию продолжительности строительства
комплекса объектов.
Большую универсальность решению
подобного рода задач дает оптимизационный метод динамического программирования
Беллмана [12]. Однако сам разработчик метода признавал, что на нем лежит
«проклятие размерности». В дополнении к этому для
организационно-технологических задач строительства имеется и другое не менее
существенное ограничение, связанное со свойствами используемой целевой функции.
Дело в том, что она должна быть аддитивной по всем маршрутам освоения объектов
и это обстоятельство делает такую функцию, как чистый дисконтированный доход не
приемлемой.
По сравнению с динамическим
программированием более универсальным является метод «ветвей и границ» [13]. Однако
для этого метода надо иметь дополнительный алгоритм, задачей которого является
определение «нижней» или «верхней» оценки эффективности промежуточных узлов, по
которой определяется перспективность развиваемых «ветвей» решения. К сожалению,
для сложных целевых функций, типа ранее представленной функции (1), разработка
такого алгоритма является само по себе сложным. Если подобного рода алгоритм
оценки точно определил бы эффективную границу множества вариантов, то тогда решенная
задача приблизилась к схеме «наискорейшего спуска», в противном случае решение может
почти в два раза превысить полный перебор всех вариантов.
Считается, что наиболее
универсальными являются различного рода статистические алгоритмы, но они
априори являются приближенными. Однако, на наш взгляд, это не является помехой
в их применении, так как используемая при расчетах целевая функция также объективно
имеет погрешность. В частности, это подтверждается ситуацией, когда для оценки используется
интегральный показатель качества календарного плана работ, в который, как
известно, входят экспертно взвешенные значимости дифференциальных критериев [3,
14]. Поскольку статистические алгоритмы ориентированы на преодоление вычислительной
сложности оптимизационных задач, то результаты их работы базируются не на
генеральной совокупности, а на репрезентативных выборках. Статистический
алгоритм может дать вполне достоверный результат в случае, если окажется, что
погрешность в целевой функции будет больше полученной вариации ее значений, то
есть искомый оптимизационный эффект «утонул» в погрешности целевой функции.
Такой результат может возникнуть в случае оптимизации строительного потока, незначительно
отличающегося от ритмичного потока.
В других же случаях,
представляющих больший интерес, в полученной выборке возможен поиск
определенных закономерностей, нахождению которых посвящена работа [15].
Особенностью данного алгоритма является статистический поиск таких доминантных
фрагментов, которые преимущественно присутствуют в перестановках, предположительно
являющимися близкими к оптимальным перестановкам, и которые выявлены в
результате ранжирования вариантов выборки. Логическая блок-схема такого алгоритма
показана на рис.2.
В описанном алгоритме поиск оптимального решения осуществляется по
интегральному показателю К, который
рассчитывается по следующей формуле
![]() (2)
(2)
где Ki – это
дифференциальный показатель, оценивающий i-ое свойство
календарного плана работ;
Wi – вес
(значимость) дифференциального показателя, определяемый
принятым экспертными методом.
Поскольку вес
каждого показателя несет в себе погрешность, то и интегральный показатель имеет
суммарную погрешность DK, которая в представленный на рис.2 блок-схеме
определяет диапазон оптимальных вариантов.
Во второй итерации процесса работы алгоритма используется информационный
фильтр, полученный на первой стадии его работы. Описанный выше статистический
алгоритм является наиболее универсальными, а связанные с ним негативные
обстоятельства можно исправить с помощью введения дополнительных процедур,
характерных для описанных ниже генетических алгоритмов.
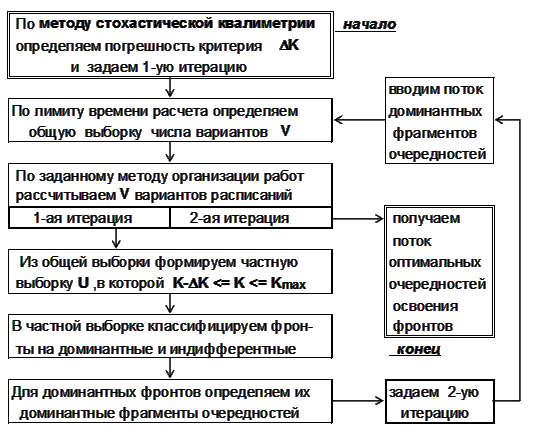

Рис. 2
Блок-схема алгоритма оптимизации, основанного на статистическом поиске
доминантных фрагментов.
Генетическими алгоритмами называются такие эвристические методы поиска
оптимальных решений, которые напоминают биологическую эволюцию, следовательно, данные алгоритмы являются
разновидностью эволюционных вычислений. Отличительная
особенность генетических алгоритмов заключаются в использование операции
«скрещивания», которая производится на множестве пар решений-кандидатов, роль
которых аналогична роли скрещивания в живой природе. «Отцом-основателем»
генетических алгоритмов считается Д. Холланд, изложивший
свои идеи в работе [16]. Общая логическая схема работы различных генетических
алгоритмов показана на рис.3.
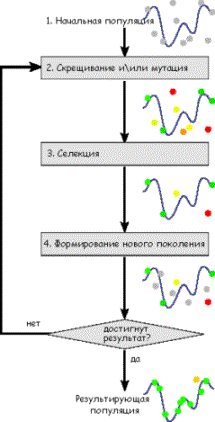
Рис.3. Общая схема реализации генетических
алгоритмов.
Из данного выше
определения следует, что генетические алгоритмы – это адаптивные методы поиска,
которые часто используются для решения задач функциональной оптимизации. Они
основаны на генетических процессах в биологических организмах, в которых
популяции развиваются в течение нескольких поколений, подчиняясь законам естественного
отбора и по принципу «выживает наиболее приспособленный».
Генетические
алгоритмы работают с совокупностью «особей», называемых популяцией, каждая из
которых представляет возможное решение данной проблемы. Обычно генетический
алгоритм генерирует начальную популяцию случайным образом. Каждая особь
оценивается мерой ее «приспособленности» согласно тому, насколько «хорошо»
соответствующее ей решение задачи. Наиболее приспособленные особи получают
возможность «воспроизводить» потомство с помощью «перекрестного скрещивания» с
другими особями популяции. Это приводит к появлению новых особей, которые
сочетают в себе некоторые характеристики, наследуемые ими от родителей.
Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести
потомков, так что те свойства, которыми они обладали, должны исчезнуть из
популяции в процессе эволюции.
Новое поколение должно
содержать более высокое соотношение характеристик, которыми обладают хорошие
члены предыдущего поколения. Поэтому для наиболее приспособленных особей
приводится операция скрещивания, обычно называемая кроссовером и использующая
наиболее перспективные участки генного пространства поиска, при этом считается,
что в конечном итоге, популяция будет сходиться к оптимальному решению задачи. Достижению
эффекта способствуют различные элитные
методы отбора, направляющие эволюцию так, что при отборе обязательно будут
выживать лучшие члены популяции.
При отборе распространена
процедура обязательного сохранения только одной лучшей особи, если она не
прошла как другие через процесс отбора, кроссовера и мутации. Задача исследователей
как раз и заключается в экспериментировании с различными типами представлений, операторов
кроссовера и мутации, при чем логика введения последней операции обычно
сводится к расширению пространства поиска за счет выхода из области локального
экстремума.
Как и все
статистические алгоритмы, данный метод эволюционных вычислений, не гарантирует
обнаружения глобального решения за полиномиальное время, он также не
гарантируют и того, что глобальное решение будет найдено, но он достаточно пригоден
для поиска близкого к оптимальному решению задачи за небольшое приемлемое время.
Главным же преимуществом генетических алгоритмов является то, что они могут
применяться в таких сложных задачах, где не существует других специальных
методов, а если они существуют, то их можно улучшить сочетанием с генетическим
подходом.
Рассмотрим алгоритм
пошагового синтеза генетического
подхода и статистического поиска доминантных фрагментов и логические
основы оптимизации очередности
реконструкции объектов.
0-й шаг. На подготовительном (начальном) этапе задается
целевая функция необходимая для
оценки особей популяции. Это может быть интегральный критерий качества
календарного плана, чистый дисконтированный доход, общее время строительства,
суммарные перерывы между работами и др. Также на данном этапе вводятся
временные и топологические ограничения задач.
1-й шаг. Создается начальная популяция вариантов исходя из половины лимита
времени, выделенного для общего решения задачи. Здесь, как отображено в
блок-схеме рис.2, определены два равновременных оптимизационных этапа,
суммарная продолжительность которых задана лимитом времени.
2-й шаг. Формируется множество элитных вариантов. В соответствии с ранее заданной
целевой функцией и погрешностью в ее исчислении создается множество вариантов,
включающих варианты с минимальными значениями критерия отбора.
3-й шаг. Формируется множество антиэлитных вариантов. В соответствии с ранее
заданной целевой функцией и погрешностью в ее исчислении создается множество
вариантов, включающих варианты с максимальными значениями критерия отбора.
4-й шаг. Формирование элитной популяции. В качестве основы элитной популяции
без изменений принимаются все элитные варианты. В качестве возможного дополнения
к элитным вариантам выбирается множество антиэлитных вариантов, которые
подвергаются направленной мутации, заключающейся в инвертировании мест объектов
в исходных очередностях на противоположные, формируя тем самым кандидатов в
элитную группу.
Введение данной процедуры
связано со следующими обстоятельствами. Описанный выше алгоритм Джонсона
обладает определенной симметрией относительно максимизированного и минимизированного
критериев так, что возникает двойственность, аналогом которой является двойственность
в задачах линейного программирования. Двойственность заключается в том, что
очередность минимизированного оптимального варианта можно инвертировать и
получить максимизированный оптимальный вариант. На этой основе этой эвристики в
алгоритм может быть введена обратная процедура, заключающаяся в получении
оптимального решения на основе инвертирования противоположного решения.
Если инвертированный
антиэлитный вариант является уникальным, то для него рассчитывается целевая
функция, и если ее значение удовлетворяет признаку элитности, то данный вариант
добавляется в элитную популяцию.
5-й шаг. Отбор
элитных генов осуществляется на множестве вариантов элитной популяции. На
данном алгоритмическом шаге используется общая статистика предшествования
объектов в форме матрицы, пример которой показан на рис. 4.
|
Предшествующие объекты |
Последующие
объекты |
||||
|
1-й объект |
2-й объект |
3-й объект |
4-й объект |
5-й объект |
|
|
1-й объект |
|
|
|
|
|
|
2-й объект |
|
|
|
|
|
|
3-й объект |
|
|
|
|
|
|
4-й объект |
|
|
|
|
|
|
5-й объект |
|
|
|
|
|
Рис. 4. Пример статистики
бинарных отношений в обобщенной элитной популяции
Представленная статистика
показывает, какой процент вариантов в обобщенной элитной популяции
соответствует заданному бинарному отношению. Чем этот процент больше отличается
от 50%, тем большая вероятность принадлежности данного отношения к итоговому
доминантному фрагменту, являющемуся признаком оптимального варианта.
Аналогичный показатель, находящийся в районе 50%, с определенной доверительной
вероятностью показывает индифферентные отношения, не входящие в итоговый
доминантный фрагмент. Т.о., наличие определенного бинарного отношения в
доминантном фрагменте может трактоваться как отбор элитных генов из их общей
совокупности.
6-й шаг. Проведение 2-го этапа оптимизации. На основе статистического выбора
доминантных фрагментов производится определение объема новой выборки вариантов
расчета. Если оставшийся лимит времени достаточен для расчета всех новых
вариантов, то алгоритм сводится к их полному перебору, в противном случае число
новых вариантов рассчитывается исходя из лимита времени.
7-й шаг. Окончательный
выбор оптимизированных очередностей освоения объектов осуществляется по
результатам совместной выборки, полученной на обоих этапах расчета.
Следует отметить, что в описании
разработанного алгоритм принята такая степень детализации, которая дала
системный охват его основных логических особенностей, его же дальнейшая
детализация связана с конкретным программным кодом, который в нюансах должен
отражать как специфику решаемой задачи, так и специфику среды программирования.
Резюме. Представленная разработка нового алгоритма ориентирована
на широкий круг задач, связанных с комбинаторной оптимизации календарных планов
организации строительства и производства работ. Полученный алгоритм программно
адаптирован к программе управления проектами Microsoft Project и реализован в ней в виде макроса, что позволяет
автоматизировано решать практические задачи, требующие оптимизационного
подхода.
Литература
1.
Болотин
С.А. Дадар А.Х., Мещанинов И.Ю., Птухина И.С. Методика оптимизационного планирования последовательности
реконструкции энергоресурсосберегающих объектов. В кн. Актуальные проблемы
современного строительства/ СПбГАСУ. В 3 ч. Ч3. СПб. 2011, 199-2-3.
2.
Горбанева Е.П., Мищенко
В.Я. Роль реконструкции и модернизации в системе обеспечения сохранности и
воспроизводства объектов недвижимости// Научный вестник ВГАСУ. Серия:
Дорожно-транспортное строительство. – Воронеж, 2004. – №3. – С.72-76.
3.
Афанасьев В. А. Поточная
организация строительства. – Ленинград, Стройиздат, 1990. 160с.
4.
Юдин Д.Б., Юдин А.Д. Математики
измеряют сложность. М.: Знание, 1985.-192 с.
5.
Болотин С.А., Мещанинов
И.Ю. Основы постановки частной задачи комбинаторной
оптимизации строительства комплекса объектов.//Изв. Вузов.
Строительство. –Новосибирск, -2009. -№2 (602). –С.38-42.
6.
Болотин
С.А., Александрова В.Ф. Анализ порядка освоения объектов при проектировании
календарных планов застройки градостроительными комплексами//Современные
способы организации и управления строительством. Л.: ЛИСИ, 1986.-с.27-30.
7.
Болотин
С.А., Дадар А.Х., Мещанинов И.Ю., Оолакай З.Х Элиминация последовательности
энергоресурсосберегающей реконструкции объектов при учете разнородных
ограничений для нахождения оптимума. Вестник СПбГАСУ, № 3(28), 2011, СС. 60-65.
8.
Болотин С.А., Дадар А.Х.
Оптимизация последовательности реконструкции энергоресурсосберегающих объектов
в условиях роста неопределенности.// Недвижимость:
экономика, управление, 2011, №. – сс.
9.
Теплова Т.В. Динамика
рисков на финансовых рынках и нестандартные модели обоснования затрат на
собственный капитал.//Финансовый менеджмент, 2005.
10.
Лопатников Л.И. Краткий
экономико-математический словарь. М.: Наука, 1979.
11.
Джонсон С.М.
Оптимальные двух- и трехоперационные календарные планы производства с учетом
подготовительно-заключительного времени//Календарное планирование. -М.:
Прогресс, 1966. -с.33-41.
12.
Беллман Р.
,Дрейфус С. Прикладные задачи динамического программирования. -М.: Наука,
1965.-460 с.
13.
Кофман Э.Г.
Теория расписаний и вычислительные машины. М.: Наука, 1984.-335 с.
14.
Болотин
С.А. Дадар А.Х. Определение
погрешности квалиметрической оценки весов аддитивных показателей качества
календарных планов строительства//Изв. вуз. Строительство, № 2, 2010. СС. 29-33.
15. Болотин С.А.
Комбинаторная оптимизация расписаний СМР на основе статистического выявления
доминантных фрагментов.// Деп. ВНИИС Госстроя СССР, №10588, 1990. - 55 с.
16. J. H. Holland.
Adaptation in natural and artificial systems. University of Michigan Press, Ann
Arbor, 1975.