С. А. Оганисян

Государственный инженерный университет Армении

Анализ устойчивости системы управления объектом с четырьмя резервуарами

В работе дано исследование устойчивости системы управления объектом с четырьмя резервуарами [1] с использованием теории количественной обратной связи [2, 3].

Система управления объектом с четырьмя резервуарами представляет собой многомерную систему, созданную К. Х. Йохансоном. Она состоит из четырех взаимосвязанных резервуаров для воды и двух насосов (рис. 1). Целью здесь является контроль уровней двух нижных резервуаров с двумя насосами.

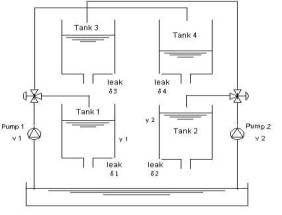
Рис. 1 Система управления объектом с четырьмя резервуарами

Теория количественной обратной связи (КОС), предложенная И. Горовицем, является частотным методом, с помощью которого можно обеспечить требуемые значения качества системы при существовании в ней параметрических неопределенностей.

Рассмотрим систему на рис. 1, представляющую собой двумерную систему, матричная структурная схема которой представлена на рис. 2. Позиция клапанов определяет местоположение многомерного нуля для линеаризованной модели. Нуль можно находиться в левой или правой плоскостях. Таким образом, система может иметь минимальные или неминимальные фазовые характеристики. Мы будем рассматривать систему с минимальной фазовой характеристикой.

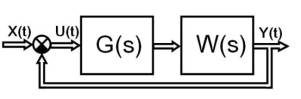
Рис. 2 Общая структурная схема линеаризованной системы

На рис. 2: , и - двумерные векторы входа, ошибки и выхода, - передаточная матрица скалярного регулятора, - передаточная матрица линеаризованного объекта регулирования.

Будем считать, что матрица неопределена и имеет вид:

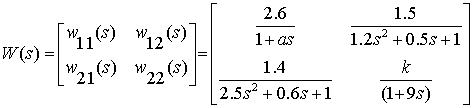, (1)

где параметры и могут принимать значения в следующих интервалах: :

Ставится следующая задача: при неопределенной передаточной матрице (1) выбрать регулятор системы так, чтобы система была устойчивой, а её показатель колебательности по отношению к вектору выхода не превышал значение .

Для применения класической теории КОС к многомерной системе воспользуемся методом характеристических передаточных функций (ХПФ) [4]. Согласно методу ХПФ, передаточная матрица (1) можно представить в следующем каноническом виде:

, (2)

где через обозначены ХПФ разомкнутой системы, а модальная матрица составлена из линейно-независимых собственных векторов матрицы . С помощью ХПФ -мерная система может быть представлена как совокупность независимых одномерных систем, к которым можно применить теорию КОС с использованием диаграмм Найквиста.

В качестве номинальной передаточной матрицы объекта выберем

. (3)

Для решения данной задачи на диаграмме Найквиста построим запретную окружность для заданного значения и характеристические годографы номинальной разомкнутой системы с неопределенностями (рис. 3). Для устойчивости системы необходимо, чтобы годографы не охватывали критическую точку (-1, j0) и находились вне запретной окружности . Из рис. 3 видно, что исходная система неустойчива.

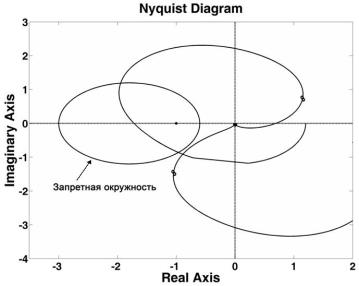
Рис. 3 Характеристические годографы исходной системы

Для обеспечения устойчивости и показателей качества вводим в систему регулятор , передаточная матрица которого имеет следующий вид:

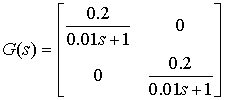. (4)

На рис. 4 показаны характеристические годографы скорректированной системы и запретная окружность для . Как видно из рис. 4, после введения регулятора взаимосвязанная двумерная система стала устойчивой, а ее показатель колебательности не превышает требуемое значение .

Следовательно, можно сделать вывод, что выбранный диагональный регулятор (4) обеспечивает устойчивость и требуемые показатели качества замкнутой системы при заданных параметрических неопределенностях. Рассмотренный подход применим к многомерным системам любой размерности.

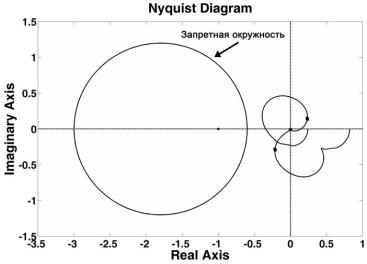
Рис. 4 Характеристические годографы скорректированной системы и

запретная окружность на плоскости диаграммы Найквиста

Литература

1. K. H. Johansson, The Quadruple-Tank Process: A Multivariable Laboratory Process with an Adjustable Zero, pp 456-465, IEEE transaction on control system Technology, vol. 8, No. 3, may 2000.

2. Isaac Horowitz, Invited paper Survey of quantitative feedback theory (QFT), INT.J, CONTROL, 1991, vol. 53, No. 2, 255-291.

3. Constantine H. Houpis, Steven J. Rasmussen, Quantitative feedback theory: fundamentals and applications, 1999 by Marcel Dekker, Inc.

4. Гаспарян О.Н., Теория многосвязных систем автоматического регулирования, ГИУА, Изд.-во “Асогик”, Ереван, 2010.