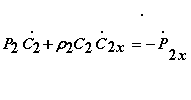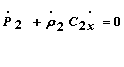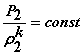УДК 621.515
С. Т. Рахманова, М. М. Шакирьянов,
канд. техн. наук
Классификация упрощенных
моделей газодинамической устойчивости
компрессора как объекта регулирования
Рассматривается обобщение математических моделей
газодинамической устойчивости компрессора. Она дает возможность выбора
алгоритма для последующей разработки электронного автоматического устройства
и(или) соответствующих систем.
Согласно представлениям
о помпажных явлениях первопричиной помпажа является срыв потока с лопаточных
венцов компрессора. При этом наблюдаются низкочастотные колебания давления и
расхода воздуха в газовоздушном тракте.
После резкого падения давления происходит восстановление его первоначальных
значений через десятые доли секунды, а затем весь процесс повторяется снова.
Основной вопрос здесь -
не только построение математических моделей помпажных явлений с помощью
соответствующих преобразований известных уравнений, но и выявление новых,
дополнительных причин (аналитических закономерностей), приводящих к появлению неустойчивых
режимов работы авиационных двигателей[1].
Уравнения движения
газовой системы как многомерного объекта представляются в форме вход – выход,
т.е. с перекрестными связями, когда изменение регулируемой координаты(например,
полной энергии Wn) зависит от изменения всех его управляющих(входных)
координат. Тогда для одномерной САУ, имеющей n регулируемых координат и n регулирующих органов, уравнения
движения системы запишем в следующем виде(см.рис.1):
X(S)=W(S)U(S)+Q(S)F(S)
F(S)
![]()

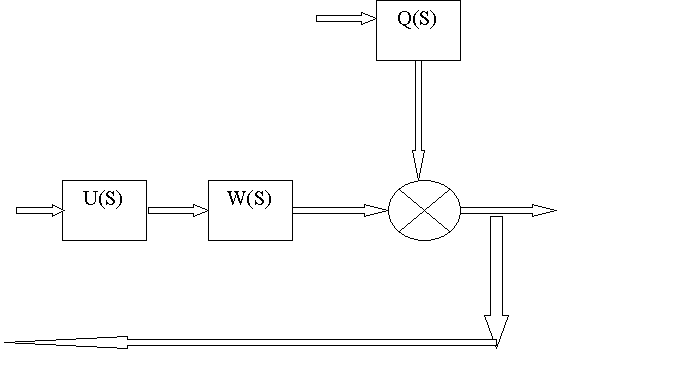

Рис.1 Система
компрессора как объекта регулирования
Где F(S),Q(S) – векторы задающих
координат(например, потенциальной энергии), U(S), W(S) – векторы задающих
координат(например, кинетической энергии), X(S), E(S) – управляющие воздействия(например,
по расходу воздуха, топлива и т.д.).
Классификация является
удобным инструментом для изучения предлагаемых разработок. Она позволяет
тщательно исследовать на предмет применимости тех или иных технических решений.
Классификация
имитационных моделей газодинамической устойчивости компрессора как объекта регулирования
|
Модели,
содержащие акустические параметры |
Модели,
содержащие реальные параметры ГТД |
|
|
Wni=0.5maixi2, mai=rili/s, Wni=maiciViliti. Рассматривается
равенство величин энергий между частями элементов ГТД. Wki+Wni=Wk(i+1)+Wn(i+1). Или 1004,5T1*(pkI0,286-1)+ma1(1,05cVlt+x12/2g)=
1004,5T2*(pkII0,286-1)+ma2(1,05cVlt+x22/2g |
С сосредоточенными параметрами СУЛА Рассматривается
неустой-чивость вокруг равновес-ного режима
+ - |
С распределенными параметрами СУЛА Уравнения(гидродинамики)
Находятся взаимозависи-мые параметры как друг от
друга, так и от времени. Ищутся
выражения и формулы вида
|
В табл. предложены трое видов путей
разработки имитационных математических моделей компрессоров как объектов
управления[2,3].
В первой графе представлены модели,
содержащие акустические параметры двигателя. Здесь Wki — кинетическая энергия газа, заполняющего
участок трубы ГТД, ![]() — амплитуда объемной
скорости, mai — акустическая масса, ri — плотность, li — длина,
Vi — объем, t — время, S —площадь поперечного сечения.
Алгоритмы неустойчивости могут быть получены рассмотрением равенства величин
полных энергий Wki +Wni и Wk(n+1) +Wn(n+1) различных частей СУЛА.
— амплитуда объемной
скорости, mai — акустическая масса, ri — плотность, li — длина,
Vi — объем, t — время, S —площадь поперечного сечения.
Алгоритмы неустойчивости могут быть получены рассмотрением равенства величин
полных энергий Wki +Wni и Wk(n+1) +Wn(n+1) различных частей СУЛА.
Вторая графа посвящена разработке моделей, содержащих
реальные параметры ГТД. Она подразделена на две подграфы.
В одной из них
рассматривается модель выделением отклонения расхода воздуха Q
от равновесного режима. Здесь акустические импедансы определяются
следующим образом
SLa=La(n+2)+ La(n+3)+Lanpkn+La(n+1)p k(n+1)
,
SCan=Ca(n+2))+Ca(n+3)+Can
pkn+Ca(n+1)pk(n+1).
коэффициент сопротивления дросселя
Kn+1=2(P2(n+1)
- P2(n))/QB(n+1), где n - номер
рассматриваемого сечения. Далее полученные уравнения решаются относительно Q и
определяются области устойчивости(например, коэффициент при Q – это статическая
устойчивость(помпажный срыв, а коэффициент при производной Q – это динамическая
устойчивость(помпажные колебания). Реализация получающихся алгоритмов и
сравнение их с соответствующими порогами позволят построить различные
устройства и системы.
В другой подграфе
приведены модели, которые получены рассмотрением совокупности уравнений
(гидродинамики) движения, неразрывности, адиабаты. Здесь P2, С2 и r2 - давление, скорость и плотность
воздуха за компрессором, Р2Х, С2Х, r2Х - скорости изменения давления,
скорости и плотности воздуха за компрессором по расстоянию Х. Р2, С2 - скорости изменения давления и
скорости воздуха за компрессором по времени. В конечном счете определяются
взаимозависимые функции, позволяющие найти области помпажа. Здесь h*k, P2 - скорость изменения к.п.д. и давления воздуха за
компрессором, Р2QI(I), Р2QII - скорости изменения давления воздуха
за первой группой ступеней компрессора по его расходу и давления воздуха за
компрессором по его расходу, соответственно. И далее, сравнивая получающиеся
алгоритмы и частные критерии устойчивости
с соответствующими уставочными значениями можно построить системы и
устройства.
Таким образом,
представленная классификация представляет собой практическую ценность,
указывающая возможные пути разработки математических моделей помпажных явлений.
Список литературы
1.
Казакевич В.В. Автоколебания(помпаж) в
компрессорах. М., Машиностроение, 1974, 264с.
2.
Шакирьянов М.М. Решающая таблица по устранению
различных видов газодинамической неустойчивости в системах, содержащих
лопаточные машины. Изв. вузов, Авиационная техника, 2000, №1, С.80.
3.
Грейцер Е.М. Помпаж и вращающийся срыв в осевых
компрессорах. Экспериментальные результаты и сравнение с теорией.
Энергетические машины и установки, 1976, Изд-во “Мир”, с.75.
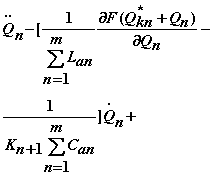
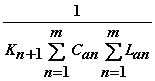
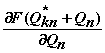 ]Qn=0
]Qn=0